Финансовые данные – получение, особенности и трансформация.
Количественные финансы
Салихов Марсель (marcel.salikhov@gmail.com)
2017-09-16
Цели лекции
- понять, в чем отличия финансовых данных от других типов данных
- изучить основные источники финансовых данных, которые могут быть загружены в R
- получить навыки трансформирования финансовых данных
- изучить особенности расчета доходностей
- разобраться, как и зачем осуществляется корректировка на выплаты дивидендов
- изучить основные особенности финансовых данных с точки зрения статистики
- понять, что такое стационарность временных рядов и почему это важно
Финансовые данные
- Важность количественных методов в бизнесе и финансах увеличивается по мере того, как появляется большее количество информации и данных.
- Финансовые данные систематически собираются в больших количествах и все с большей временной точностью. Достаточно большое количество финансовых данных доступно абсолютно бесплатно.
- Финансовых данных как правило достаточно много по сравнению с другими областями. Вопрос обычно состоит не в том, что данных нет, а в том, чтобы эффективно использовать доступные данные и получить содержательные результаты.
- В R есть множество пакетов, которые позволяют загружать финансовые данные напрямую. Вам не надо заходить куда-то в интернете, скачивать/экспортировать данные, сохранять их на свой компьютер, разбираться форматом хранения, загружать и проч. Обычно загрузка серии – это одна строка кода.
- Основной пакет, который мы будем использовать для получения зарубежных данных финансовых серий –
quantmod, для российских данных – QuantTools (данные ФИНАМа).
- Источники бесплатных данных по финансовым рынкам – Yahoo Finance, Google Finance, FRED, Quandl, для России – Финам, Банк России, Московская Биржа.
- Источники платных данных по финансовым рынкам – системы Bloomberg, Thomson Reuters. Есть провайдеры данных только по ценам на финансовые активы – CQG, AlgoSeek, QuantQuote и другие.
Модель работы с количественными данными
Получение данных из Quandl
- Сервис
Quandl представляет собой удобный сервис для доступа к разным наборам финансовых/экономических данных “в одном месте”. Существуют как платные, так и бесплатные датасеты.
- Для того, чтобы получать данные с Quandl необходимо зарегестрироваться на сайте и получать свой уникальный ключ доступа (API Key)
require(Quandl)
# Crude Oil Futures, Continuous Contract #31 (CL31)
quandl_api_key("enter-your-api-key-here")# ваш собcтвенный API Key
cl = Quandl("CHRIS/CME_CL31")
построим график полученной серии
## Date Open High Low Last Change Settle Volume
## 1 2017-09-14 NA NA NA NA 0.23 51.05 0
## 2 2017-09-13 NA NA NA NA 0.22 50.82 100
## 3 2017-09-12 NA NA NA NA 0.01 50.60 0
## 4 2017-09-11 NA NA NA NA 0.15 50.61 0
## 5 2017-09-08 NA NA NA NA 0.81 50.46 0
## 6 2017-09-07 NA NA NA NA 0.09 51.27 0
## 7 2017-09-06 NA NA NA NA 0.09 51.18 0
## 8 2017-09-05 NA NA NA NA 0.16 51.09 0
## 9 2017-09-01 NA NA NA NA 0.10 50.93 0
## 10 2017-08-31 NA NA NA NA 1.52 50.83 0
## Previous Day Open Interest
## 1 510
## 2 610
## 3 610
## 4 610
## 5 610
## 6 610
## 7 610
## 8 610
## 9 610
## 10 610
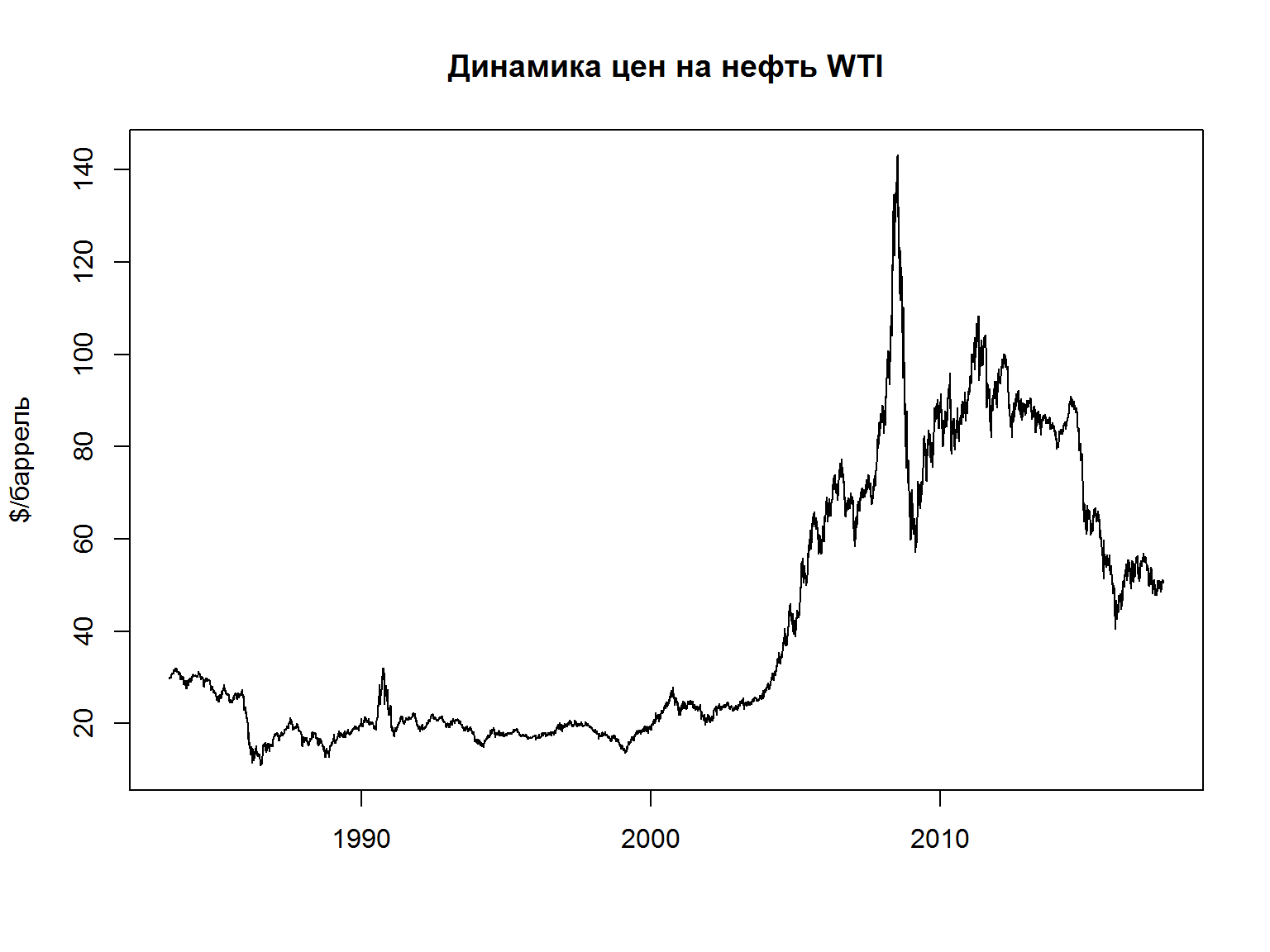
plot(x = cl$Date, y = cl$Settle, type = 'l', ylab ='$/баррель', xlab = "", main = 'Динамика цен на нефть WTI')
Получение данных финансовой отчетности с помощью пакета tidyquant
tidyquant представляет собой еще один пакет, который обеспечивает доступ к данным из разных источников, а также функации для преобразования и визуализации финансовых данных.tidyquant в том числе обеспечивает доступ к данным финансовой отчетности компаний США (источник данных – Google Finance), которая включается в себя (Income Statement, Balance Sheet, and Cash Flow) c разной периодичностью (годовая/annual и квартальная/quarter).
require(tidyquant)
require(dplyr)
aapl_financials <- tq_get("AAPL", get = "financials")
Информация может быть извлечена с помощью функцию пакета `dplyr’.
aapl_financials %>%
unnest(quarter) %>%
spread(key = date, value = value)
## # A tibble: 110 x 8
## type group category `2016-06-25` `2016-09-24`
## * <chr> <int> <chr> <dbl> <dbl>
## 1 BS 1 Cash & Equivalents NA NA
## 2 BS 2 Short Term Investments 52638 58554
## 3 BS 3 Cash and Short Term Investments 61756 67155
## 4 BS 4 Accounts Receivable - Trade, Net 11714 15754
## 5 BS 5 Receivables - Other NA NA
## 6 BS 6 Total Receivables, Net 19042 29299
## 7 BS 7 Total Inventory 1831 2132
## 8 BS 8 Prepaid Expenses NA NA
## 9 BS 9 Other Current Assets, Total 11132 8283
## 10 BS 10 Total Current Assets 93761 106869
## # ... with 100 more rows, and 3 more variables: `2016-12-31` <dbl>,
## # `2017-04-01` <dbl>, `2017-07-01` <dbl>
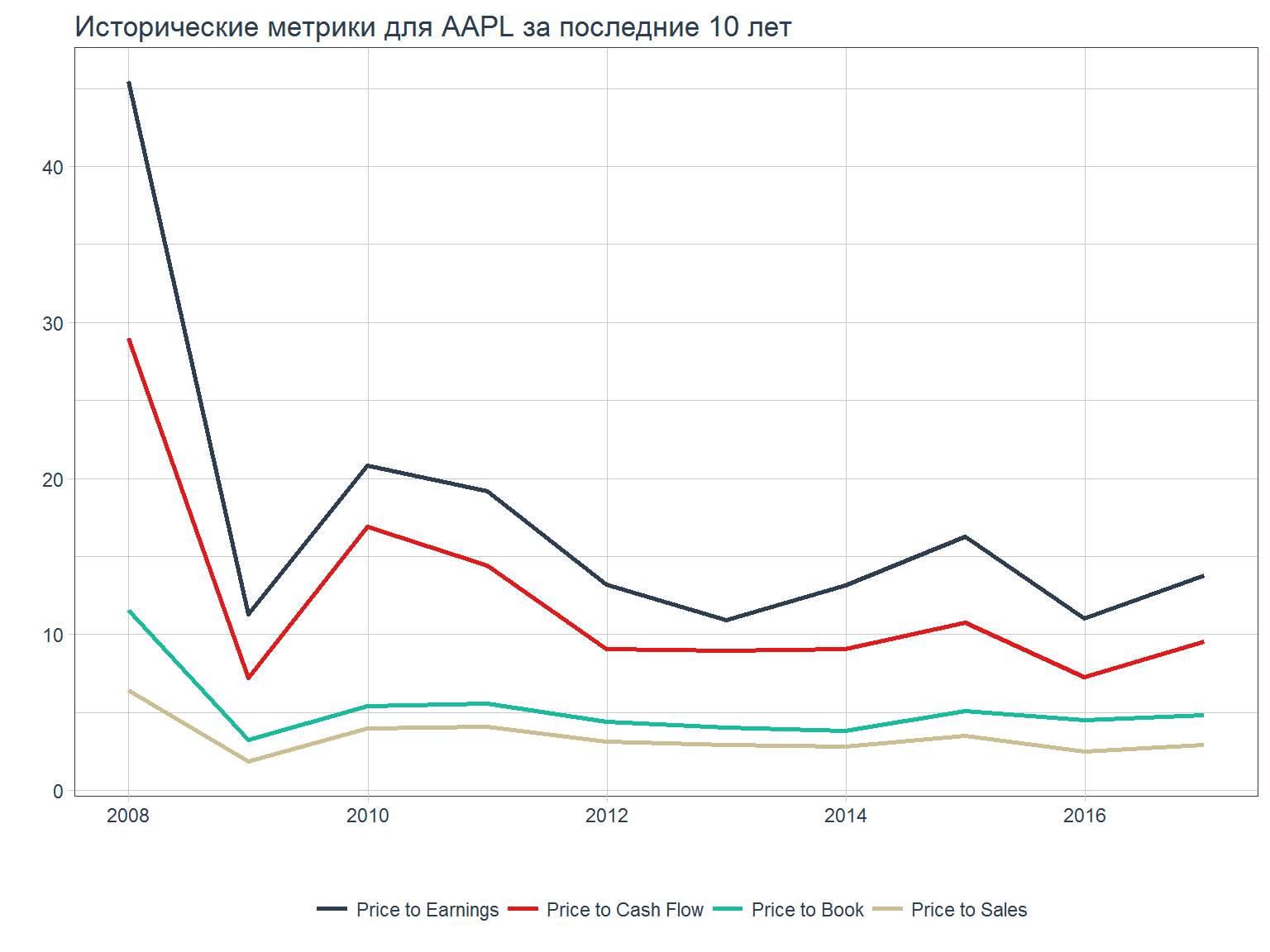
можно также получить данные по ключевой статистике американских эмитентов (источник – Morningstar)
aapl_key_ratios <- tq_get("AAPL", get = "key.ratios")
aapl_key_ratios %>%
dplyr::filter(section == "Valuation Ratios") %>%
unnest() %>%
ggplot(aes(x = date, y = value)) +
geom_line(aes(col = forcats::fct_reorder2(category, date, value)),
size = 1) +
labs(title = "Исторические метрики для AAPL за последние 10 лет", x = "",
y = "", col = "") +
theme_tq() +
scale_color_tq()
Чтение данных из заранее сохраненных файлов
- Формат
.csv является наиболее простым и распространенным вариантам хранения небольших объемов финансовых данных. Файл csv (comma separated values) является просто текстовым файлом, в котором записана таблица данных (обычно использется запятая для того, чтобы разделить данные из разных столбцов)
- В R используются команды
write.csv и read.csv для записи и чтения файлов csv
- У вас также есть возможность читать/записывать данные в формат Excel, но лучше это делать для итогового варианта и не использовать Excel для хранения исходных данных.
- Вы можете подготовить необходимые данные в Excel, экспортировать их в csv, а потом прочитать csv-файл в R.
#write.csv(GSPC, 'data/sp500.csv', row.names = FALSE )
sp500 = read.csv('data/sp500.csv')
# по умолчанию R записывает названия столбцов (row names). если не указано иное, это просто нумерация строк # по порядку - 1,2, 3 и так далее. Нам не нужен столбец, поэтому row.name = FALSE
str(sp500)
## 'data.frame': 17037 obs. of 7 variables:
## $ GSPC.Open : num 16.7 16.9 16.9 17 17.1 ...
## $ GSPC.High : num 16.7 16.9 16.9 17 17.1 ...
## $ GSPC.Low : num 16.7 16.9 16.9 17 17.1 ...
## $ GSPC.Close : num 16.7 16.9 16.9 17 17.1 ...
## $ GSPC.Volume : num 1260000 1890000 2550000 2010000 3850000 2160000 2630000 2970000 3330000 2640000 ...
## $ GSPC.Adjusted: num 16.7 16.9 16.9 17 17.1 ...
## $ date : Factor w/ 17037 levels "1950-01-03","1950-01-04",..: 1 2 3 4 5 6 7 8 9 10 ...
Команда str показывает структуру объекта и указывает, что необходимо изменить формат столбца data из-за того, что он имеет тип factor.
Индекс S&P 500 – долгосрочная динамика фондового рынка
Наиболее простой и популярный тип визуализации финансовых данных – график временного ряда, где по оси Х находятся время, по оси Y – значение
# преобразовать xts в data.frame
data <- sp500[,c('GSPC.Adjusted', 'date')]
data$date <- as.Date(data$date)
# Set up the plot axes, but don't actually plot the data (type = "n")
library(plotly)
plot_ly(data = data, x= ~date) %>%
add_lines(y = ~GSPC.Adjusted)
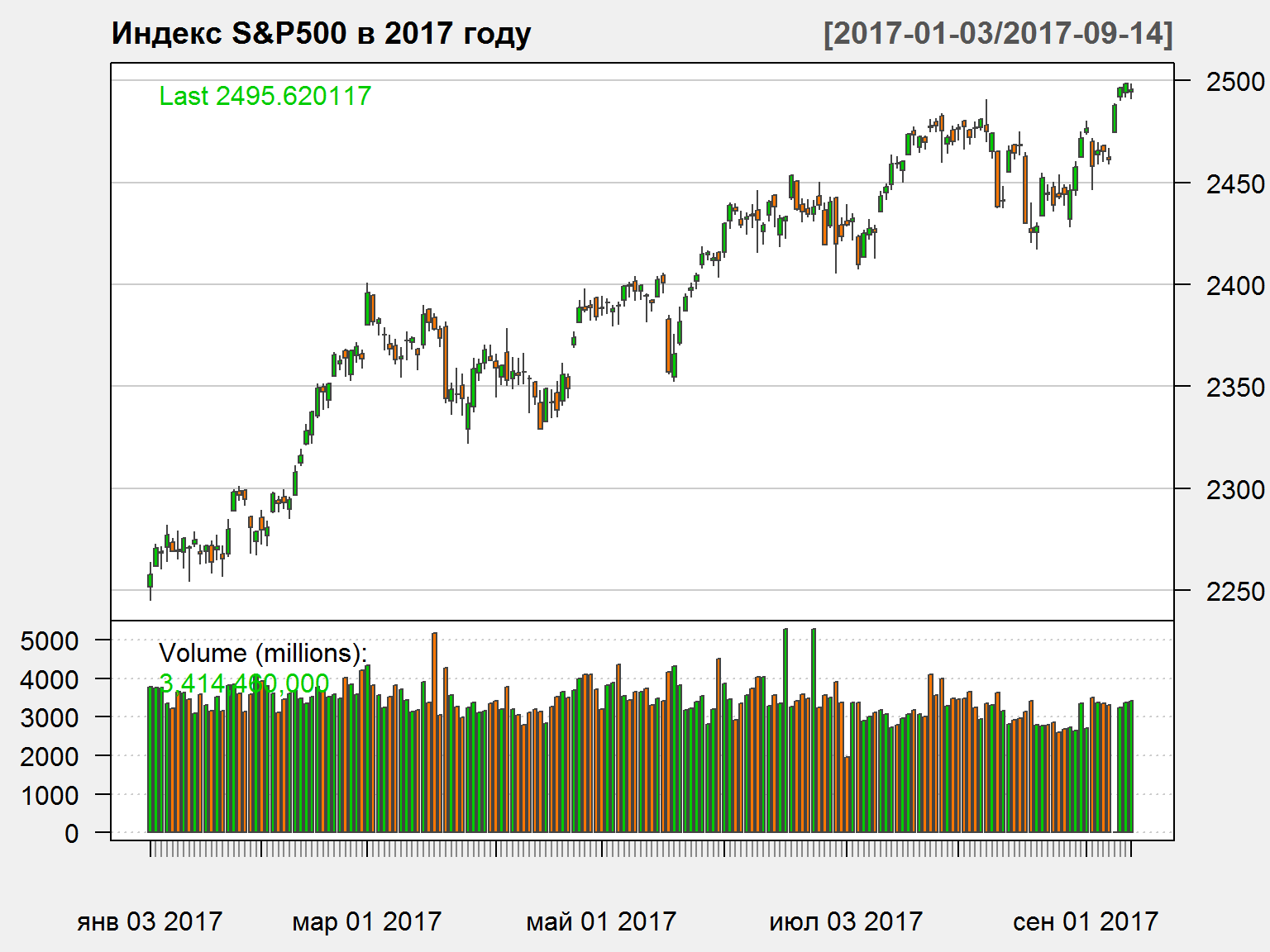
График OHLC
Часто визуальное предоставление финансовых серий осуществляется с помощью графиков OHLC (Open - High - Low - Close)
quantmod::candleChart(GSPC['2017::'], theme = 'white', name = 'Индекс S&P500 в 2017 году')
## GSPC.Open GSPC.High GSPC.Low GSPC.Close GSPC.Volume
## 2017-09-07 2468.06 2468.62 2460.29 2465.10 3353930000
## 2017-09-08 2462.25 2467.11 2459.40 2461.43 3302490000
## 2017-09-11 2474.52 2488.95 2474.52 2488.11 0
## 2017-09-12 2491.94 2496.77 2490.37 2496.48 3230920000
## 2017-09-13 2493.89 2498.37 2492.14 2498.37 3368050000
## 2017-09-14 2494.56 2498.43 2491.35 2495.62 3414460000
## GSPC.Adjusted
## 2017-09-07 2465.10
## 2017-09-08 2461.43
## 2017-09-11 2488.11
## 2017-09-12 2496.48
## 2017-09-13 2498.37
## 2017-09-14 2495.62
Open – цена открытия (начало торгового дня)High – максимальная цена за периодLow – минимальная цена за период
Close – цена закрытияVolume – цена закрытияAdjusted – цена закрытия с учетом корректировок на выплату дивидендов и разделение (split) акций
Вариант графика OHLC – bar chart
barChart(GSPC['2017::'], theme = 'white', name = 'Индекс S&P500 в 2017 году (bar chart)')
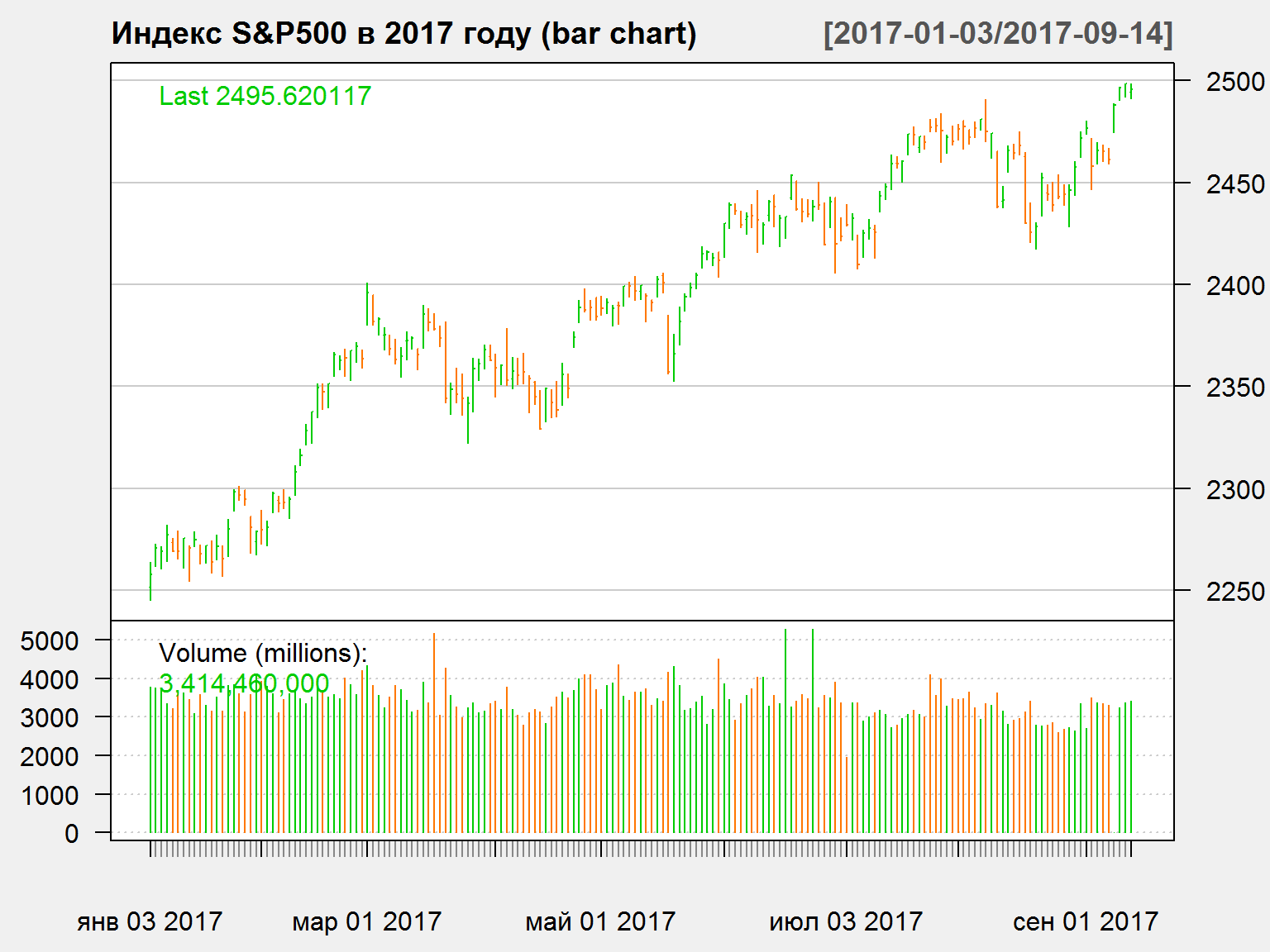
Внутридневные (intraday) данные
- Для дневных серий обычно используют цены закрытия торгового дня (close price). Обратите внимание, что время закрытия для разных торговых площадок может отличаться. Пример – оценка корреляции между ценой на нефть WTI на NYMEX (время закрытия – 21-30 по МСК) и курсом RUB/USD (фиксинг - 12-00 МСК предыдущего дня, время основной сессии на Московской Бирже – c 10-00 до 15-15 и так далее). Эти различия имеют значение на современных рынках.
- Финансовые данные зачастую доступны с очень высоким разрешением – вплоть до мониторинга данных по каждым отдельным торговым операциям (tick data)
- Многие современные финансовые рынки функционируют в круглосуточном режиме. К примеру, валютные рынки устроены подобным образом.
- Скорость обработки информации за последние 10-15 лет выросла драматическим образом. Поэтому реакция рынки на те или иные события очень быстрая. Использование дневных данных не позволяет оценивать эти эффекты.
- Как правило, у вас нет ограничений использовать только дневные данные, внутридневные данные доступны в специализированных системах и базах данных, иногда – бесплатно.
- Внутридневные данные занимают много места и требуют много вычислительных ресурсов для обработки.
Торговля RUB/USD на прошлой неделе - данные за каждые 15 минут
- Используем пакет QuantTools для доступа к данным валютной секции ММВБ
Sys.Date() – это текущая дата (то есть, сегодня), Sys.Date()-5 – это пять дней назад.
## Loading required package: QuantTools
## Loading required package: data.table
##
## Attaching package: 'data.table'
## The following objects are masked from 'package:dplyr':
##
## between, first, last
## The following object is masked from 'package:purrr':
##
## transpose
## The following objects are masked from 'package:xts':
##
## first, last
## The following objects are masked from 'package:lubridate':
##
## hour, isoweek, mday, minute, month, quarter, second, wday,
## week, yday, year
rub = get_finam_data('USDRUB', from = Sys.Date()-5, to = Sys.Date(), period = "15min")
rub = quant_tools_to_xts(rub)
quantmod::candleChart(rub, theme='white', name = 'Динамика торгов долларом США на прошлой неделе')
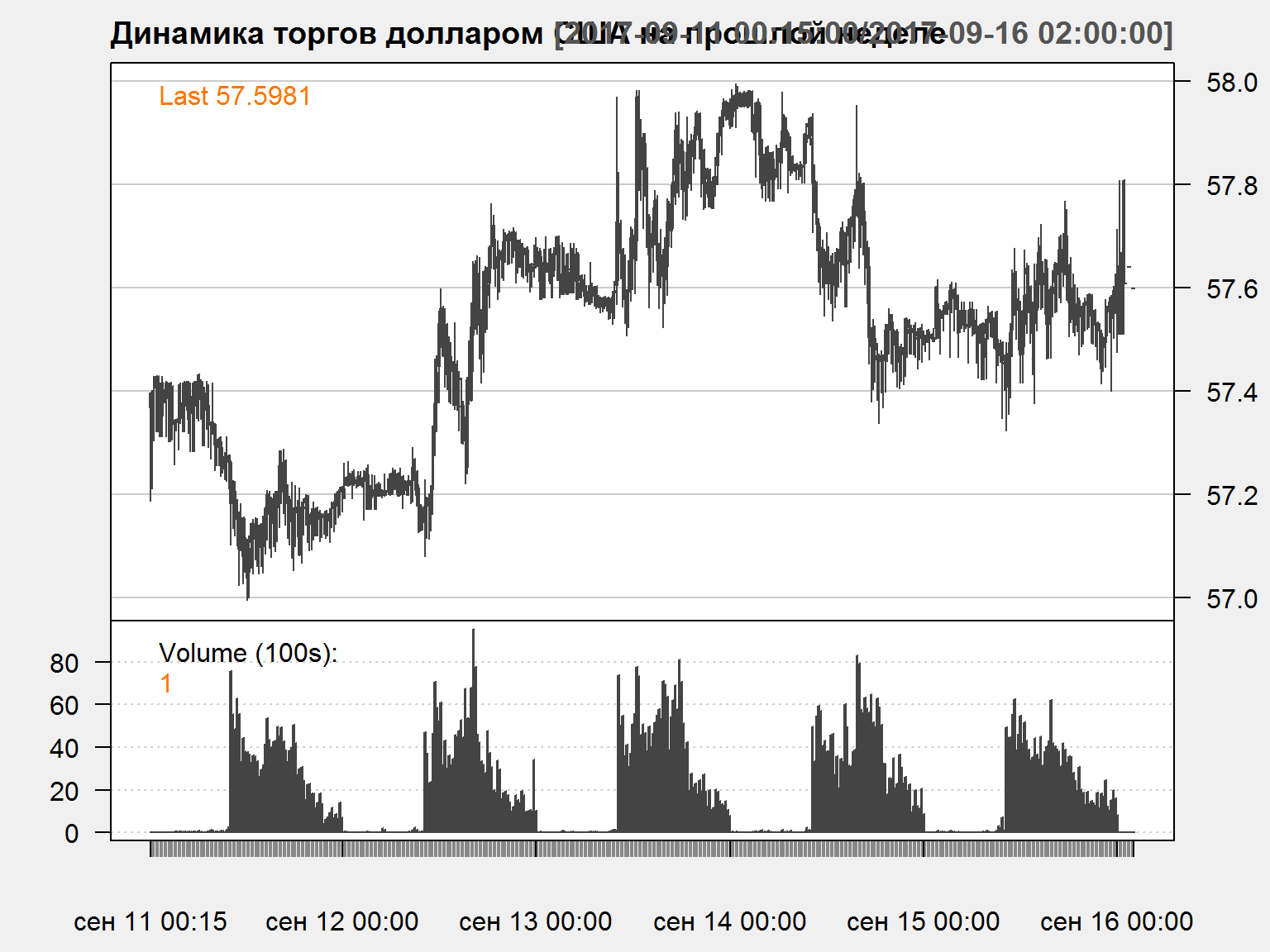
Преобразование данных – изменение периодичности
Чаще все в рамках построения финансовых моделей мы не работаем не с исходными данными непосредственно, а осуществляем преобразования данных для того, чтобы привести их в нужную форму. Преобразования могут быть следующими:
- Переход от дневных к месячным/недельным данным или от внутридневных данных – к дневным. Можно перейти от данных меньшей размерности – к большей, но не наоборот. То есть, к примеру, невозможно перейти от недельных данных – к дневным.
- Функции
to.xxx из пакета xts позволяют легко осуществлять подобные преобразования. Для данных OHLC функция осуществляет корректный расчет максимальных/минимальных значений за период, а также величины объемы торгов (столбец Volume)
periodicity(GSPC) # исходная перодичность данных
## Daily periodicity from 1950-01-03 to 2017-09-14
## GSPC.Open GSPC.High GSPC.Low GSPC.Close GSPC.Volume GSPC.Adjusted
## апр 2017 2362.34 2398.16 2328.95 2384.20 65265670000 2384.20
## май 2017 2388.50 2418.71 2352.72 2411.80 79607170000 2411.80
## июн 2017 2415.65 2453.82 2405.70 2423.41 81002490000 2423.41
## июл 2017 2431.39 2484.04 2407.70 2470.30 63169400000 2470.30
## авг 2017 2477.10 2490.87 2417.35 2471.65 70616030000 2471.65
## сен 2017 2474.42 2498.43 2446.55 2495.62 26245250000 2495.62
## GSPC.Open GSPC.High GSPC.Low GSPC.Close GSPC.Volume GSPC.Adjusted
## 2016 Q2 2056.62 2120.55 1991.68 2098.86 246861290000 2098.86
## 2016 Q3 2099.34 2193.81 2074.02 2168.27 222410800000 2168.27
## 2016 Q4 2164.33 2277.53 2083.79 2238.83 236747630000 2238.83
## 2017 Q1 2251.57 2400.98 2245.13 2362.72 221193370000 2362.72
## 2017 Q2 2362.34 2453.82 2328.95 2423.41 225875330000 2423.41
## 2017 Q3 2431.39 2498.43 2407.70 2495.62 160030680000 2495.62
Преобразование данных – изменение периодичности
- Выбор определенного периода времени для анализа. Объекты типа
xts позволяют осуществлять выборку данных внутри квадратных скобок
head(GSPC['2017']) # весь 2017 год
## GSPC.Open GSPC.High GSPC.Low GSPC.Close GSPC.Volume
## 2017-01-03 2251.57 2263.88 2245.13 2257.83 3770530000
## 2017-01-04 2261.60 2272.82 2261.60 2270.75 3764890000
## 2017-01-05 2268.18 2271.50 2260.45 2269.00 3761820000
## 2017-01-06 2271.14 2282.10 2264.06 2276.98 3339890000
## 2017-01-09 2273.59 2275.49 2268.90 2268.90 3217610000
## 2017-01-10 2269.72 2279.27 2265.27 2268.90 3638790000
## GSPC.Adjusted
## 2017-01-03 2257.83
## 2017-01-04 2270.75
## 2017-01-05 2269.00
## 2017-01-06 2276.98
## 2017-01-09 2268.90
## 2017-01-10 2268.90
tail(GSPC['/2017']) # все по 2017 год
## GSPC.Open GSPC.High GSPC.Low GSPC.Close GSPC.Volume
## 2017-09-07 2468.06 2468.62 2460.29 2465.10 3353930000
## 2017-09-08 2462.25 2467.11 2459.40 2461.43 3302490000
## 2017-09-11 2474.52 2488.95 2474.52 2488.11 0
## 2017-09-12 2491.94 2496.77 2490.37 2496.48 3230920000
## 2017-09-13 2493.89 2498.37 2492.14 2498.37 3368050000
## 2017-09-14 2494.56 2498.43 2491.35 2495.62 3414460000
## GSPC.Adjusted
## 2017-09-07 2465.10
## 2017-09-08 2461.43
## 2017-09-11 2488.11
## 2017-09-12 2496.48
## 2017-09-13 2498.37
## 2017-09-14 2495.62
head(GSPC['2017/2017-03']) # c январь по март 2017 года
## GSPC.Open GSPC.High GSPC.Low GSPC.Close GSPC.Volume
## 2017-01-03 2251.57 2263.88 2245.13 2257.83 3770530000
## 2017-01-04 2261.60 2272.82 2261.60 2270.75 3764890000
## 2017-01-05 2268.18 2271.50 2260.45 2269.00 3761820000
## 2017-01-06 2271.14 2282.10 2264.06 2276.98 3339890000
## 2017-01-09 2273.59 2275.49 2268.90 2268.90 3217610000
## 2017-01-10 2269.72 2279.27 2265.27 2268.90 3638790000
## GSPC.Adjusted
## 2017-01-03 2257.83
## 2017-01-04 2270.75
## 2017-01-05 2269.00
## 2017-01-06 2276.98
## 2017-01-09 2268.90
## 2017-01-10 2268.90
Преобразование данных – первые/последние элементы
- Функции
xts::first и xts::last позволяют вам получить первые или последние элементы объекта xts. Второй аргумент фукнций позволяет задавать количество периодов, которое нам необходимо.
- Названия функций first/last используются в других пакетах, поэтому используется синтаксис
xts::first. Это означает использовать функцию first именно из пакета xts.
xts::last(GSPC, '1 week') ## последняя неделя
## GSPC.Open GSPC.High GSPC.Low GSPC.Close GSPC.Volume
## 2017-09-11 2474.52 2488.95 2474.52 2488.11 0
## 2017-09-12 2491.94 2496.77 2490.37 2496.48 3230920000
## 2017-09-13 2493.89 2498.37 2492.14 2498.37 3368050000
## 2017-09-14 2494.56 2498.43 2491.35 2495.62 3414460000
## GSPC.Adjusted
## 2017-09-11 2488.11
## 2017-09-12 2496.48
## 2017-09-13 2498.37
## 2017-09-14 2495.62
xts::last(GSPC, '3 days') ## последние три дня
## GSPC.Open GSPC.High GSPC.Low GSPC.Close GSPC.Volume
## 2017-09-12 2491.94 2496.77 2490.37 2496.48 3230920000
## 2017-09-13 2493.89 2498.37 2492.14 2498.37 3368050000
## 2017-09-14 2494.56 2498.43 2491.35 2495.62 3414460000
## GSPC.Adjusted
## 2017-09-12 2496.48
## 2017-09-13 2498.37
## 2017-09-14 2495.62
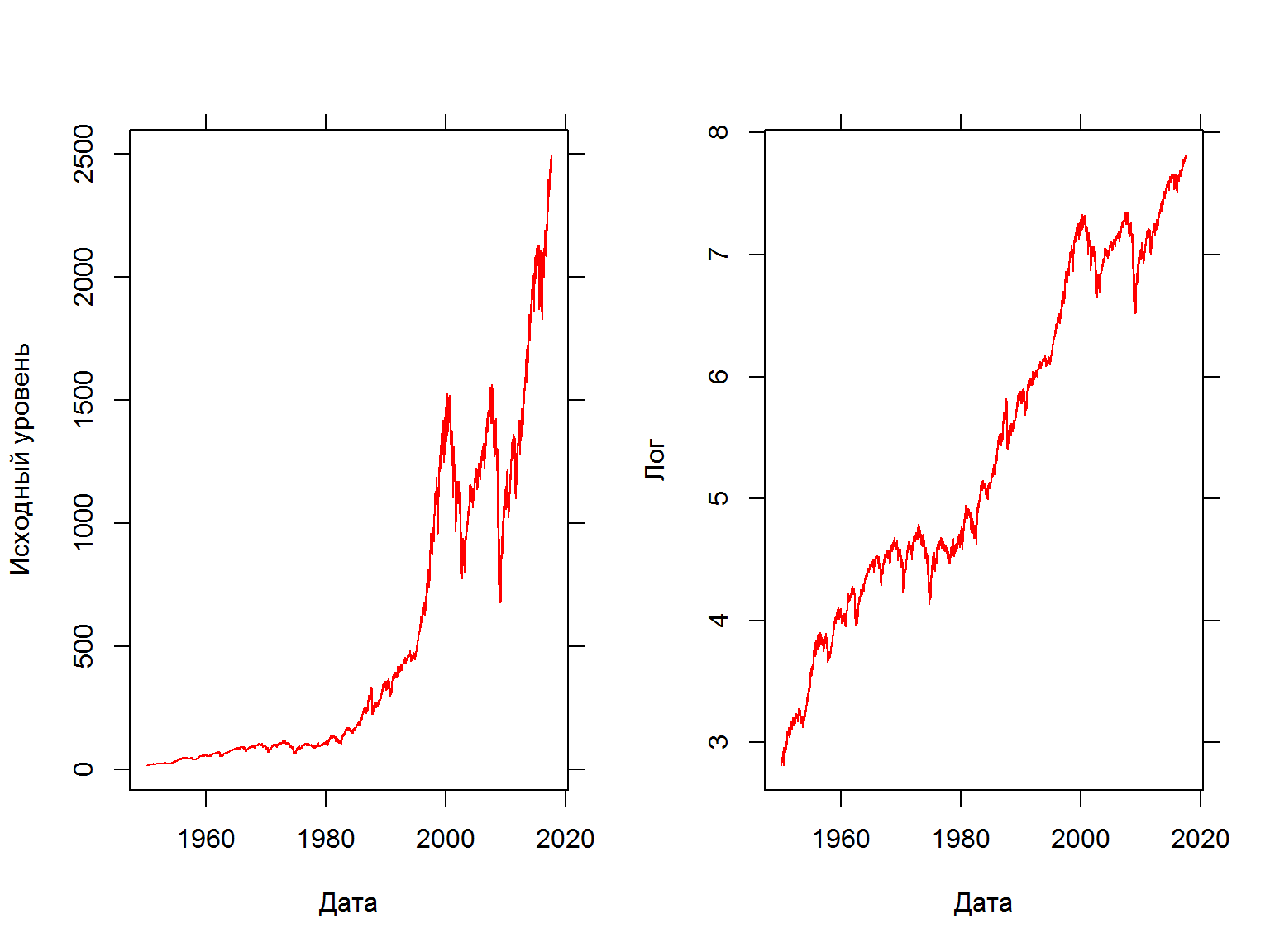
Преобразование данных – логарифм
Используйте лог-преобразование для того, чтобы скорректировать серию на экспоненциальный рост и “ограничить” волатильность.
par(mfrow = c(1,2))
fancy.plot(index(GSPC),GSPC$GSPC.Adjusted, t="l", xlab="Дата", ylab="Исходный уровень", col=2)
fancy.plot(index(GSPC),log(GSPC$GSPC.Adjusted), t="l", xlab="Дата", ylab="Лог", col=2)
Регрессия логарифма S&P по времени
- Посчитаем простую линейную регрессию зависимости абсолютного лог-значения индекса SP500 от времени c помощью функции
lm.
## GSPC.Adjusted date
## 1 16.66 1950-01-03
## 2 16.85 1950-01-04
## 3 16.93 1950-01-05
## 4 16.98 1950-01-06
## 5 17.08 1950-01-09
## 6 17.03 1950-01-10
names(data)[1] <- 'sp500'
data$sp500.log <- log(data$sp500)
time <- 1:nrow(data)
model.time <- lm(data$sp500.log ~ time)
summary(model.time)
##
## Call:
## lm(formula = data$sp500.log ~ time)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.71837 -0.18413 0.00569 0.20039 0.76318
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.103e+00 4.308e-03 720.2 <2e-16 ***
## time 2.742e-04 4.379e-07 626.1 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.2811 on 17035 degrees of freedom
## Multiple R-squared: 0.9584, Adjusted R-squared: 0.9583
## F-statistic: 3.92e+05 on 1 and 17035 DF, p-value: < 2.2e-16
Сравним фактические данные и модельную регрессию:
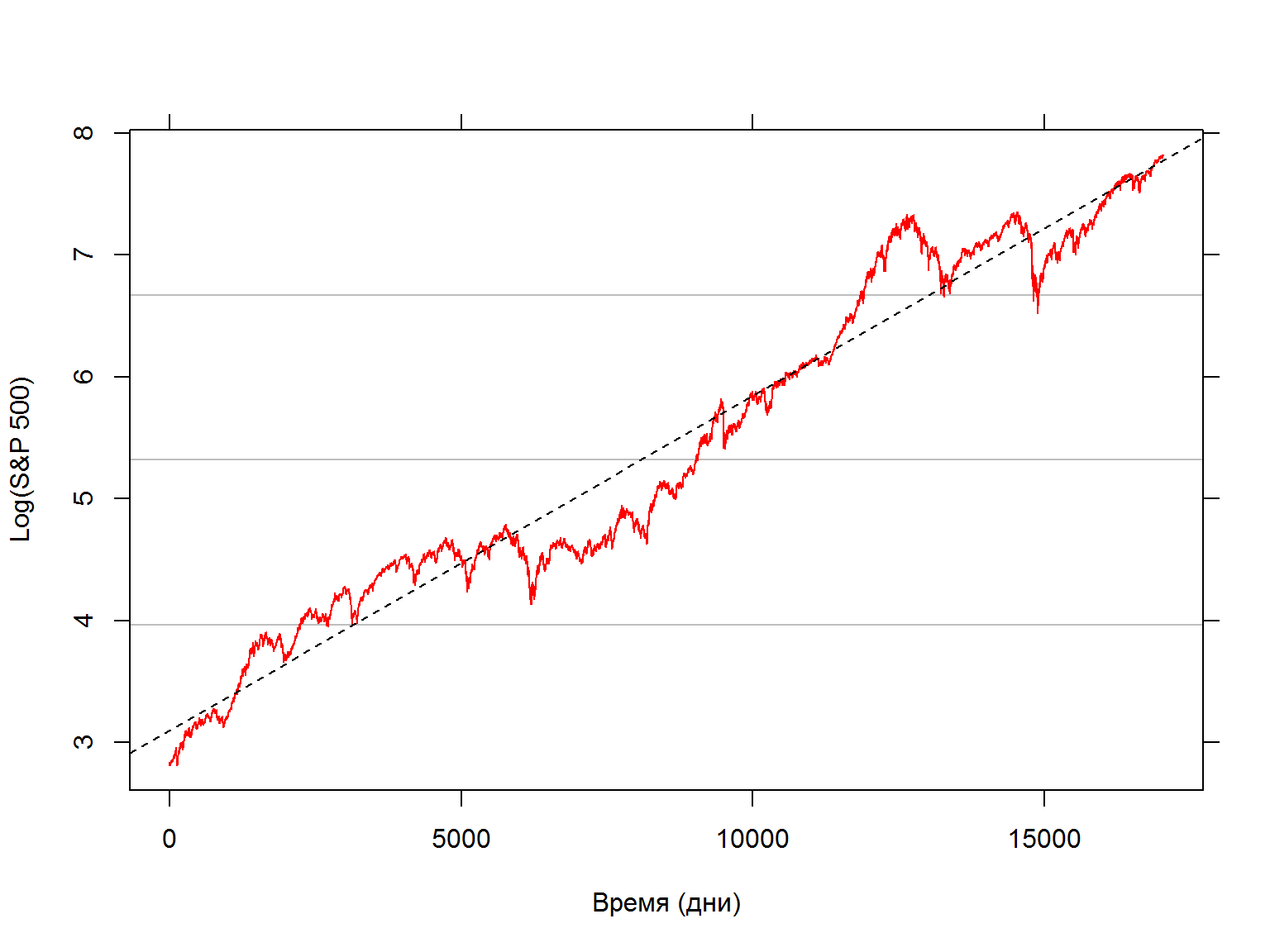
Может ли вчерашнее значение индекса предсказать нам значение сегодня?
data$sp500.lag.log <- c(NA, lag(data$sp500.log)[-nrow(data)])
fancy.plot(data$sp500.lag.log, data$sp500.log, cex=0.5, col=2, xlab="Значение вчера Log(S&P 500)", ylab="Значение сегодня Log(Dow)", asp=1)

Может ли вчерашнее значение индекса предсказать нам значение сегодня? (2)
Посчитаем регрессию
model.yest <- lm(data = data, sp500.log ~ sp500.lag.log)
print(summary(model.yest), digits=6)
##
## Call:
## lm(formula = sp500.log ~ sp500.lag.log, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.28253786 -0.00691331 0.00041678 0.00734109 0.13845283
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.06047e-03 4.32198e-04 2.45367 0.014151 *
## sp500.lag.log 9.99913e-01 7.70421e-05 12978.78642 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.0138493 on 17033 degrees of freedom
## (2 observations deleted due to missingness)
## Multiple R-squared: 0.999899, Adjusted R-squared: 0.999899
## F-statistic: 1.68449e+08 on 1 and 17033 DF, p-value: < 2.22e-16
## 2.5 % 97.5 %
## (Intercept) 0.0002133188 0.001907625
## sp500.lag.log 0.9997620282 1.000064049
Похоже, что не очень. Согласно посчитанной регрессии, “сегодня” будет таким же, как вчера (\(\beta = 1\)).
! В финансовых данных обычно наблюдения, которые находятся “рядом”" другом с другом, скоррелированны между собой.
Гистограмма лог-значений – проверка допущений
Гистограмма указывает на то, что моменты распределения не являются устойчивыми. Использование данных в такой форме (“в уровнях”) не очень осмысленно.
hist(data$sp500.log, breaks=50, col=2, xlab="Log(S&P 500)", main="Гистограмма лог-значений S&P 500")
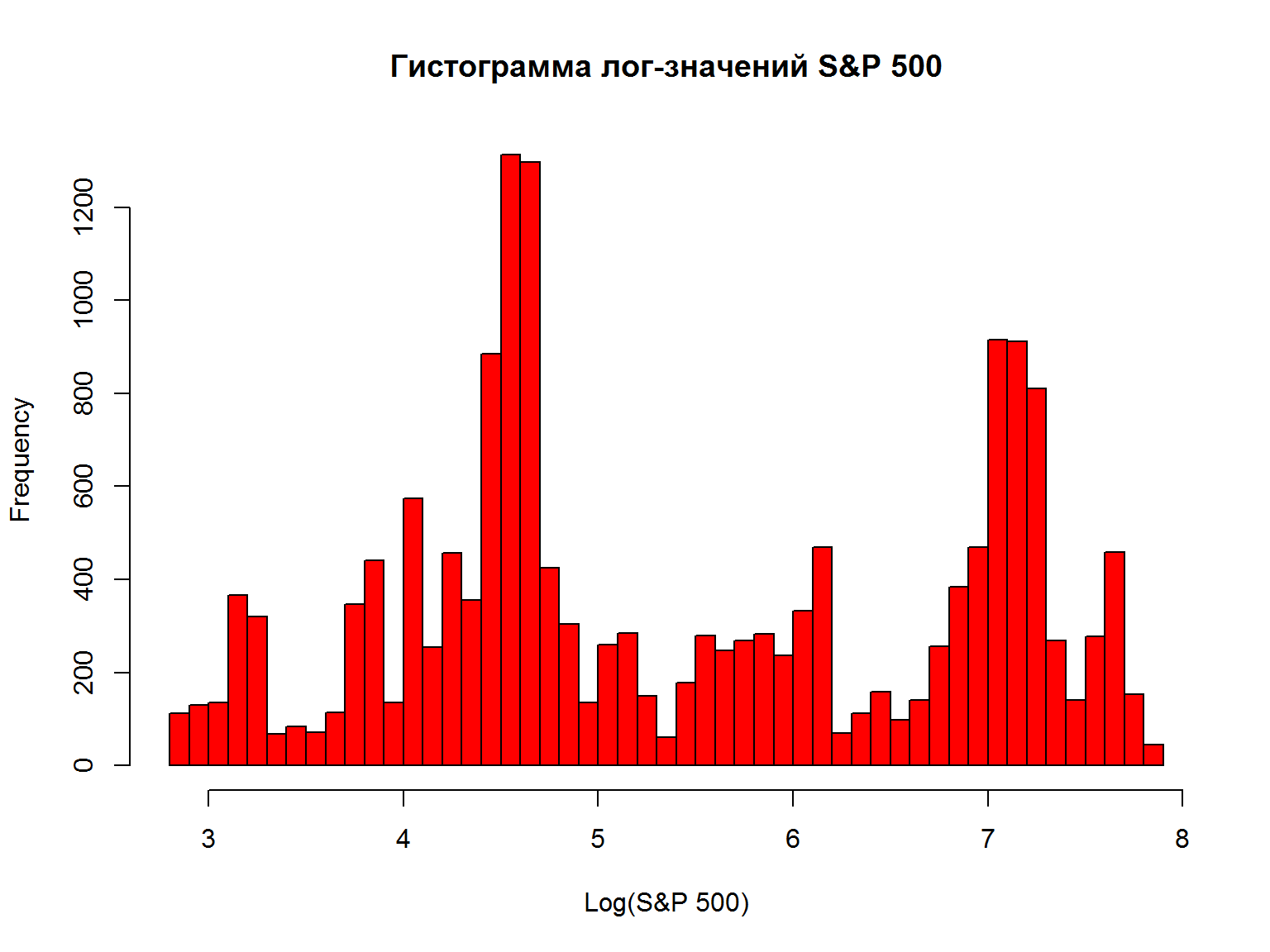
Может быть, надо преобразовать значения серии?
Доходность
Доходность – лог-значение “сегодня” минус лог-значение “вчера” или лог-доходность
data$sp500.ret <- data$sp500.log - data$sp500.lag.log
fancy.plot(data$date, data$sp500.ret, t="l", xlab="Дата", ylab="Лог-доходность", col=2)
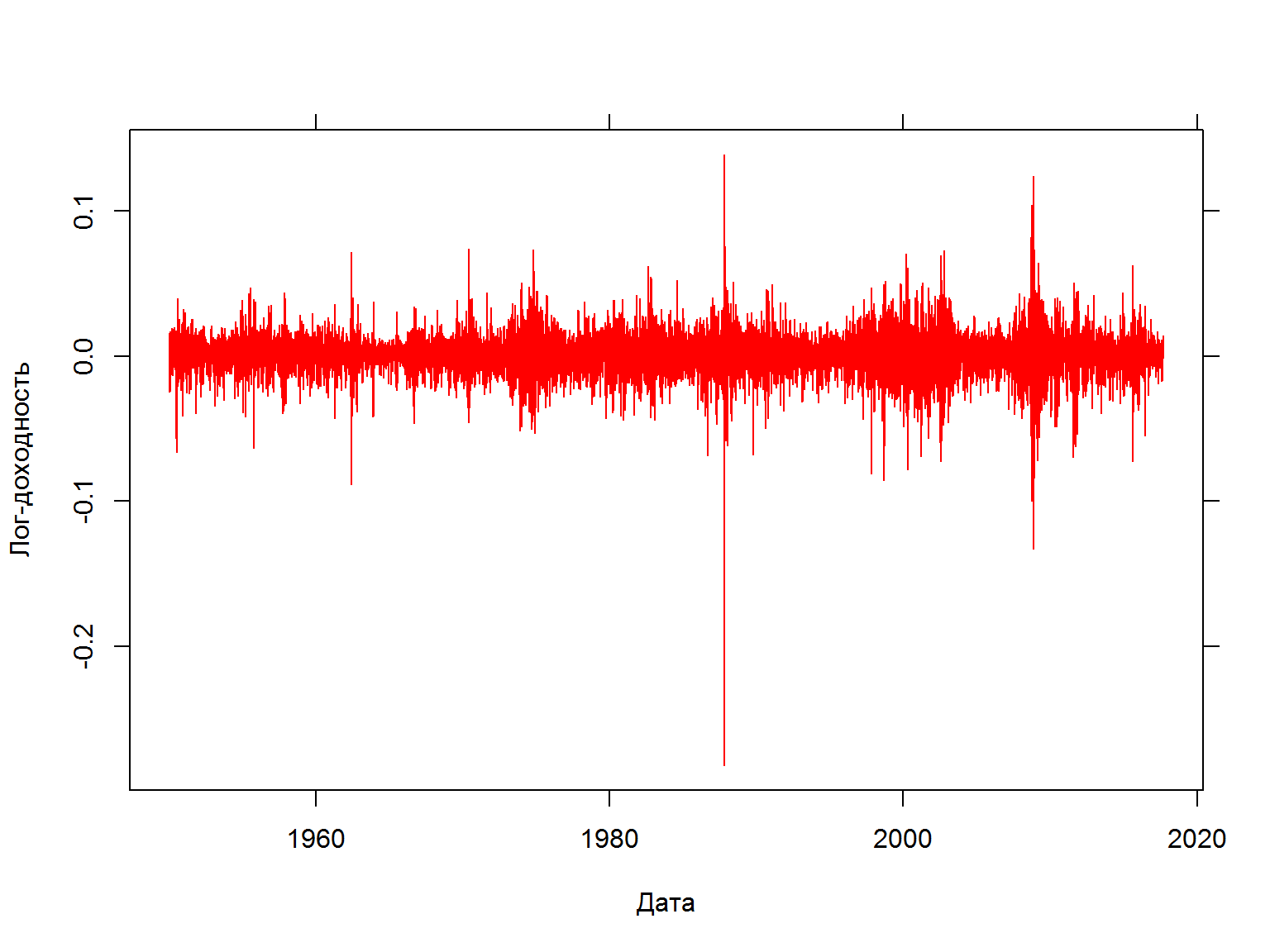
#diff(log(GSPC$GSPC.Close)) - расчет лог-доходности для объектов xts
Нетто-доходность
Пусть \(P_t\) это цена финансового актива в момент времени \(t\). Если мы предположим, что в этот период не было выплат дивидендов, то нетто-доходность за период владения со времени \(t-1\) до времени \(t\) составит
\[ R_t = \frac{P_t}{P_{t-1}} -1 = \frac{P_t - P_{t-1}}{P_{t-1}} \]
Числитель – прибыль, полученная за период владения, отрицательное значение означает убыток.
Знаменатель – первоначальная инвестиция, сделанная в начале периода владения. Минимальное значение доходности = -1, то есть 100% убыток или потеря всей первоначальной инвестиции.
\[ R_t \geq -1 \]
Валовая доходность
Валовая доходность определяется как:
\[ \frac{P_t}{P_{t-1}} = 1 + R_t \]
Доходности не зависят от размерности исходных величин (доллары, рубли и проч.) Размерность доходности – время. Она зависит от единиц \(t\) (час, день, неделя, год).
Валовая доходность за последние \(k\) периодов является произведением доходностей за каждый из периодов:
\[ 1 + R_t(k) = \frac{P_t}{P_{t-k}} = (\,\frac{P_t}{P_{t-1}})\,(\frac{P_{t-1}}{P_{t-2}}) ... (\frac{P_{t-k+1}}{P_{t-k}}) \]
Лог-доходность (continuously compounded return)
Лог-доходность или continuously compounded returns определяются как:
\[ r_t = log(1 + R_t) = log(\frac{P_t}{P_{t-1}}) = p_t - p_{t-1} \]
где \(p_t = log(P_t)\) – лог-цена.
Лог-доходности примерно равны доходностям из-за того, что если \(x\) достаточно малая величина, то \(log(1+x) \approx x\)
retseq <- seq(-.5, .5, length=100)
plot(retseq, log(retseq + 1), type="l",
axes=FALSE, col="blue", lwd=3, xlab="простая доходность", ylab="Лог доходность")
axis(1, at=c(-.5,-0.25, 0, 0.25, .5), label=c("-50%", "-25%", "0%", "25%", "50%"))
axis(2, at=c(-.5,-0.25, 0, 0.25, .5), label=c("-50%", "-25%", "0%", "25%", "50%"))
abline(0,1, lty=2, lwd = 2, col="red")
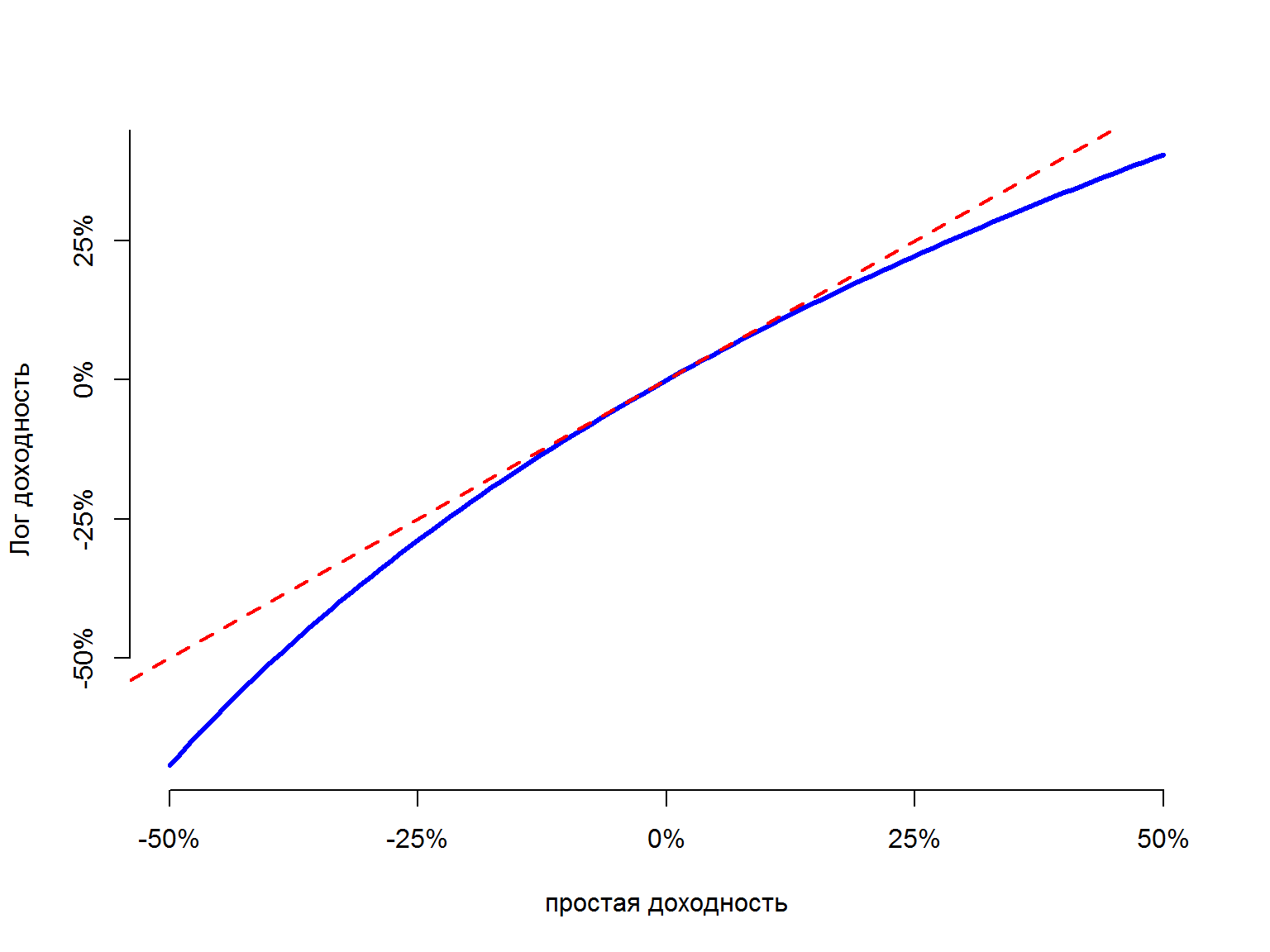
- Чем более короткий промежуток времени (дни, часы, минуты) мы используем, тем меньше будет доходность меньше по абсолютным значениям.Поэтому мы можем ожидать, что доходности будут примерно равно лог-доходностям для дневных и внутридневных данных. Для годовых данных, к примеру, ошибка будет гораздо больше – для них не стоит использовать такое преобразование.
- Доходности и лог-доходности имеют одинаковый знак
- Лог-доходности на всех промежутках значениях больше простой доходности. По мере приближения обычной доходности к -1 (потеря всех инвестиций), лог-доходность стремится к \(-\infty\)
Корректировка на дивиденды для акций
- Многие компании, особенно из традиционных секторов, платят дивиденды, которые должны быть учтены при оценке полной доходности (total return).
- Если мы не учитываем эту компоненту, то мы рискуем неправильно оценивать доходности для инвесторов и исказить результаты анализа.
- Иногда компании проводят разделение акций (stock split), то есть обмен “старых” акций на “новые” в определенном соотношении. К примеру, каждый владелец 1 старой акции получает 2 новых. В этих операциях нет экономической сути, они делаются просто для удобства котирования цен и/или по историческим причинам.
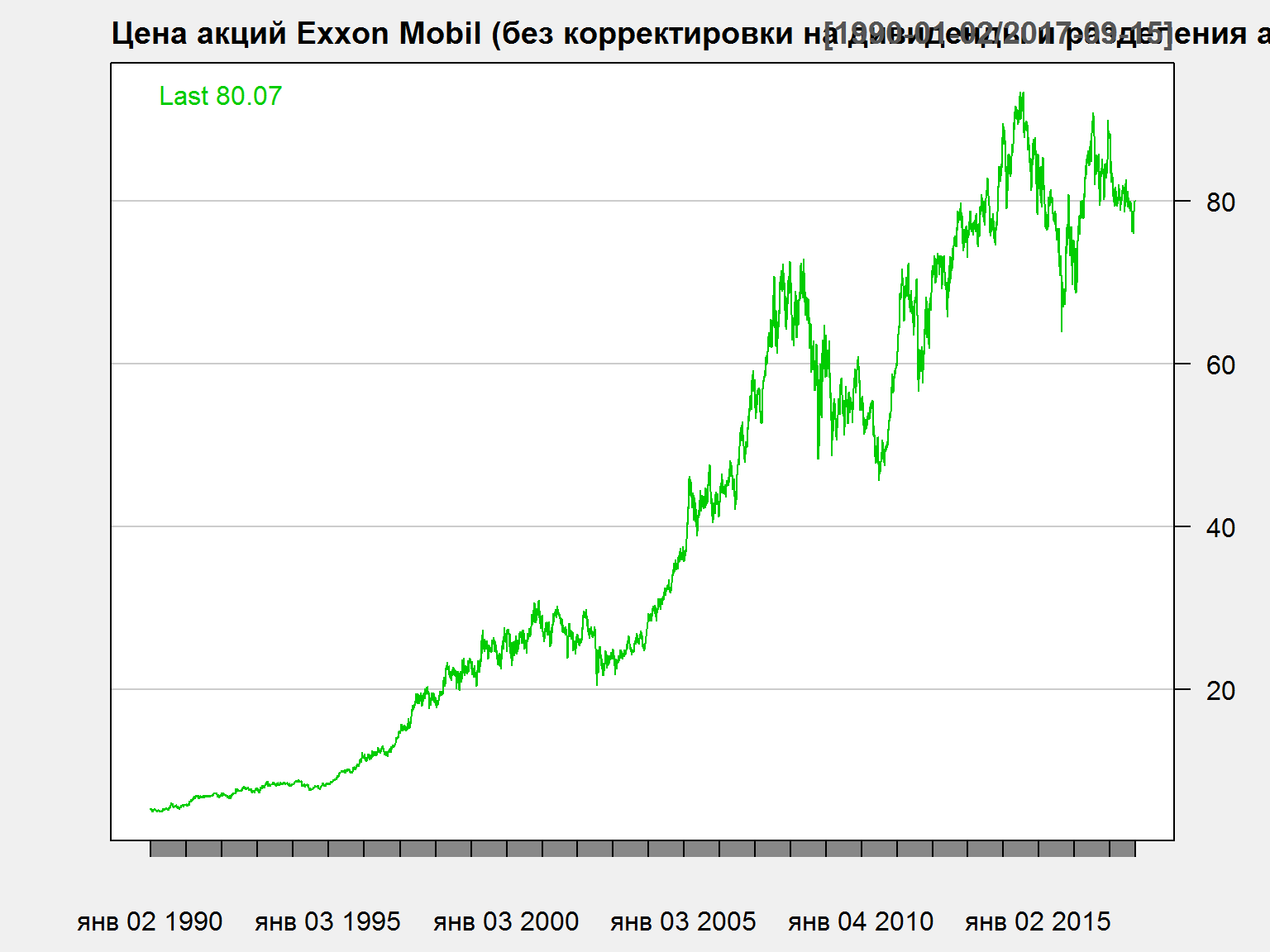
Акции Exxon Mobil - 1
chartSeries(XOM$XOM.Close['1990::'], name = 'Цена акций Exxon Mobil (без корректировки на дивиденды и разделения акций)',multi.col = FALSE, theme = 'white')
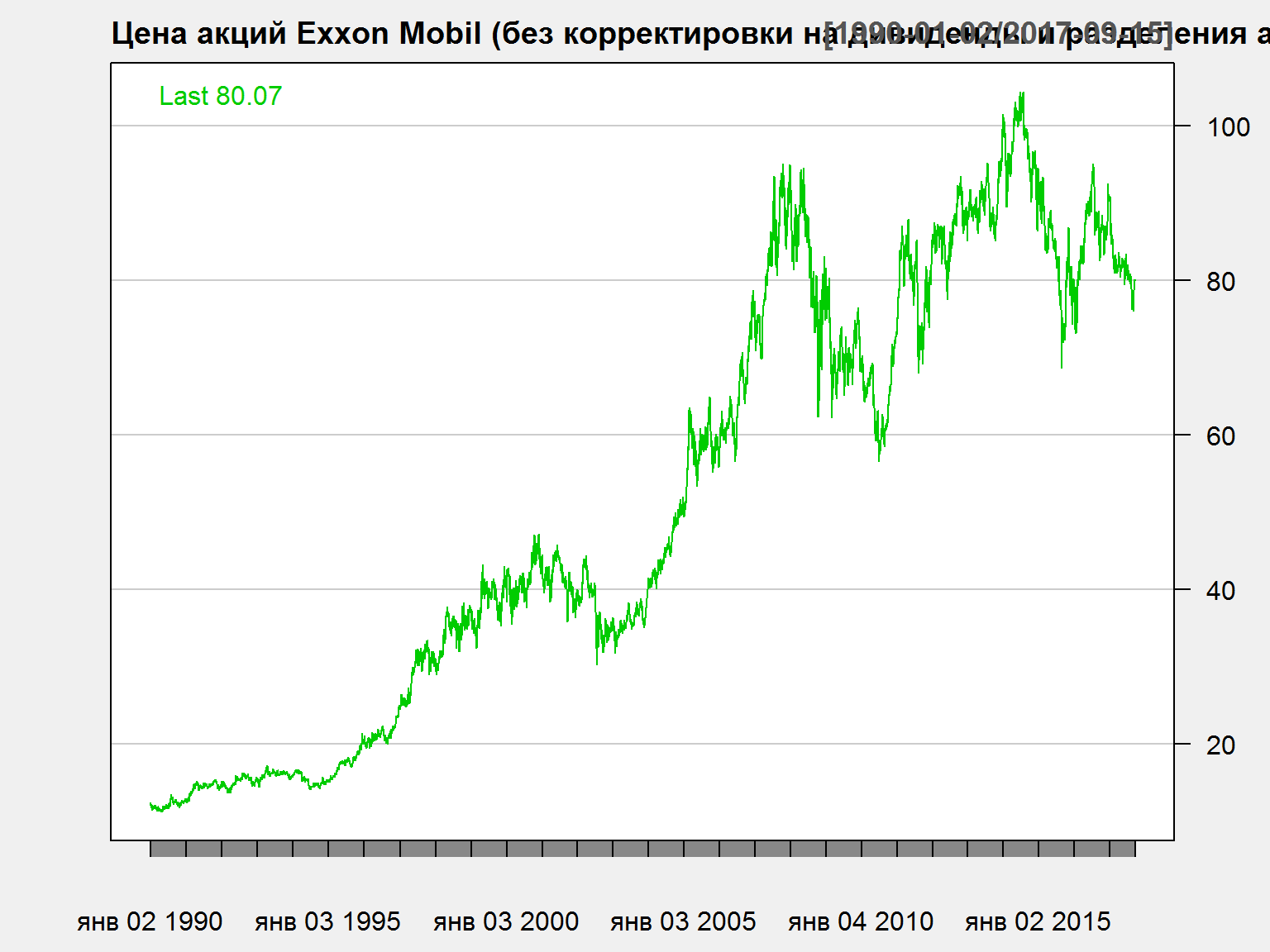
Акции Exxon Mobil - 2
chartSeries(XOM$XOM.Adjusted['1990::'], name = 'Цена акций Exxon Mobil (без корректировки на дивиденды и разделения акций)',multi.col = FALSE, theme = 'white')
Порядок корректировки цены акции на дивиденды
- Если дивиденды выплачиваются до периода времени \(t\), то валовая доходность в момент времени \(t\) определяется как
\[ 1+ R_t = \frac{P_t + D_t}{P_{t-1}} = \frac{P_t}{P_{t-1}} + \frac{D_t}{P_{t-1}} \]
Нетто-доходность будет \(r_t = log(1+R_t) = log(P_t + D_t) - log(P_{t-1})\).
- Для дневных доходностей, дивидендная доходность равна нулю во все дни, когда не выплачиваются дивиденды. Для компаний, которые не выплачивают дивиденды, полная доходность и ценовая доходность равны друг другу.
- Для скорректированной (adjusted) цены акции стоимость дивидендов вычитается из цены закрытия на дату “отсечки”. Дата “отсечки” – последняя дата, на которую признается право акционера на получение дивидендов.
- Предположим, что цена закрытия акций Роснефти составила 300 рублей в четверг. После закрытия торгов Роснефть объявила о том, что выплатит дивиденды в размере на 10 рублей на акцию. Тогда скорректированная цена акции составит 290 рублей = 300 - 10.
- Корректировка на дивиденды “меняет”" цены в прошлом. Текущая скорректированная цена и текущая цена на рынке должны быть равны другу другу. Поэтому корректируются именно исторические данные, а не текущие.
Полная доходность (total return) для акций Газпрома
- Для многих российских бумаг, разница между полной доходностью и ценовой доходностью также важна!
- В Bloomberg можно оценивать total return для российских бумаг
К сожалению, доступные бесплатные источники не предоставляют информацию по полной доходности для российских активов. Bloomberg предоставляет данные по дивидендам и total return для российских бумаг.
Сравнение доходностей нескольких бумаг за период времени
нарисуем график трех бумаг – Amazon, Google и Facebook. Акции Facbook торгуются с мая 2012 года (IPO). Поэтому график начинается с 18 мая 2012 года.
symbols = c('AMZN', 'GOOG', 'FB')
getSymbols(symbols,src="yahoo", from ='2012-05-18') # from yahoo finance
## [1] "AMZN" "GOOG" "FB"
tech_stocks = merge(AMZN$AMZN.Adjusted, GOOG$GOOG.Adjusted, FB$FB.Adjusted )
names(tech_stocks) = c('AMZN', 'GOOG', 'FB')
plot.xts(tech_stocks,legend.loc = 'top', main = 'Динамика цен на акций интернет-компаний')
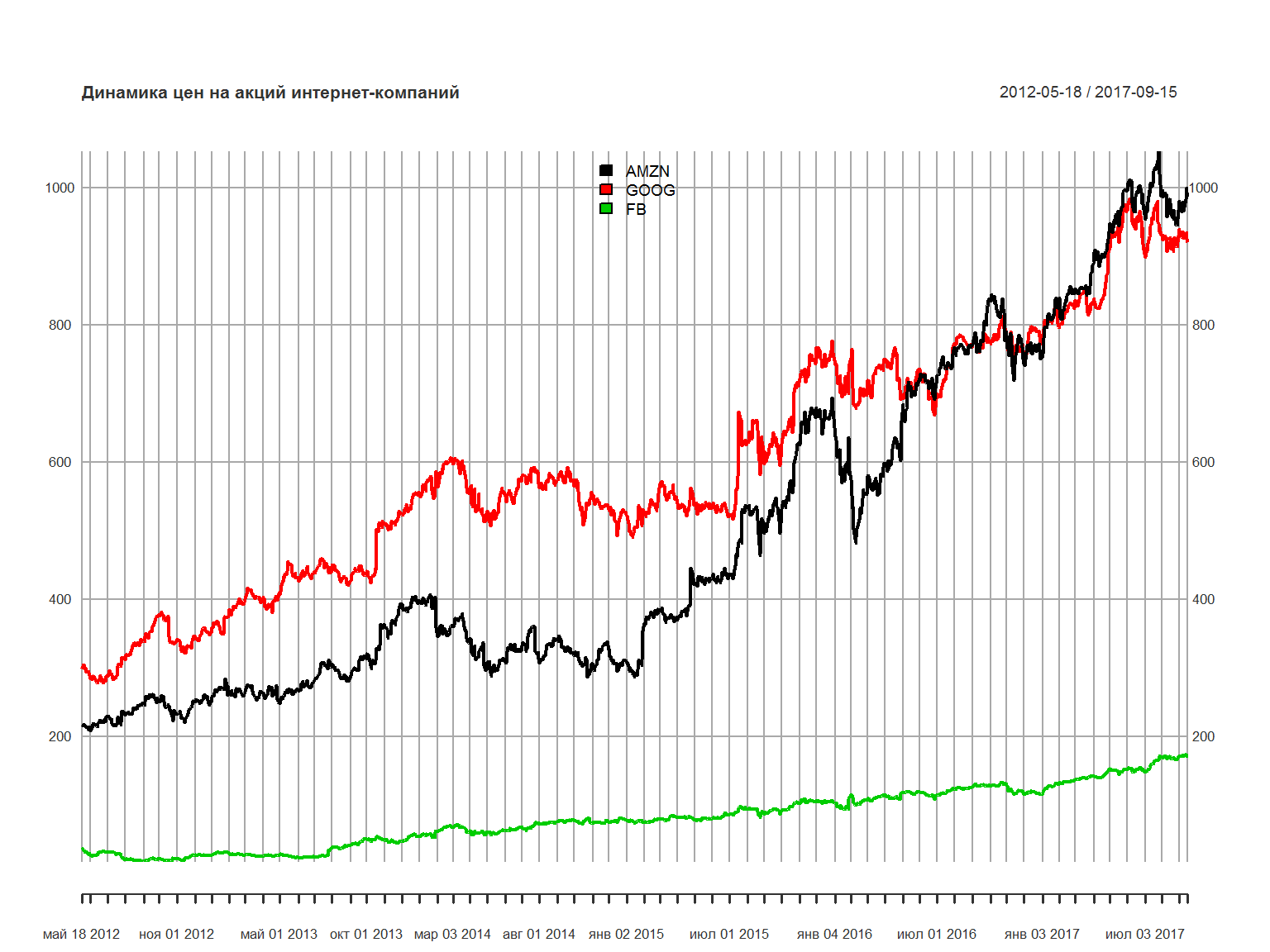
нормируем график по состоянию на 18 мая 2012 года – поделим значения каждой бумаги на соответствующее значение в этот день:
library(xts)
tech_stocks2 <- tech_stocks
tech_stocks2$AMZN <- tech_stocks2$AMZN / as.numeric(xts::first(tech_stocks2$AMZN))
tech_stocks2$GOOG <- tech_stocks2$GOOG / as.numeric(xts::first(tech_stocks2$GOOG))
tech_stocks2$FB <- tech_stocks2$FB / as.numeric(xts::first(tech_stocks2$FB))
plot.xts(tech_stocks2,legend.loc = 'top', main = 'Нормированная динамика цен на акций интернет-компаний')
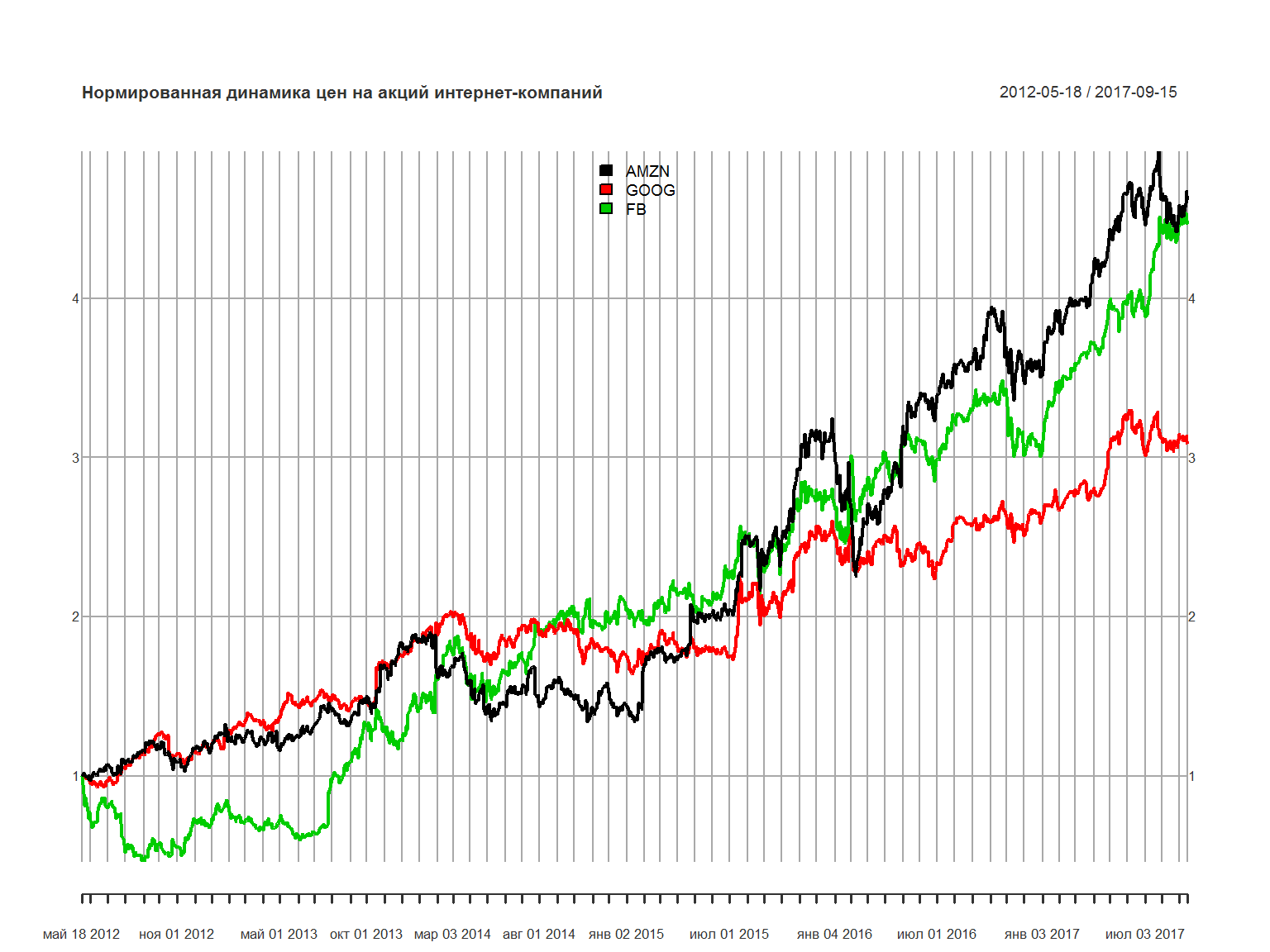
Позволяет ли доходность вчера предсказать доходность сегодня?
data$sp500.ret.lag <- c(NA, data$sp500.ret[-nrow(data)])
fancy.plot (data$sp500.ret.lag, data$sp500.ret, col=2, cex=0.5, xlab="Доходность вчера", ylab="Доходность сегодня", asp=1)
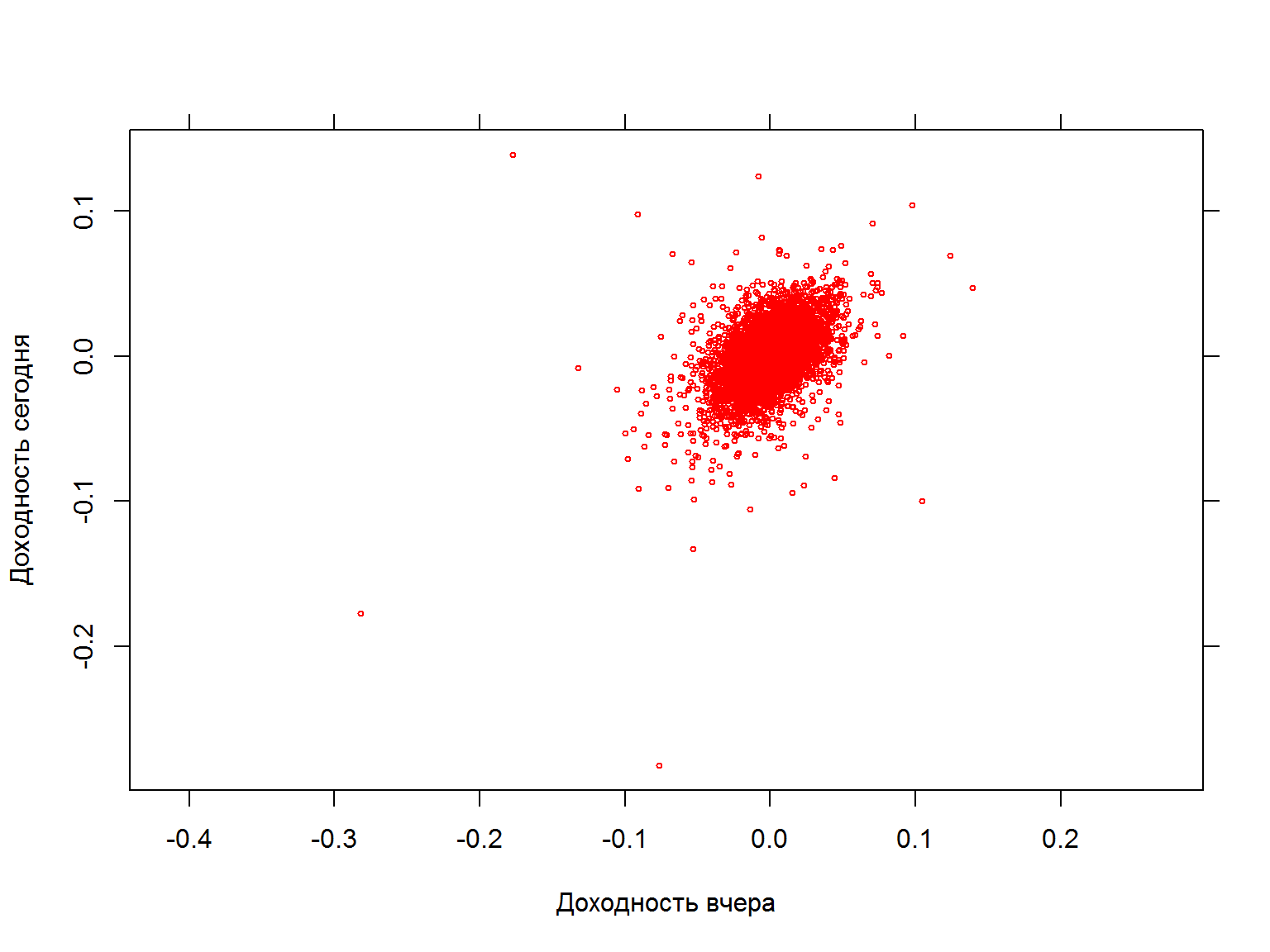
Позволяет ли доходность вчера предсказать доходность сегодня? (2)
посчитаем регрессию для доходностей
model.ret <- lm(data = data, sp500.ret ~ sp500.ret.lag)
summary(model.ret, digits = 4)
##
## Call:
## lm(formula = sp500.ret ~ sp500.ret.lag, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.244473 -0.005979 0.000006 0.006008 0.226014
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.970e-04 9.241e-05 3.214 0.00131 **
## sp500.ret.lag 4.929e-01 6.667e-03 73.939 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.01205 on 17032 degrees of freedom
## (3 observations deleted due to missingness)
## Multiple R-squared: 0.243, Adjusted R-squared: 0.2429
## F-statistic: 5467 on 1 and 17032 DF, p-value: < 2.2e-16
Гистограмма доходностей – похожа на нормальное распределение?
hist(data$sp500.ret, breaks=100, col=2, xlab="Доходность", main="")
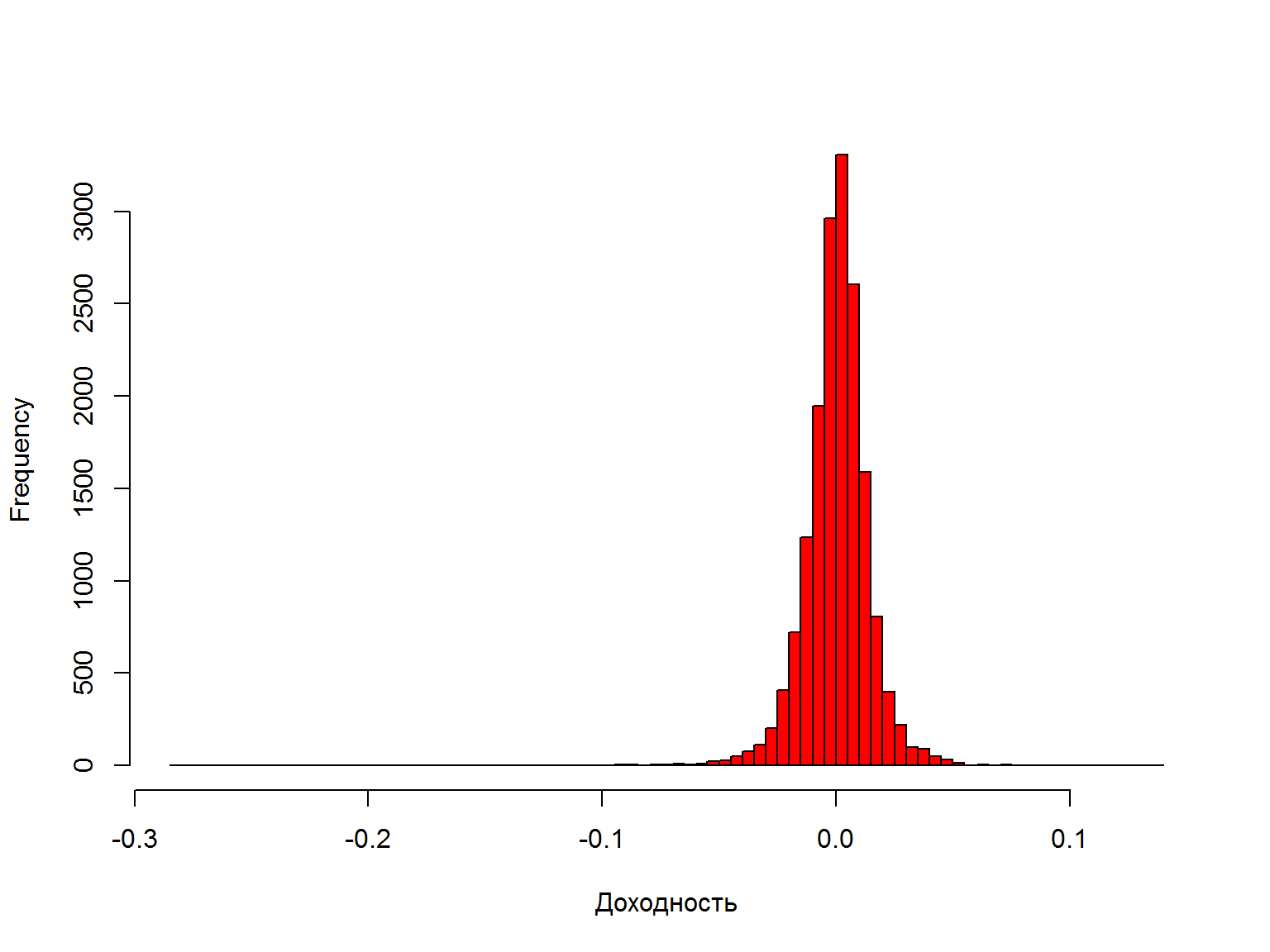
Доходности возвращаются к среднему значению (mean reversion)
library(ggplot2)
ggplot(tail(data,1000), aes(x=sp500.ret)) +
geom_histogram( aes(y=..density..),
colour="black",
fill="white") +
stat_function(fun=dnorm, args=list(mean=mean(data$sp500.ret, na.rm=TRUE), sd=sd(data$sp500.ret, na.rm=TRUE)), col = 'red')+theme_minimal()
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
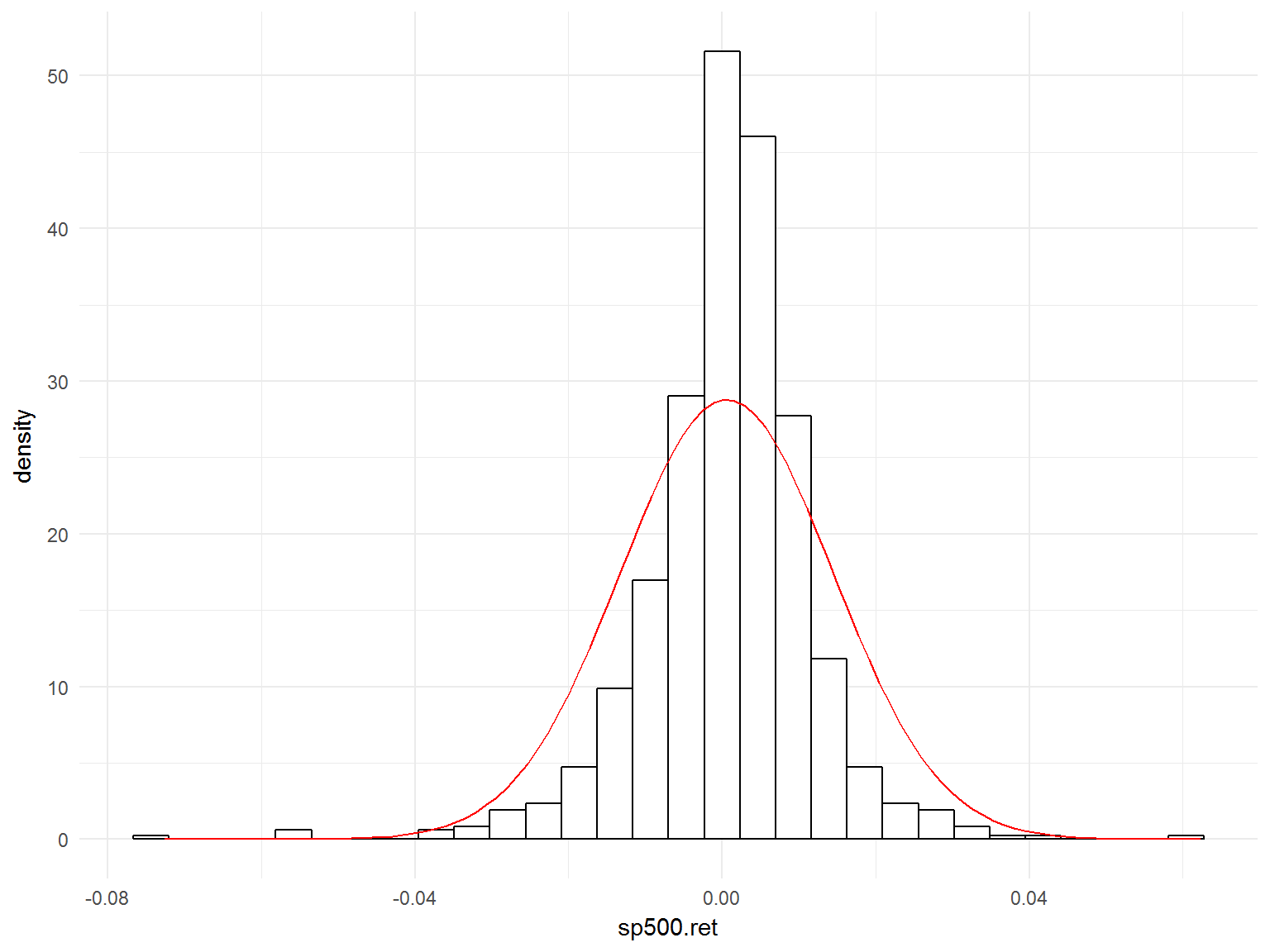
Эксцесс и нормальность доходностей
- Эксцесс (kurtosis) – мера “остроты” пика распределения случайной величины.
- Эксцесс нормально распределенный величины равен 3. Поэтому обычно в формуле эксцесса вычитают 3 для того, чтобы коэффициент эксцесса нормального распределения был равен нулю. Он положителен, если пик распределения около математического ожидания острый, и отрицателен, если пик очень гладкий.
## Loading required package: nortest
##
## Attaching package: 'nortest'
## The following object is masked _by_ '.GlobalEnv':
##
## ad.test
kurtosis(data$sp500.ret, na.rm=TRUE) # избыточный эксцесс(excess kurtosis), 0 -- для нормального распределения
## [1] 17.04439
nortest::ad.test(data$sp500.ret)
##
## Anderson-Darling normality test
##
## data: data$sp500.ret
## A = 163.79, p-value < 2.2e-16
qqnorm(data$sp500.ret) # график кванталь-квантиль
qqline(data$sp500.ret)
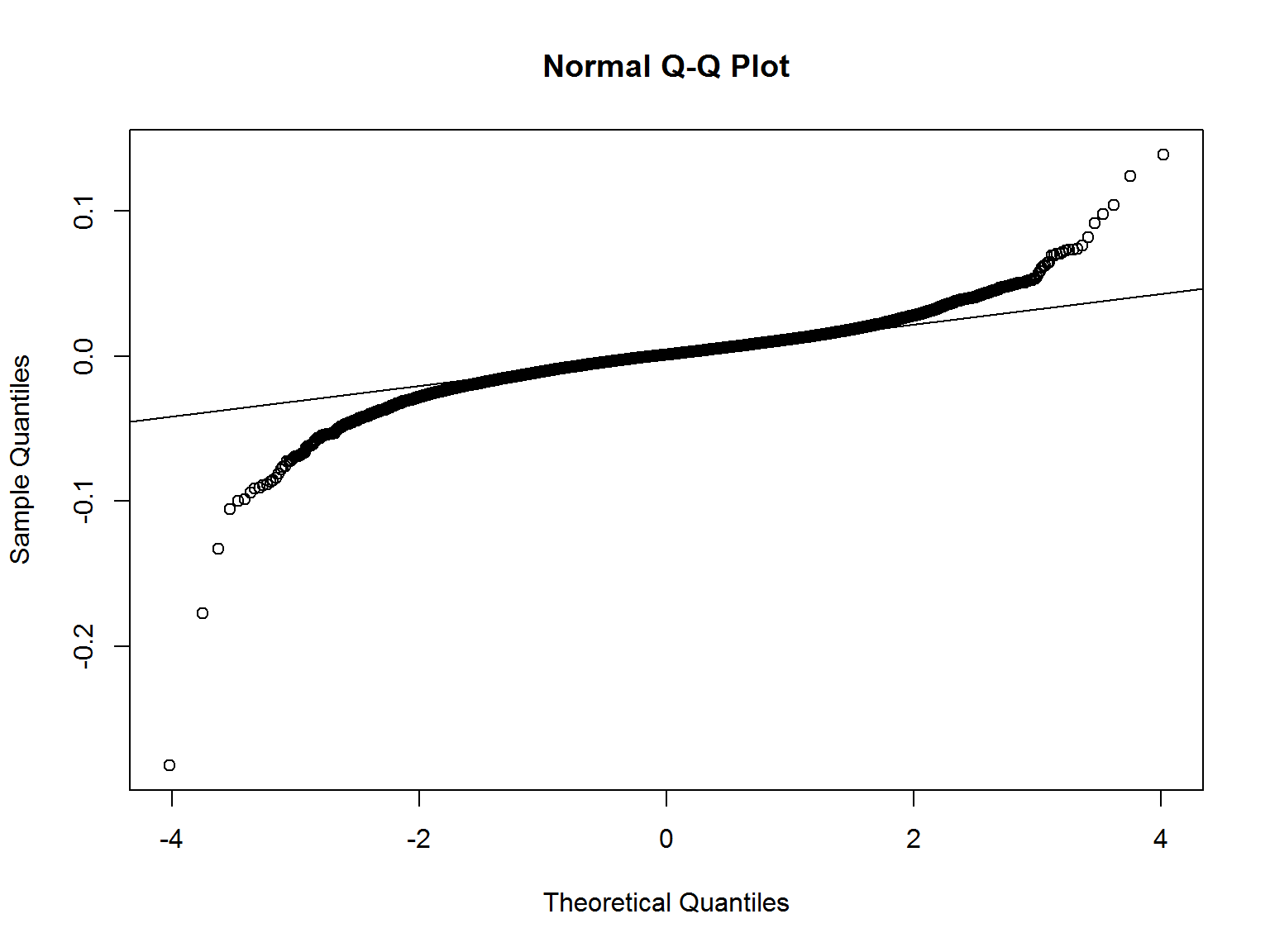
Доходности имеют избыточный эксцесс (“тяжелые хвосты” – heavy tails).
Волатильности устойчивы (persistent) во времени
квадраты доходностей
fancy.plot(data$date, (data$sp500.ret)^2, t="l", xlab="Date", ylab="Квадрат доходности", col=2)
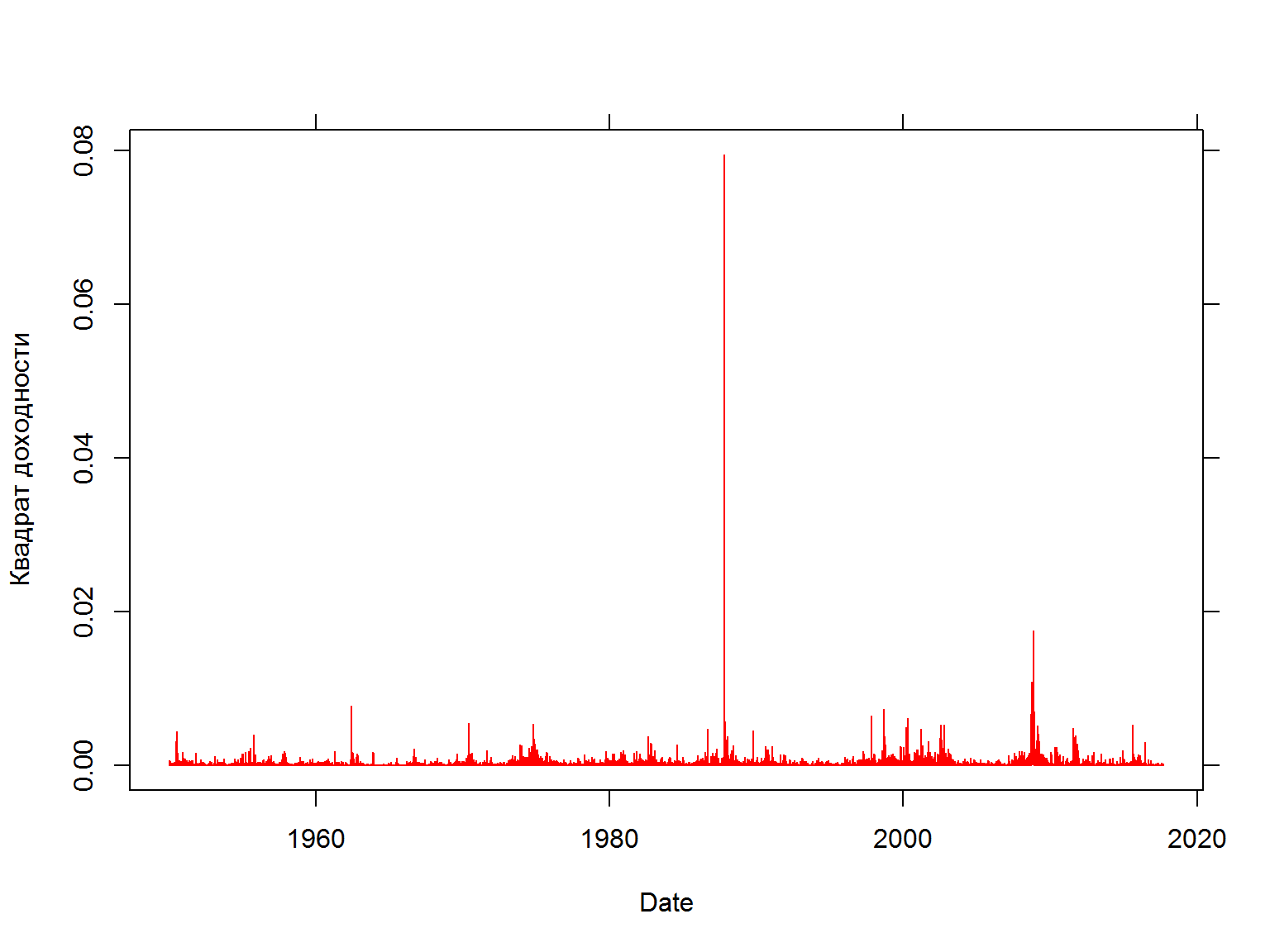
mod.vol <- lm(data =data, sp500.ret^2 ~ sp500.ret.lag^2)
cor(data$sp500.ret,data$sp500.ret.lag, use = "complete.obs" )
## [1] 0.4929397
cor(data$sp500.ret^2,data$sp500.ret.lag^2, use = "complete.obs" )
## [1] 0.4495745
fancy.plot(data$date, abs(data$sp500.ret), t="l", xlab="Date", ylab="Абсолютное значение доходности", col=2)
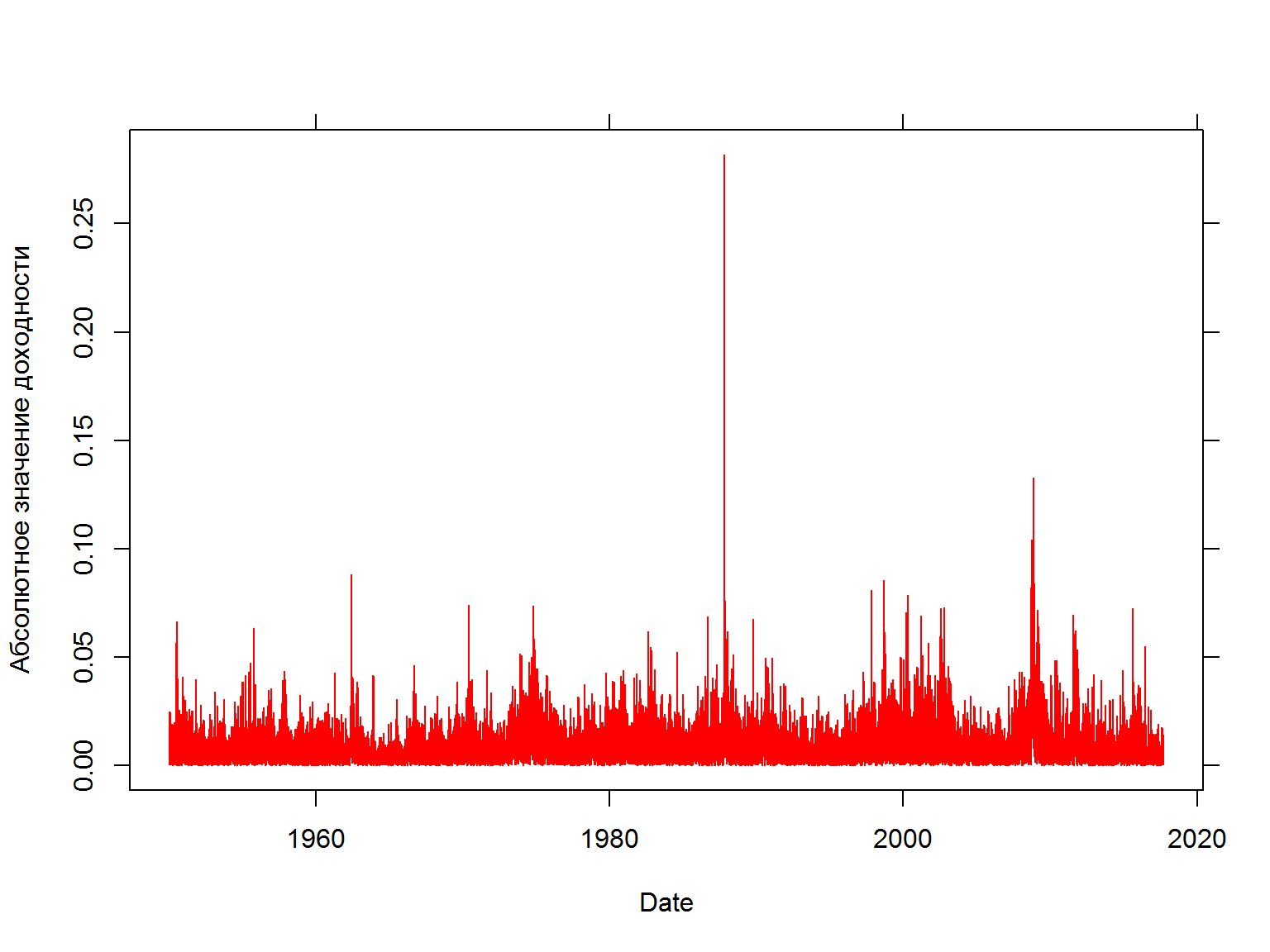
Основные особенности финансовых серий:
- Многие финансовые серии растут экспоненциально и имеют изменяющуюся волатильность в зависимости от уровня значений.
- Наблюдения, которые находятся рядом, скоррелированны между собой.
- Доходности имеют избыточный эксцесс (heavy tails) и не распределены нормально.
- Волатильность устойчива во времени (persistent) и часто в финансовых данных наблюдаются кластеры волатильности - периоды большой и низкий волатильности сохраняются определенное время.
Понятие стационарности и почему оно важно
- Стандартным допущением при анализе временных рядов является стационарность.
- Серия является стационарной, если параметры генерирующего процесса не меняются со временем
- Рассмотрим две серии А и B. Параметры серии А (среднее арифметическое, стандартное отклонение) - не меняются со временем
mu = 0
sigma = 1
T = 100
A <- rnorm(T, mu, sigma)
plot(A, type = 'l')
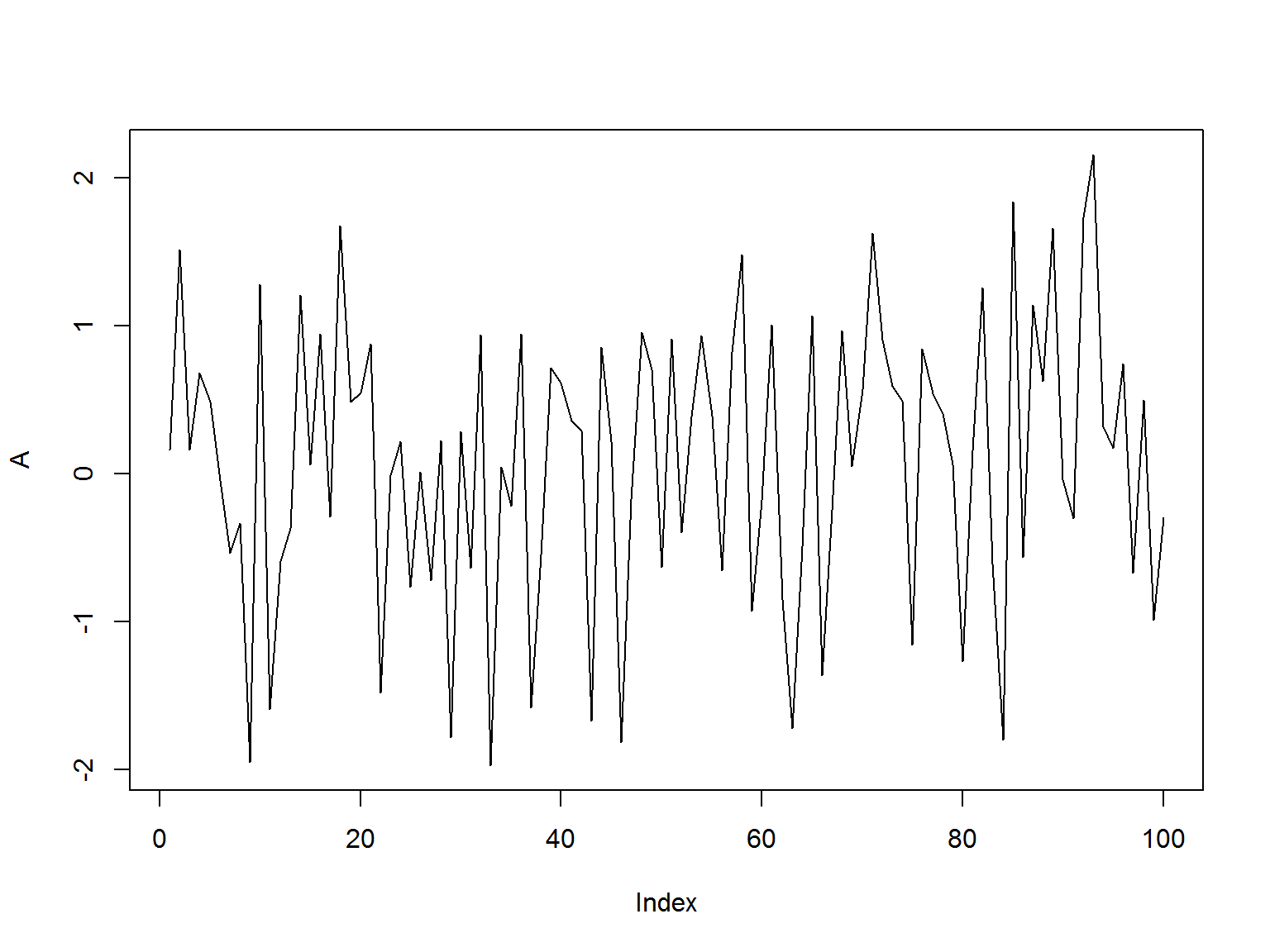
Понятие стационарности и почему оно важно (2)
Для серии B среднее (mean) меняется со временем
mu = 0
sigma = 1
T = 100
B <- rep(0, 100)
t <- seq(0,T, by = 1)
for(i in 1:T){
B[i] <- rnorm(1, 0.05*i, sigma)
}
plot(B, type = 'l')
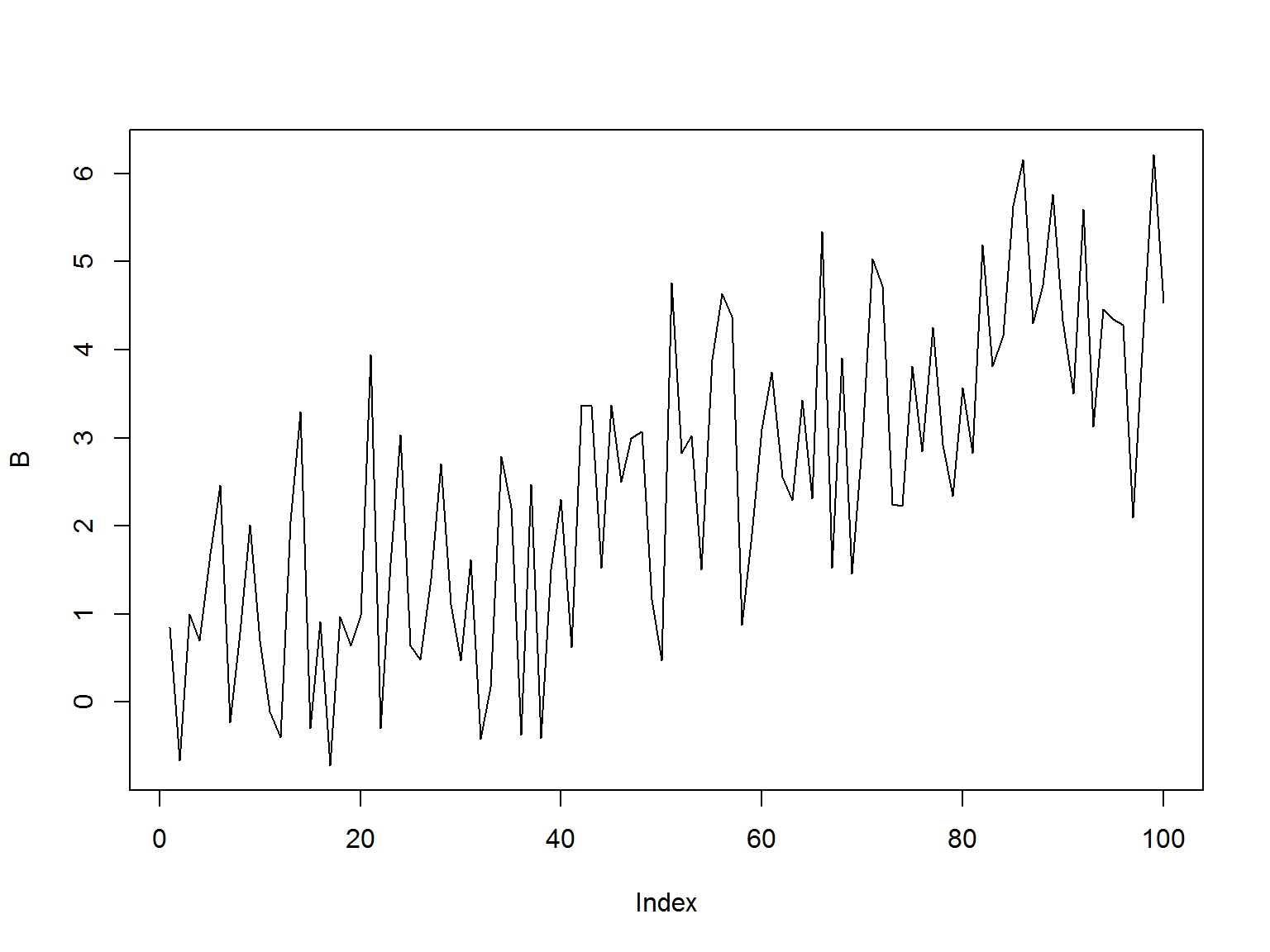
Почему не-стационарнасть опасна?
- Многие статистические цены требуют, чтобы данные, которые тестируются, были стационарны.
К примеру, возьмем среднее для не-стационарного ряда (серия B, сгенерированная ранее):
plot(B, type = 'l')
abline(h = mean(B), col = 'red')
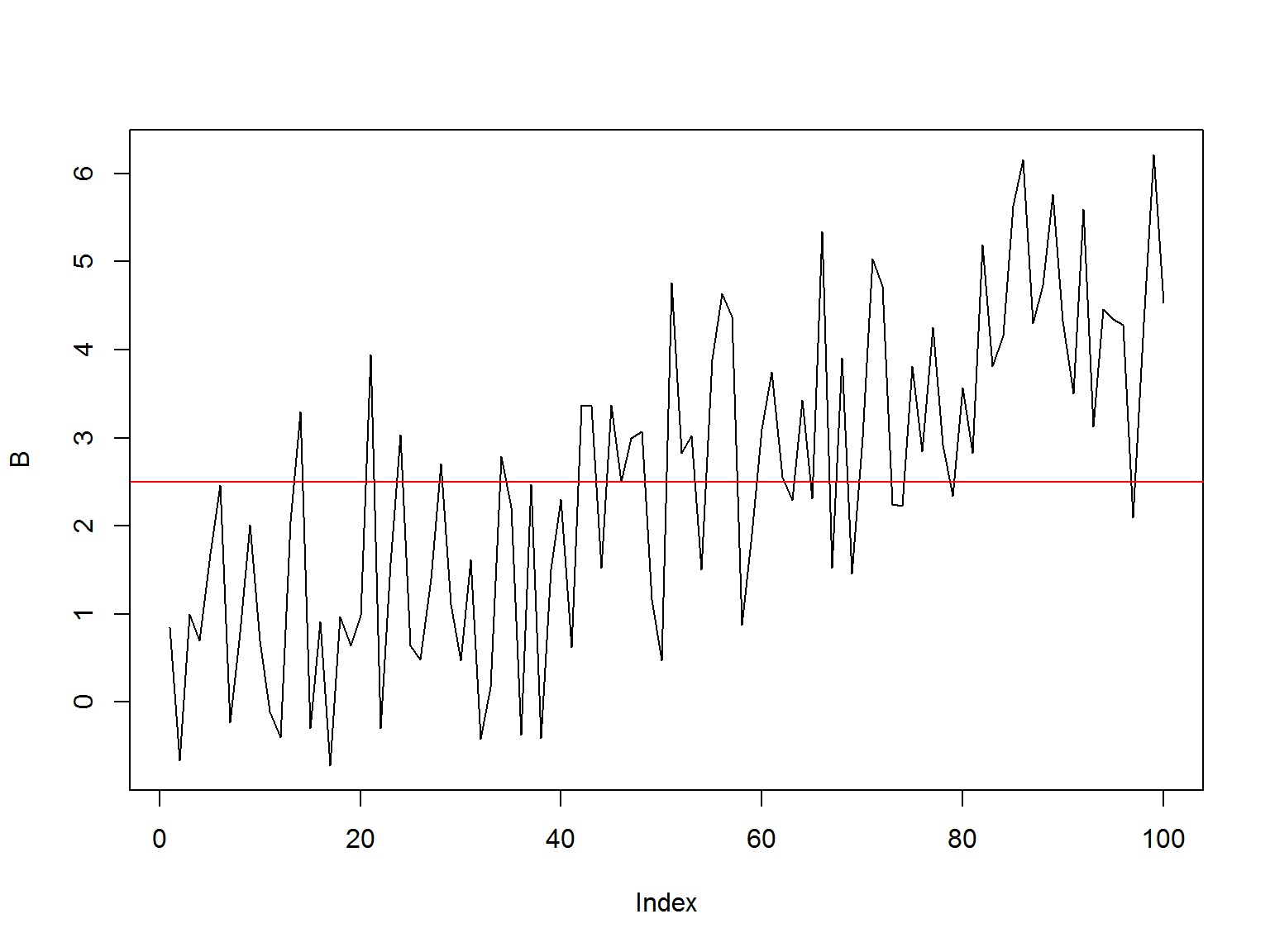
- Рассчитанное среднее значение для всех точек бессмысленно с точки зрения прогнозирования будущих значений.
- Устойчивость параметров во времени дает основания считать, что рассчитанные по прошлым данным параметры, будут иметь значение и в будущем.
Проверим стационарность с помощью стандартного теста
library(tseries)
adf.test(A)
##
## Augmented Dickey-Fuller Test
##
## data: A
## Dickey-Fuller = -4.0116, Lag order = 4, p-value = 0.01148
## alternative hypothesis: stationary
##
## Augmented Dickey-Fuller Test
##
## data: B
## Dickey-Fuller = -3.8536, Lag order = 4, p-value = 0.0191
## alternative hypothesis: stationary
Тесты иногда ошибаются!
Использованные источники:
- “An Introduction to Analysis of Financial Data with R” (Ruey S. Tsay)
- “Statistics and Data Analysis for Financial Engineering” (David Ruppert & David Matteson)
- Analyzing Financial Data and Implementing Financial Models Using R (Clifford Ang)
- Forecasting Financial Time Series (Patrick Perry)