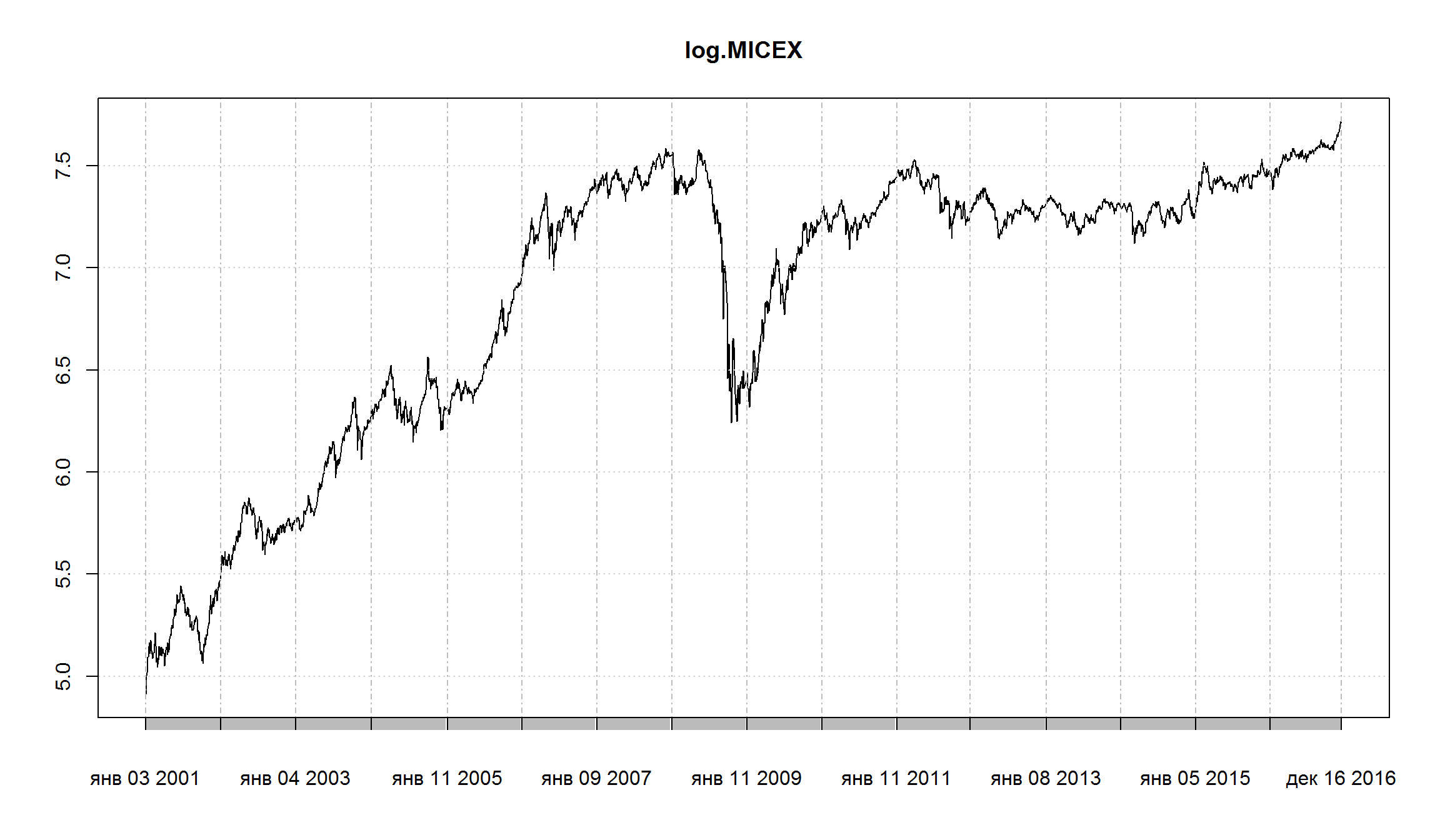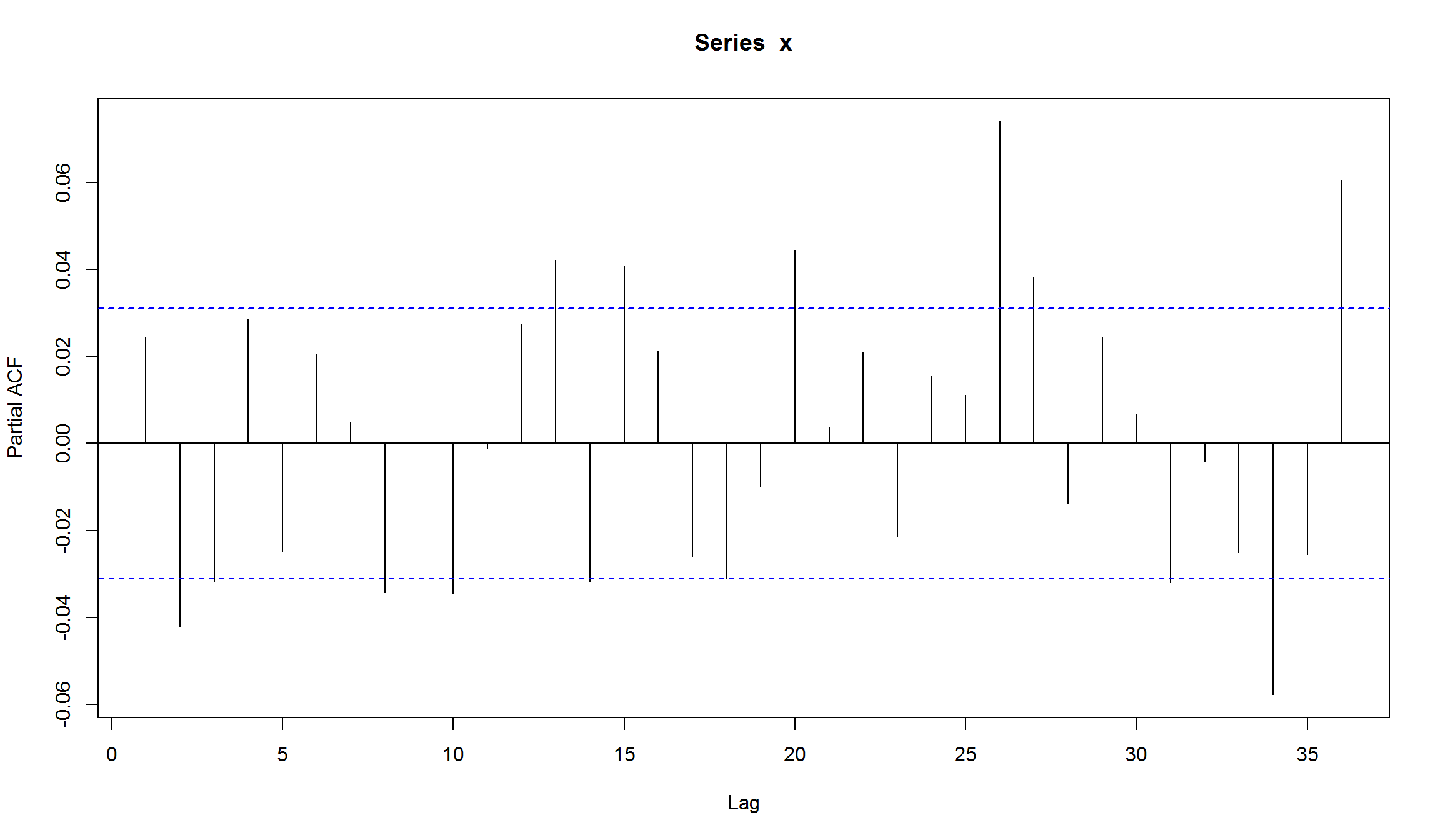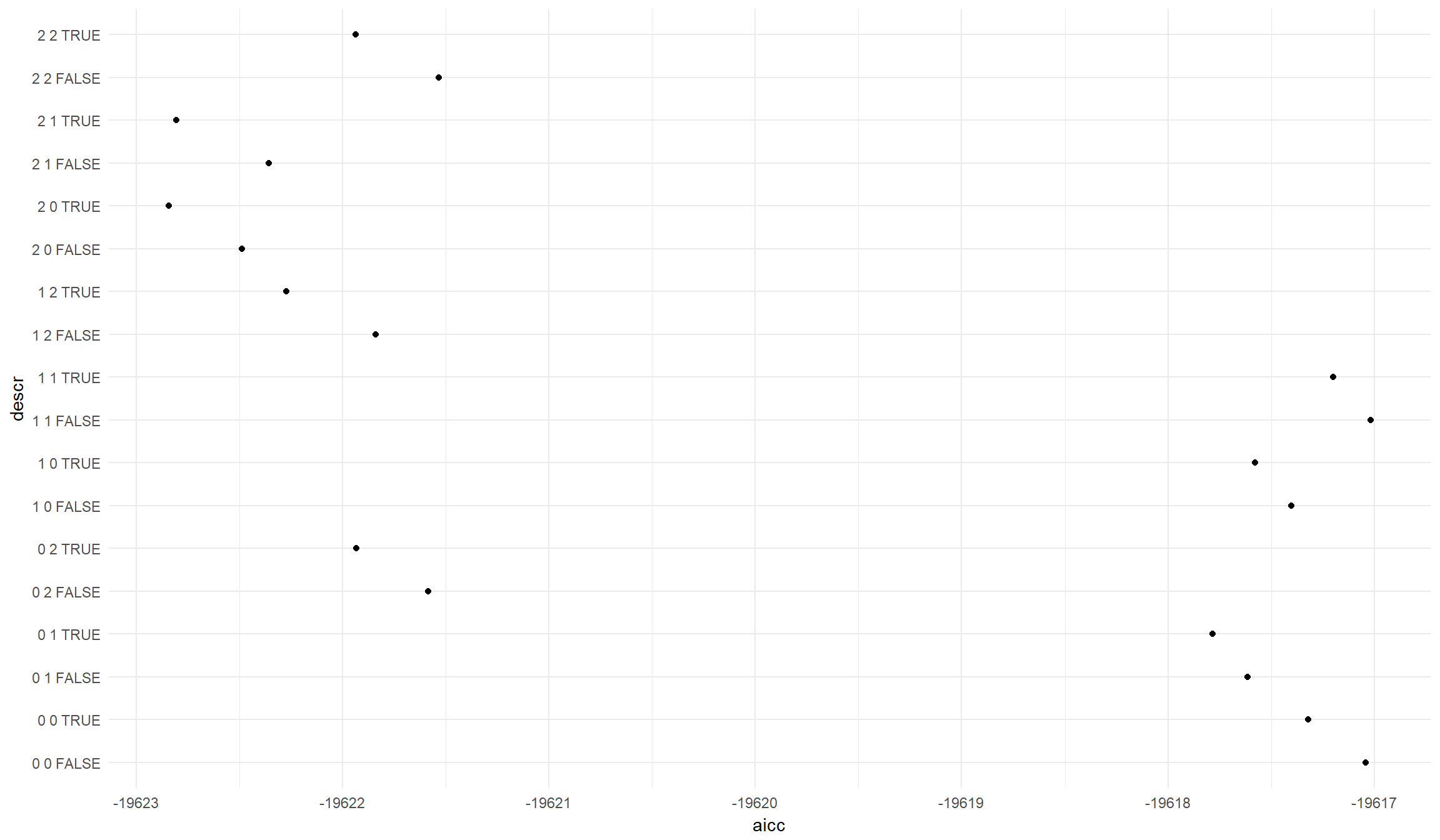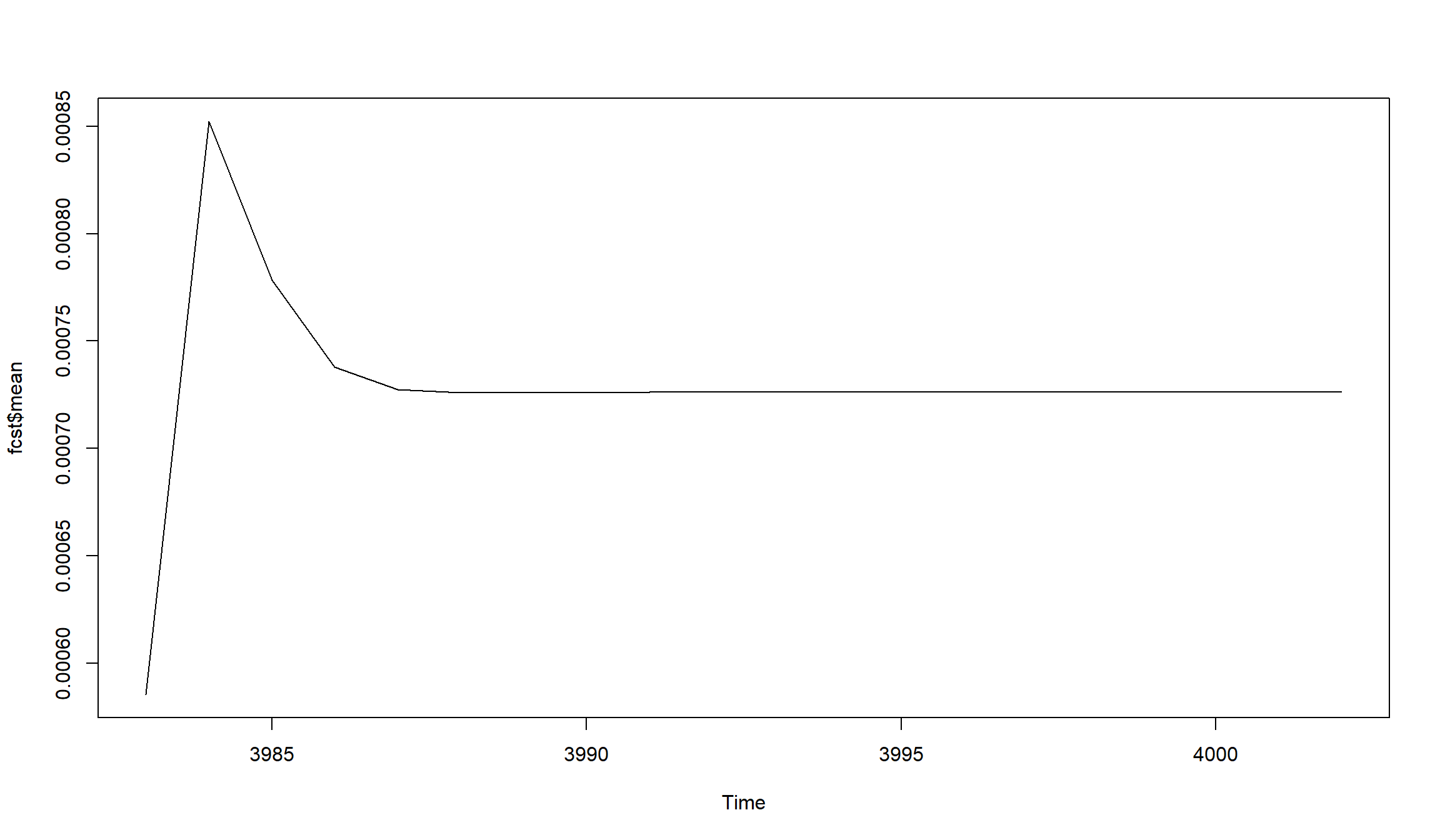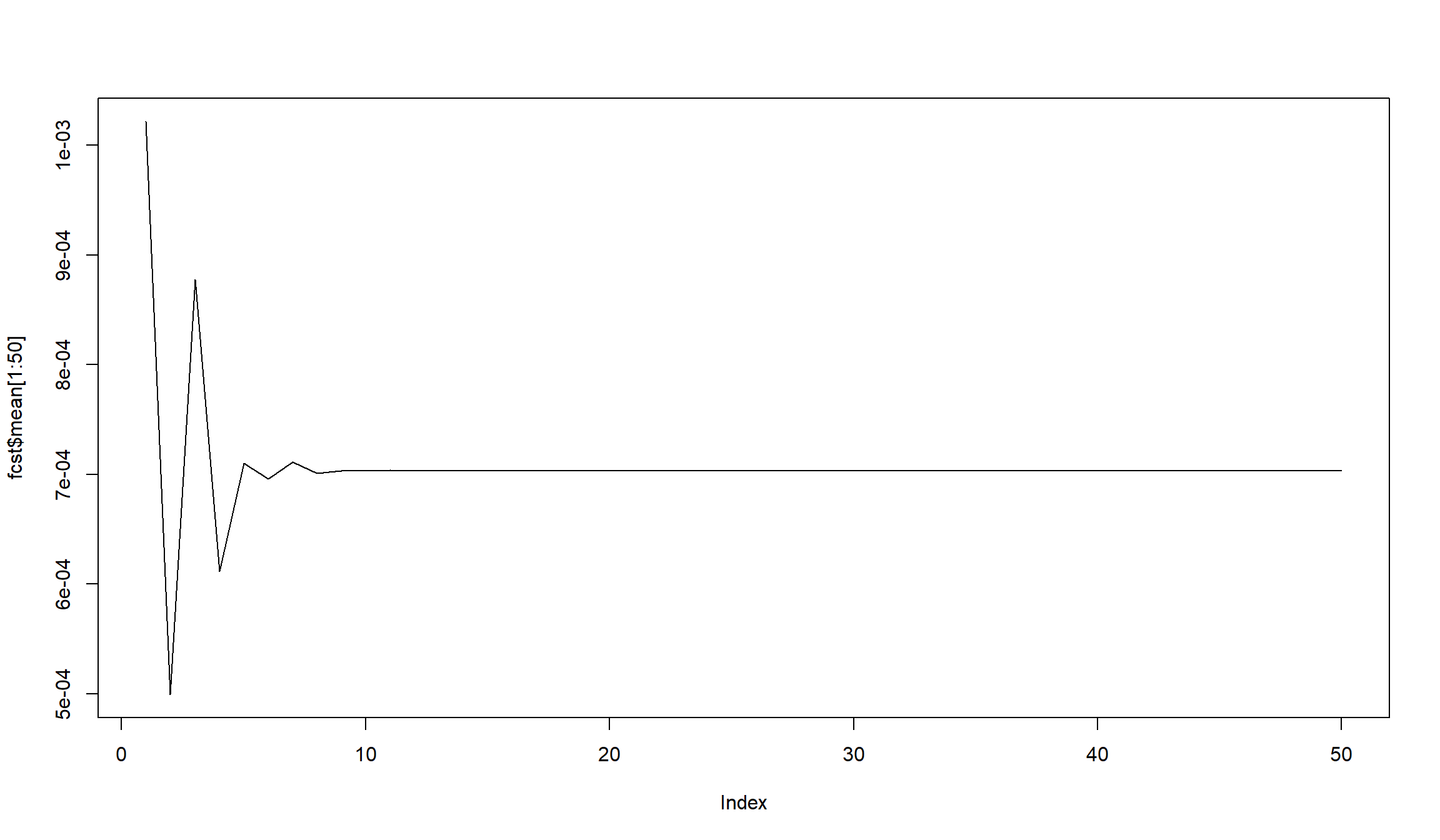Цели лекции

• понять основные принципы moving average (MA) моделей
• научиться симулировать MA-модели
• научиться оценивать MA-модели на финансовых данных в R
• понять принципы применения критериев AIC и BIC для выбора подходящей модели
• понять, как строятся ARMA модели
  
• научиться строить прогнозы для ARMA моделей

Moving average

• На прошлой лекции мы рассмотрели авторегрессионные (AR) модели. В конечном счете мы пришли к тому, что AR-модели для настоящих финансовых данных требуют слишком большого количества параметров для оценки и приводят к “подгонке” (overfitting).
• MA-модели схожи с AR-моделями, однако в отличие от них модель представляет собой не линейную комбинацию прошлых значений, а линейную комбинацию прошлых компонент белого шума.
• МA-модель “видит” случайные шоки белого шума непосредственно для каждого текущего значения серии. AR-модель же “видит” шоки косвенным образом, через регрессирование к своим предыдущим значениям.
• Однако MA-модель порядка \(q\) “видит”" последние q шоков, в то время как AR(p) модель будет учитывать все предыдущие шоки с последовательным убыванием.

Определение MA-модели

Если серия временного ряда \({x_t}\) является моделью скользящего среднего порядка \(q\) (MA(q)), то это означает, что

\[ x_t = w_t + \beta_1 w_{t-1} + \ldots + \beta_q w_{t-q} \] где \({w_t}\) – это белый шум с \(E(w_t)=0\) и дисперсией \(\sigma^2\).

• MA-модель всегда стационарна
• В MA-модель можно включать константу
• Обычно модели MA оценивают методом максимального правдоподобия (или другими численными методами). Аналитическая оценка затруднена.

MA(1) модель

Попробуем симулировать MA(1) c параметром \(\beta = 0.6\). То есть мы симулируем модель вида:

\[ x_t = w_t + 0.6 w_{t-1} \]

 set.seed(123)
 x <- w <- rnorm(100)
for (t in 2:100) x[t] <- w[t] + 0.6*w[t-1]
layout(1:2)
plot(x, type="l")
acf(x)

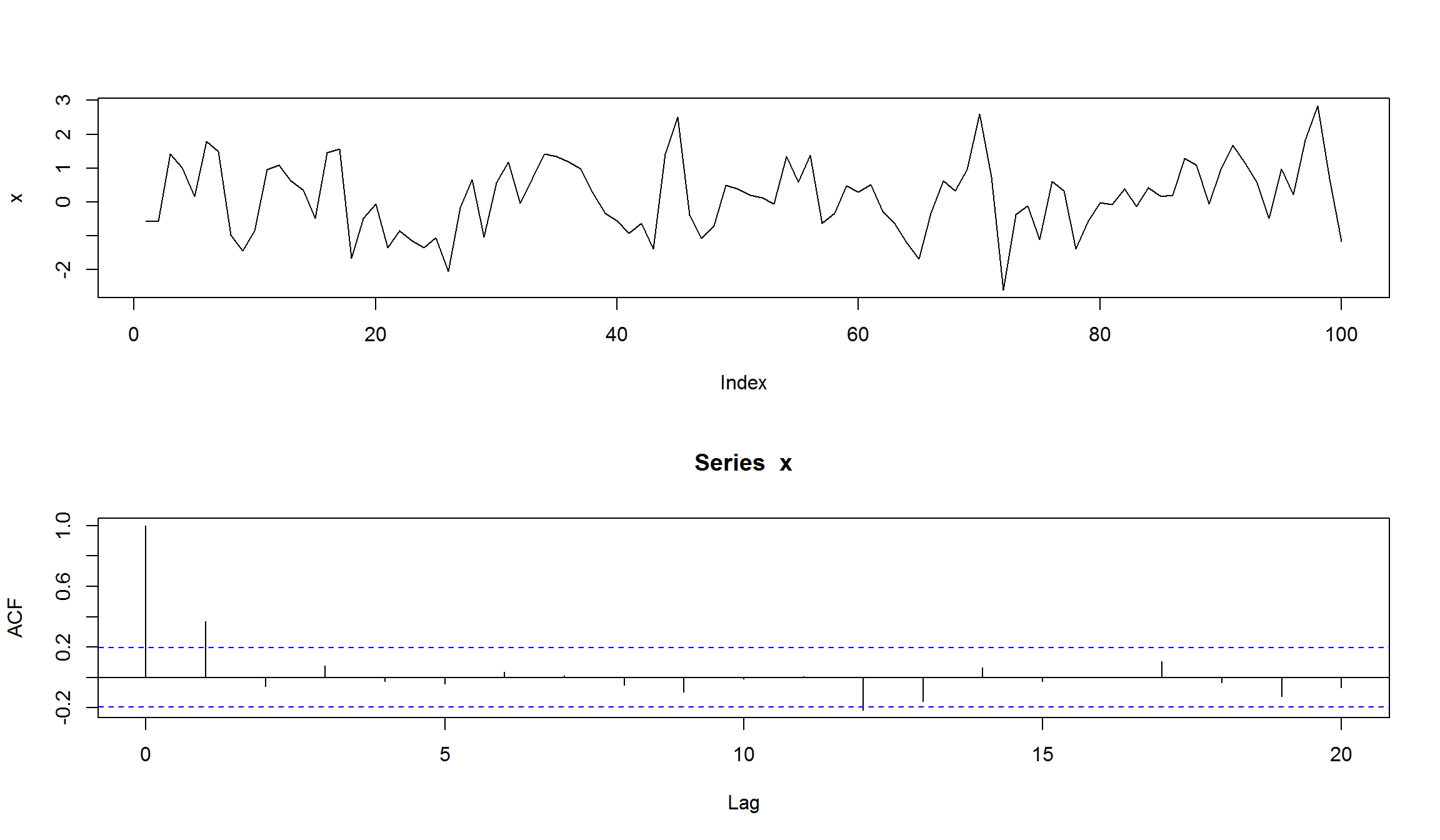
• Для MA-модели все автокорреляции с лагом \(k>q\) должны быть равны 0.

Оценка симулированной MA(1)-модели

Мы будем использовать функцию arima для оценки MA-моделей.

x.ma <- Arima(x, order=c(0, 0, 1))
x.ma

Series: x 
ARIMA(0,0,1) with non-zero mean 

Coefficients:
         ma1  intercept
      0.7240     0.1430
s.e.  0.0898     0.1546

sigma^2 estimated as 0.8271:  log likelihood=-131.76
AIC=269.53   AICc=269.78   BIC=277.34

x.ma$coef[1]+c(-1.96, 1.96)*0.0898  #доверительный интерваля для беты

[1] 0.5480362 0.9000522

confint(x.ma)

               2.5 %    97.5 %
ma1        0.5481109 0.8999776
intercept -0.1600075 0.4459076

• Коэффициенты отличаются значимым образом от 0.
• Доверительные интервалы включат “настоящие” значения коэффициентов

МA(1)-модель с коэффициентом -0.6

set.seed(123)
x <- w <- rnorm(100)
for (t in 2:100) x[t] <- w[t] - 0.6*w[t-1]
layout(1:2)
plot(x, type="l")
acf(x)

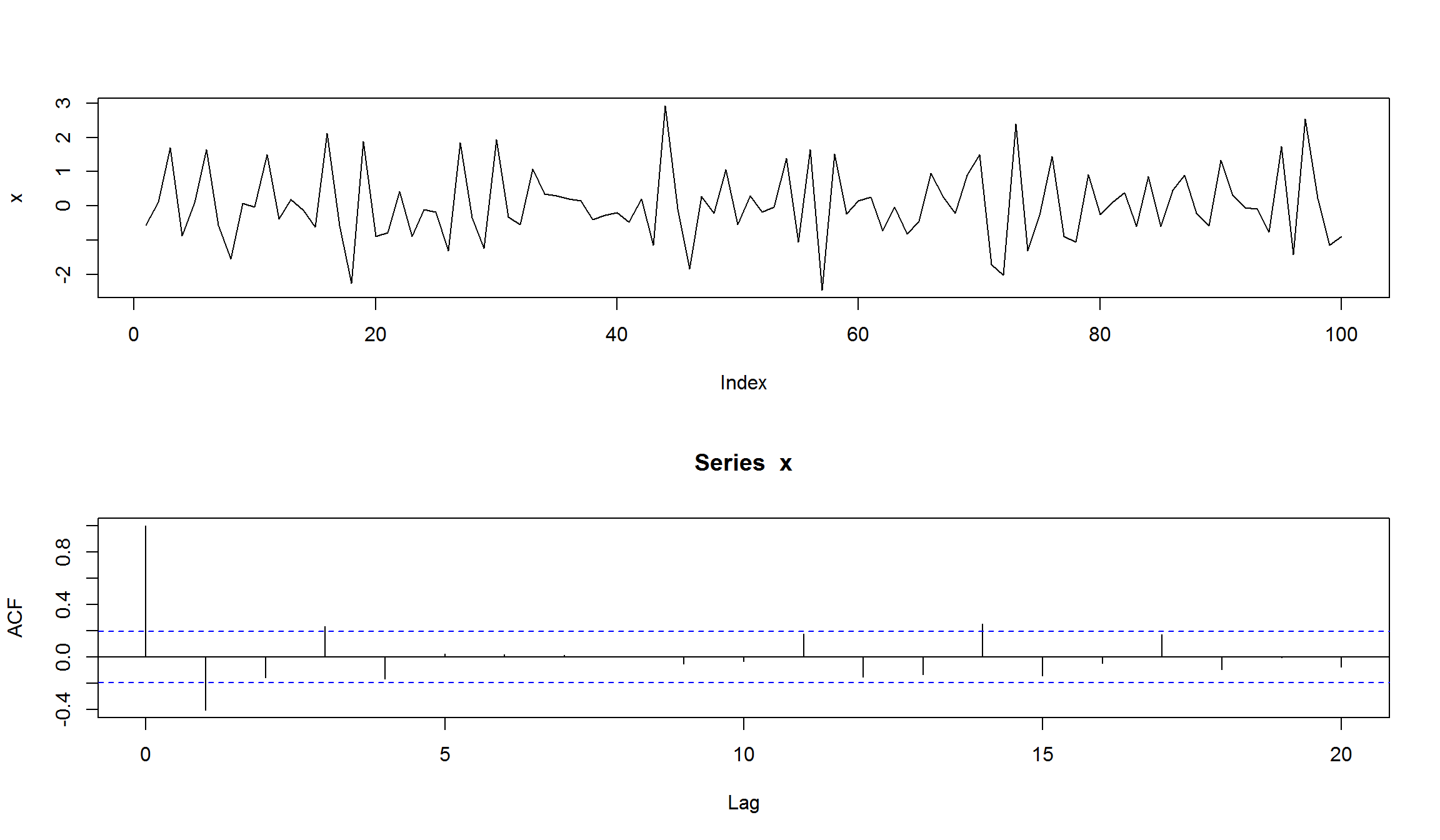
оценка модели

x.ma <- arima(x, order=c(0, 0, 1))
x.ma

Call:
arima(x = x, order = c(0, 0, 1))

Coefficients:
          ma1  intercept
      -0.6337     0.0370
s.e.   0.0788     0.0338

sigma^2 estimated as 0.8227:  log likelihood = -132.39,  aic = 270.78

x.ma$coef[1]+c(-1.96, 1.96)* 0.0788  #доверительный интерваля для беты

[1] -0.7881117 -0.4792157

MA(2)-модель

симулируем модель:

set.seed(123)
x <- w <- rnorm(1000)
for (t in 4:1000) x[t] <- w[t] + 0.6*w[t-1] + 0.3*w[t-2] 
layout(1:2)
plot(x, type="l")
acf(x)

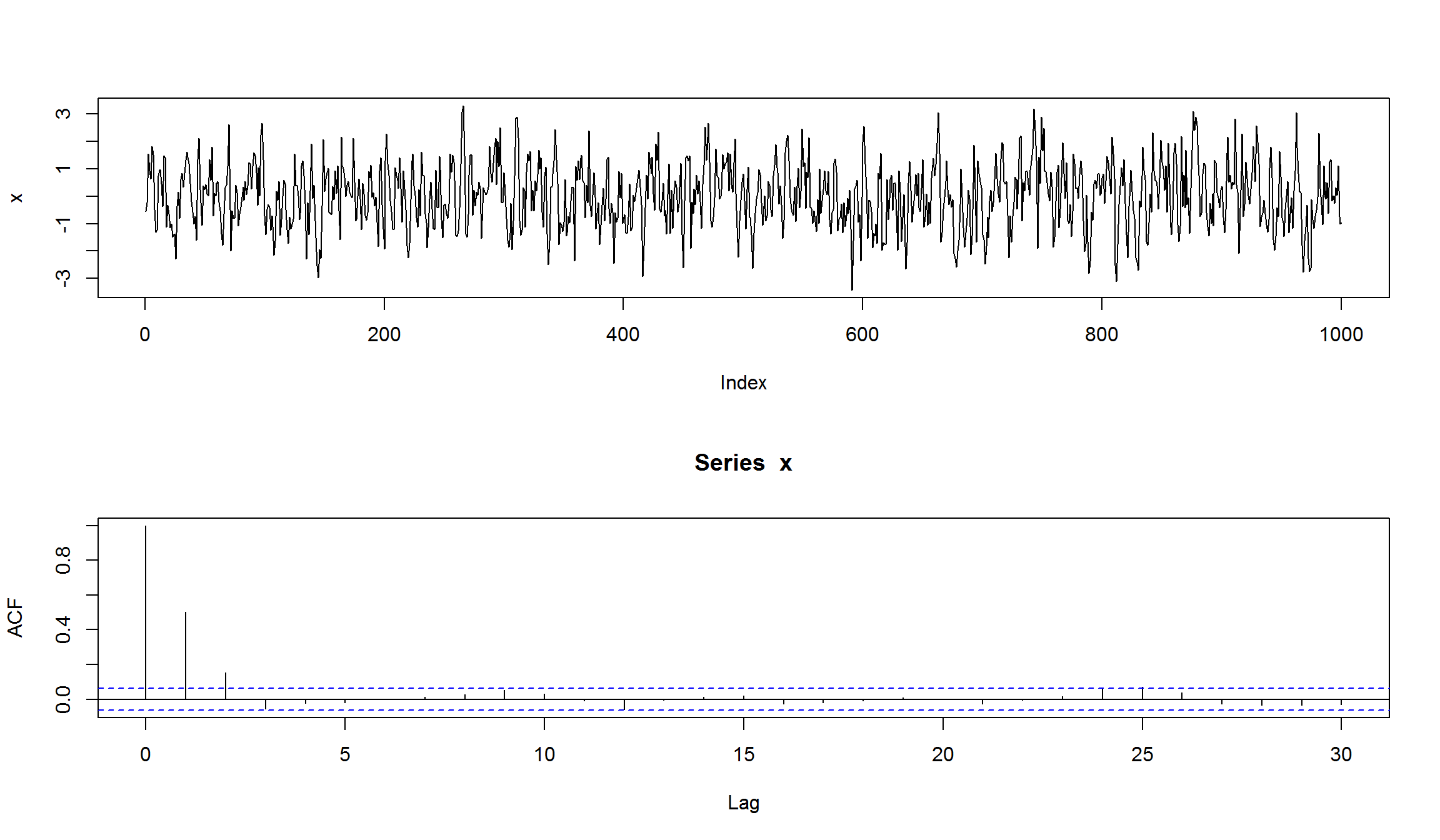
оценим модель

x.ma <- arima(x, order=c(0, 0, 2))
x.ma

Call:
arima(x = x, order = c(0, 0, 2))

Coefficients:
         ma1     ma2  intercept
      0.5852  0.2827     0.0307
s.e.  0.0311  0.0307     0.0585

sigma^2 estimated as 0.9822:  log likelihood = -1410.14,  aic = 2828.29

confint(x.ma)

                2.5 %    97.5 %
ma1        0.52422837 0.6461799
ma2        0.22251632 0.3429303
intercept -0.08393561 0.1453965

ACF для MA(1) и MA(2)

ma1 <- arima.sim(n=1000, model=list(ma=c(0.5)))
ma2 <- arima.sim(n=1000, model=list(ma=c(0.5, -0.3)))
par(mfrow=c(1,2))
Acf(ma1, na.action = na.omit)
Acf(ma2, na.action = na.omit)

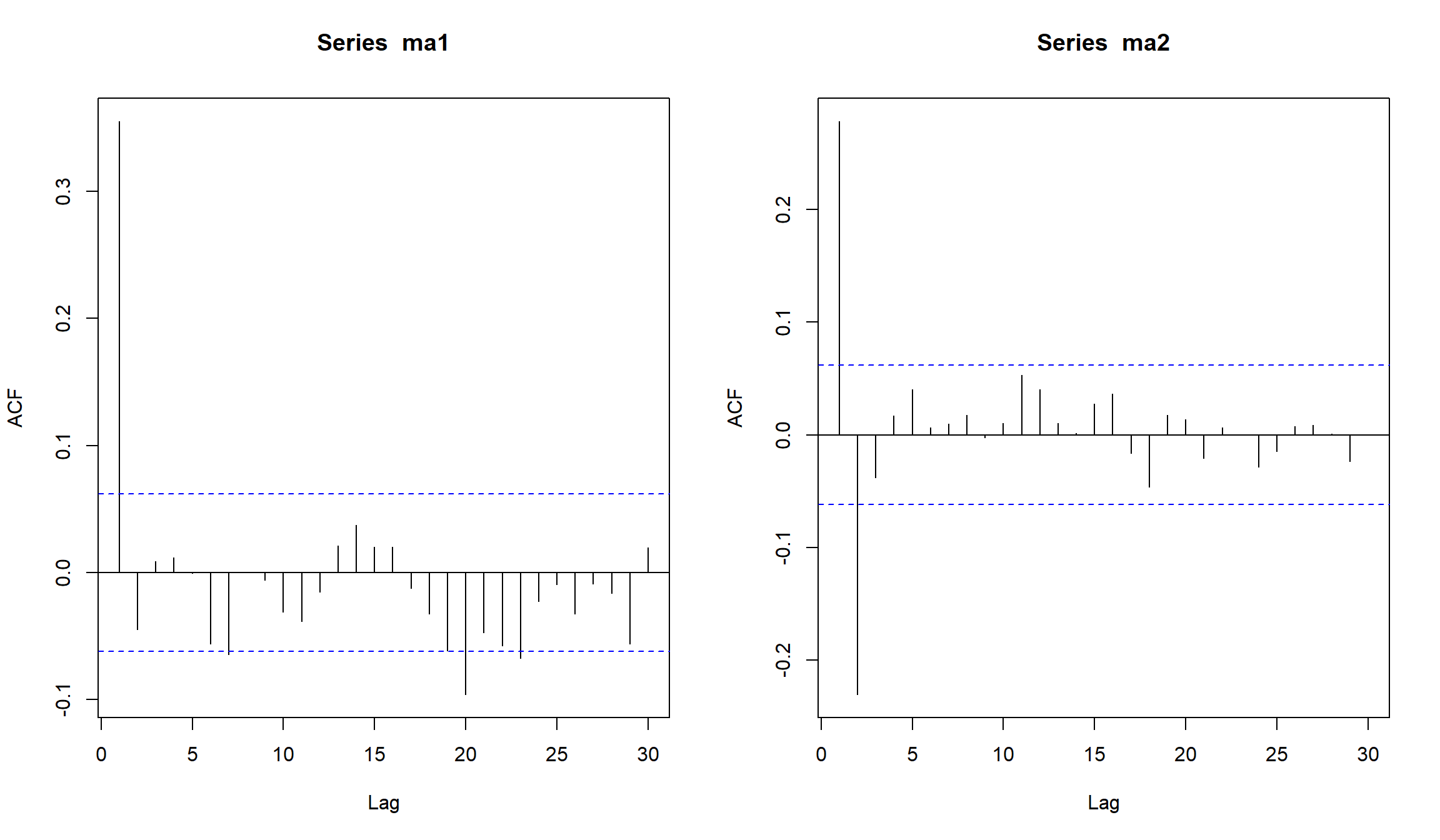
PACF для MA(1) и MA(2)

par(mfrow=c(1,2))
Pacf(ma1)
Pacf(ma2)

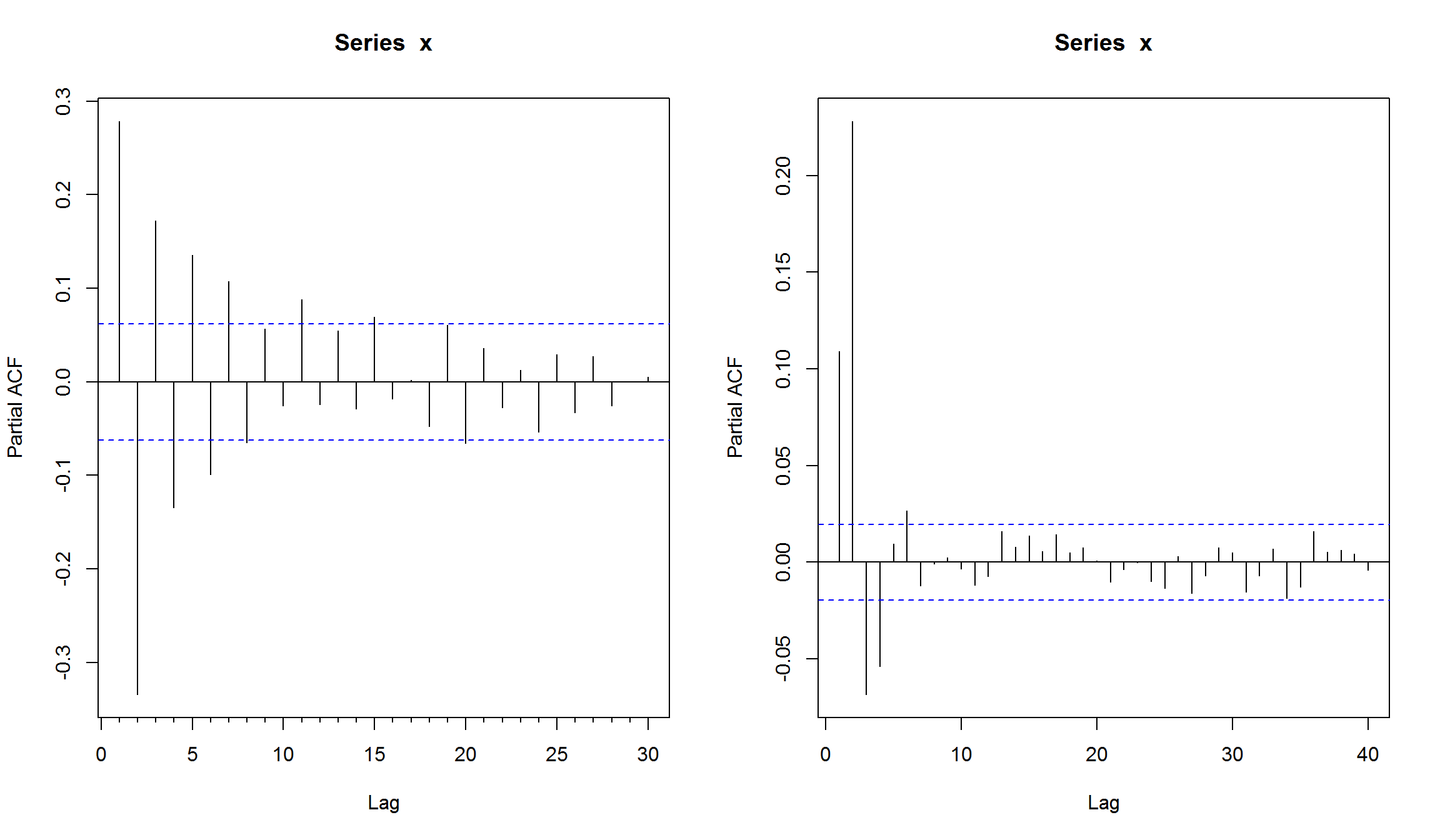
Индекс ММВБ

#library(rusquant)
#MICEX <- rusquant::getSymbols.Finam('MICEX',from = "2001-01-01") # ммвб
chartSeries(MICEX, theme = 'white')

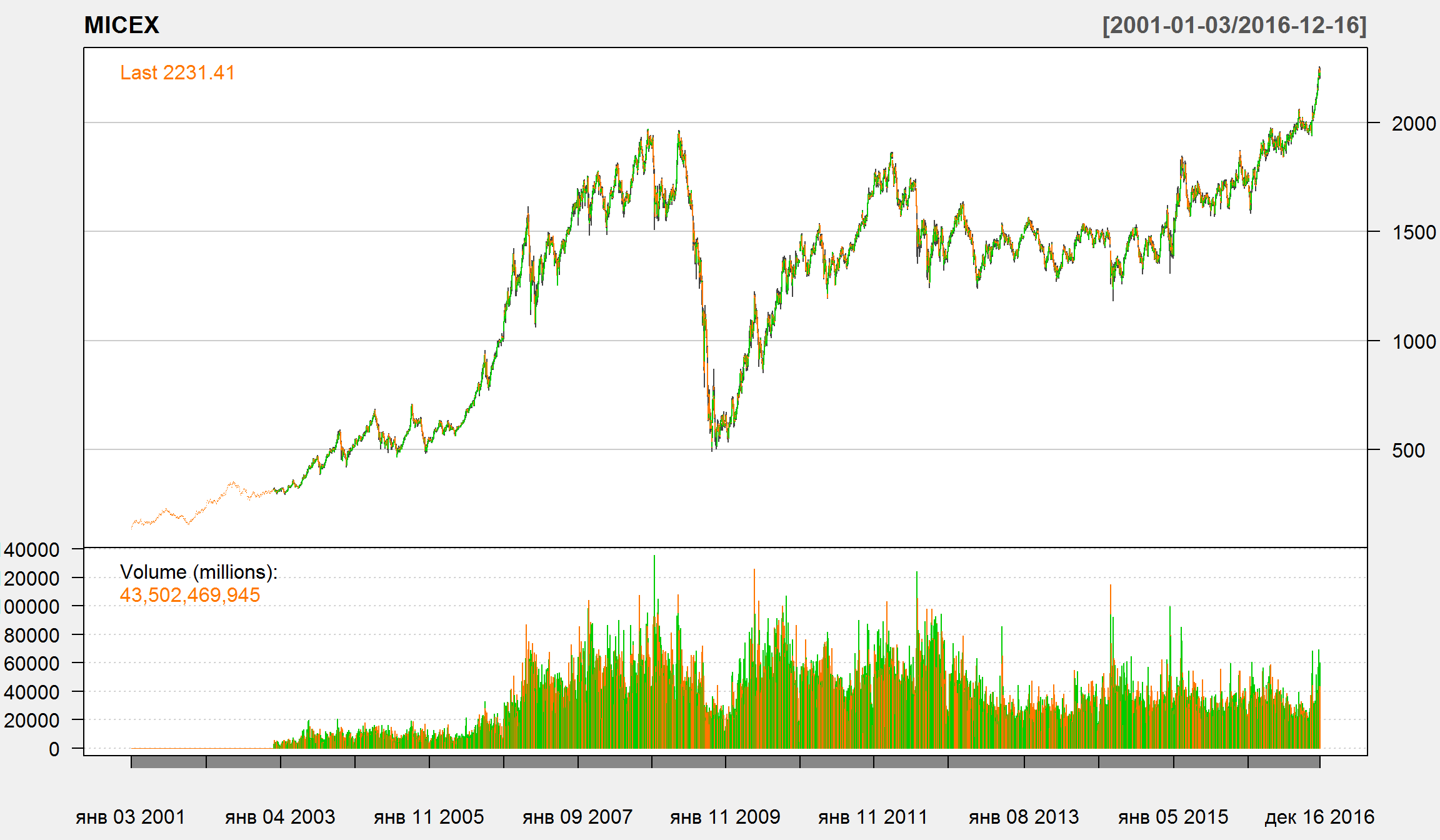
в логарифмах

log.MICEX <- log(MICEX$MICEX.Close)
plot(log.MICEX)

Acf(log.MICEX)

Pacf(log.MICEX)

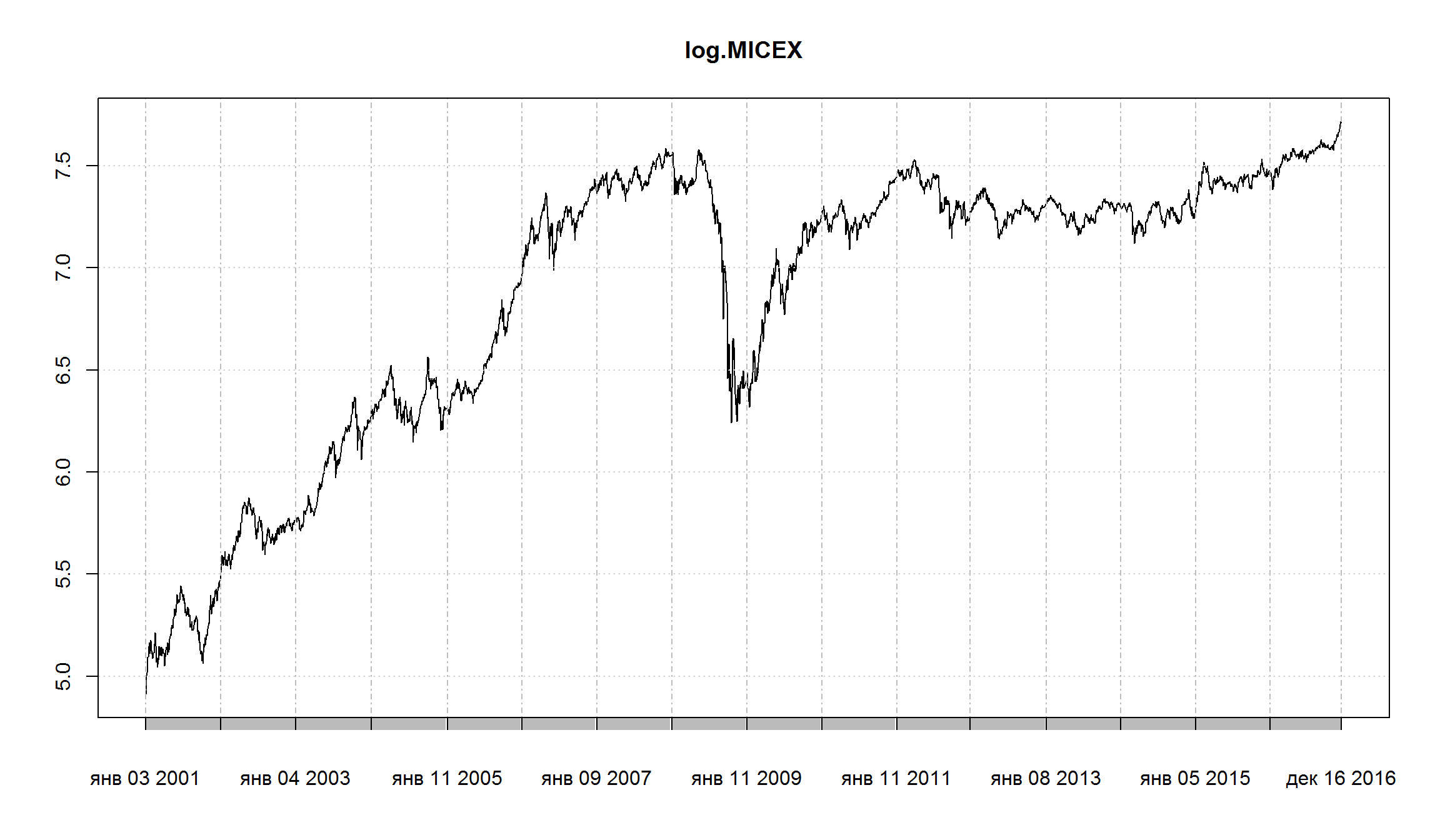
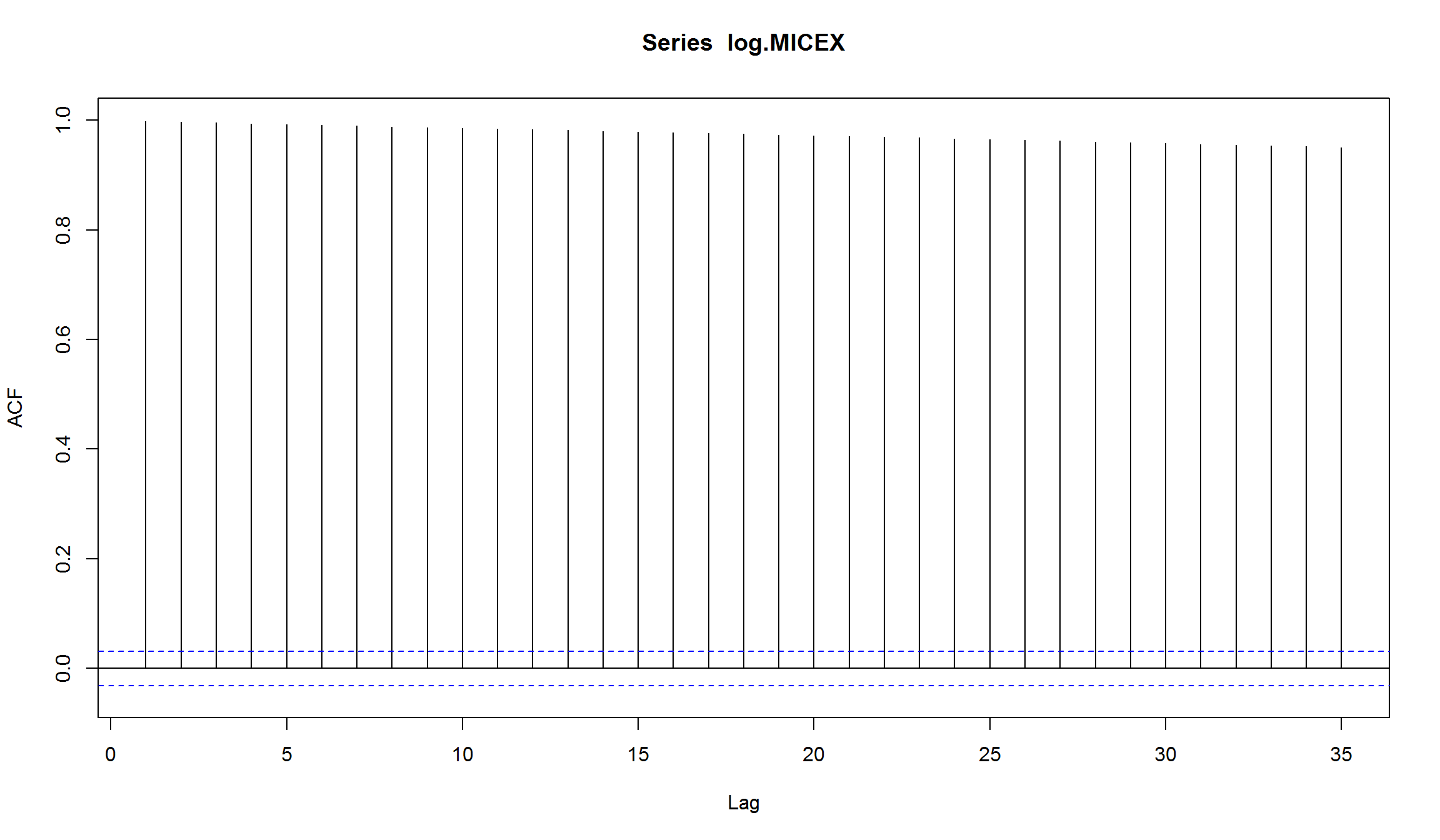
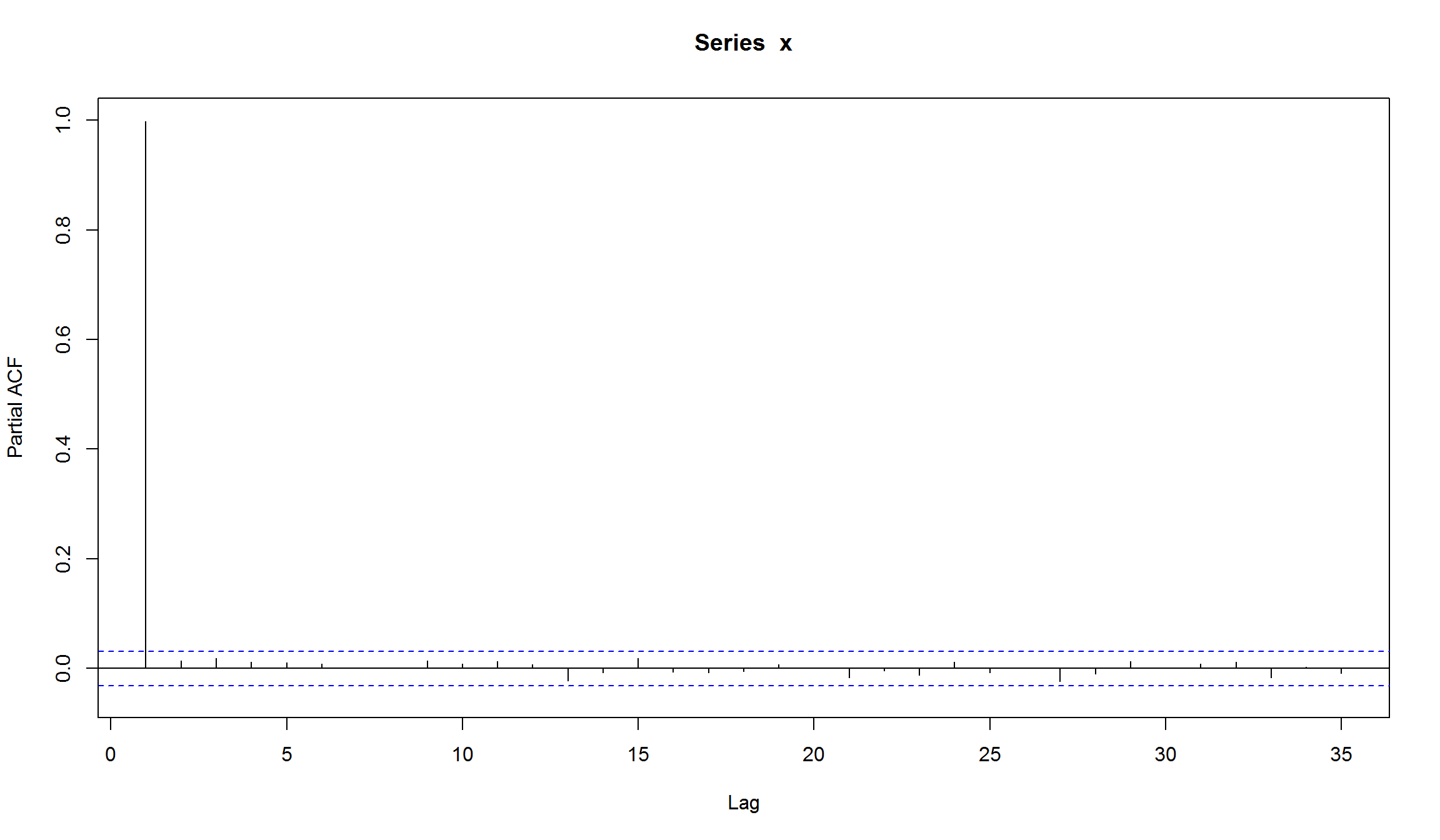
для лог-доходностей

diff.log.MICEX <- c(NA, diff(log.MICEX))
plot(diff.log.MICEX, type='l', col = 2)

Acf(diff.log.MICEX)

Pacf(diff.log.MICEX)

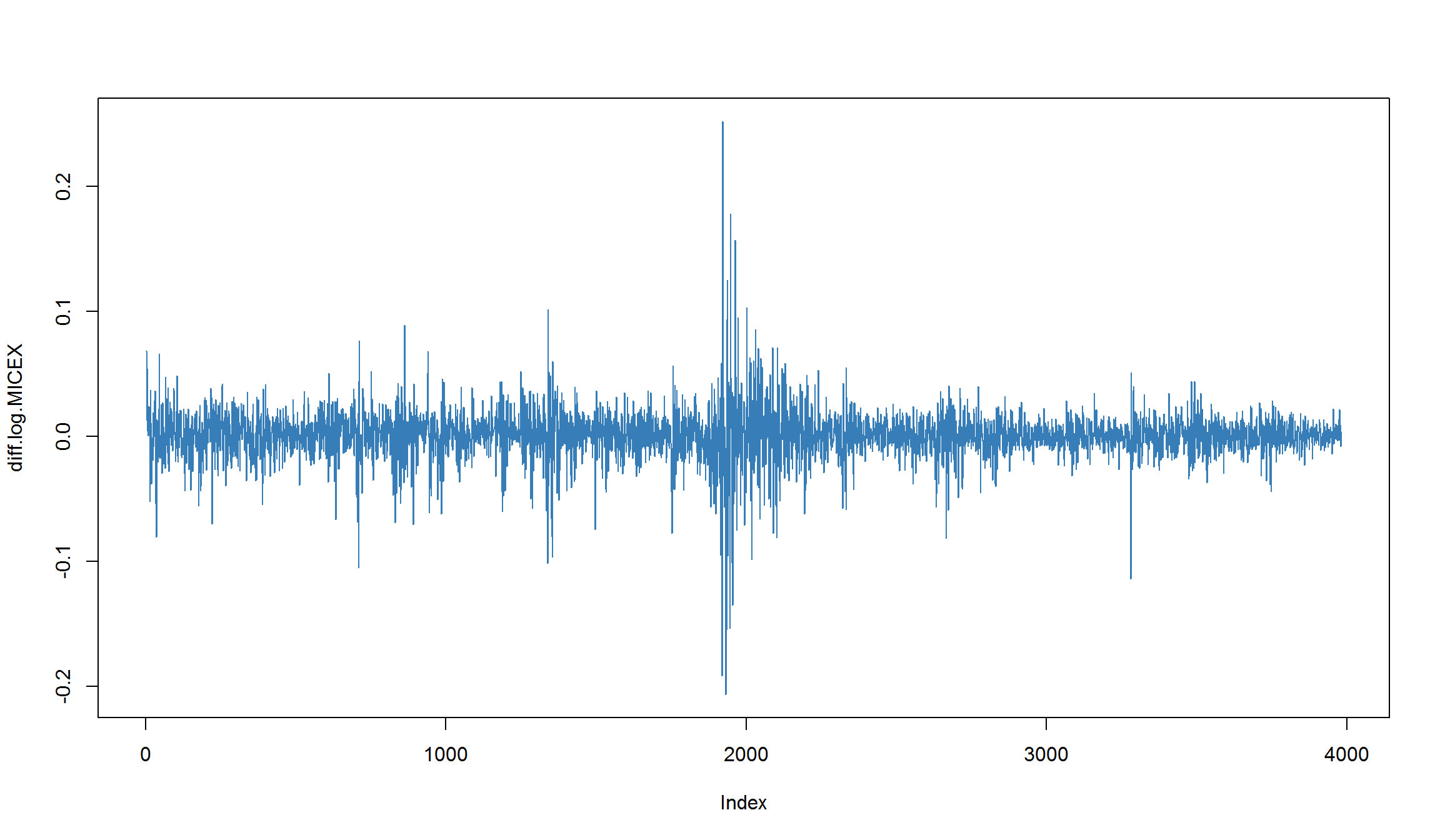
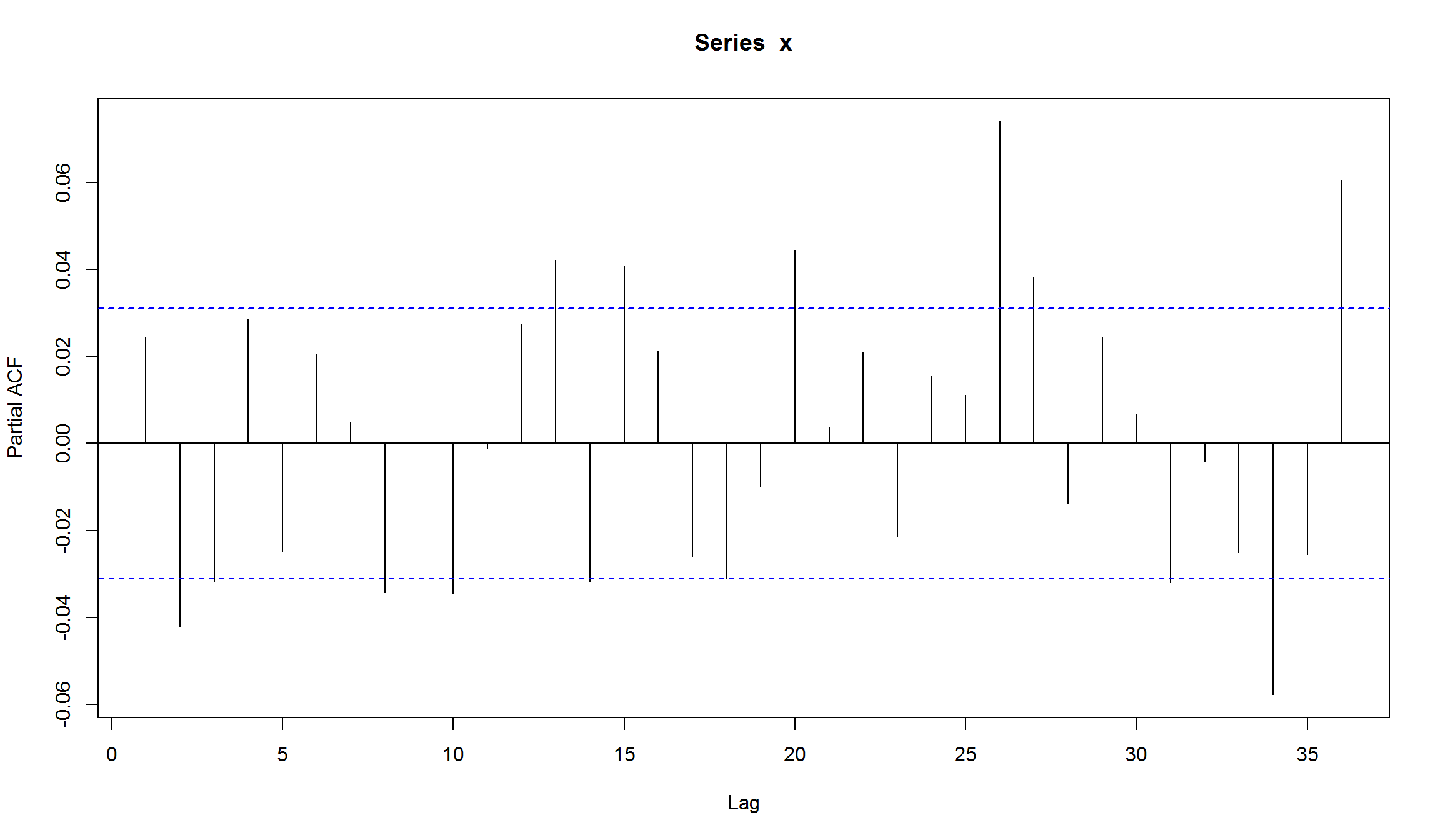
MA(1)-модель для индекса ММВБ

micex.ma <- Arima(diff.log.MICEX, order=c(0, 0, 1))
micex.ma

Series: diff.log.MICEX 
ARIMA(0,0,1) with non-zero mean 

Coefficients:
         ma1   mean
      0.0266  7e-04
s.e.  0.0165  3e-04

sigma^2 estimated as 0.0004229:  log likelihood=9811.81
AIC=-19617.62   AICc=-19617.61   BIC=-19598.75

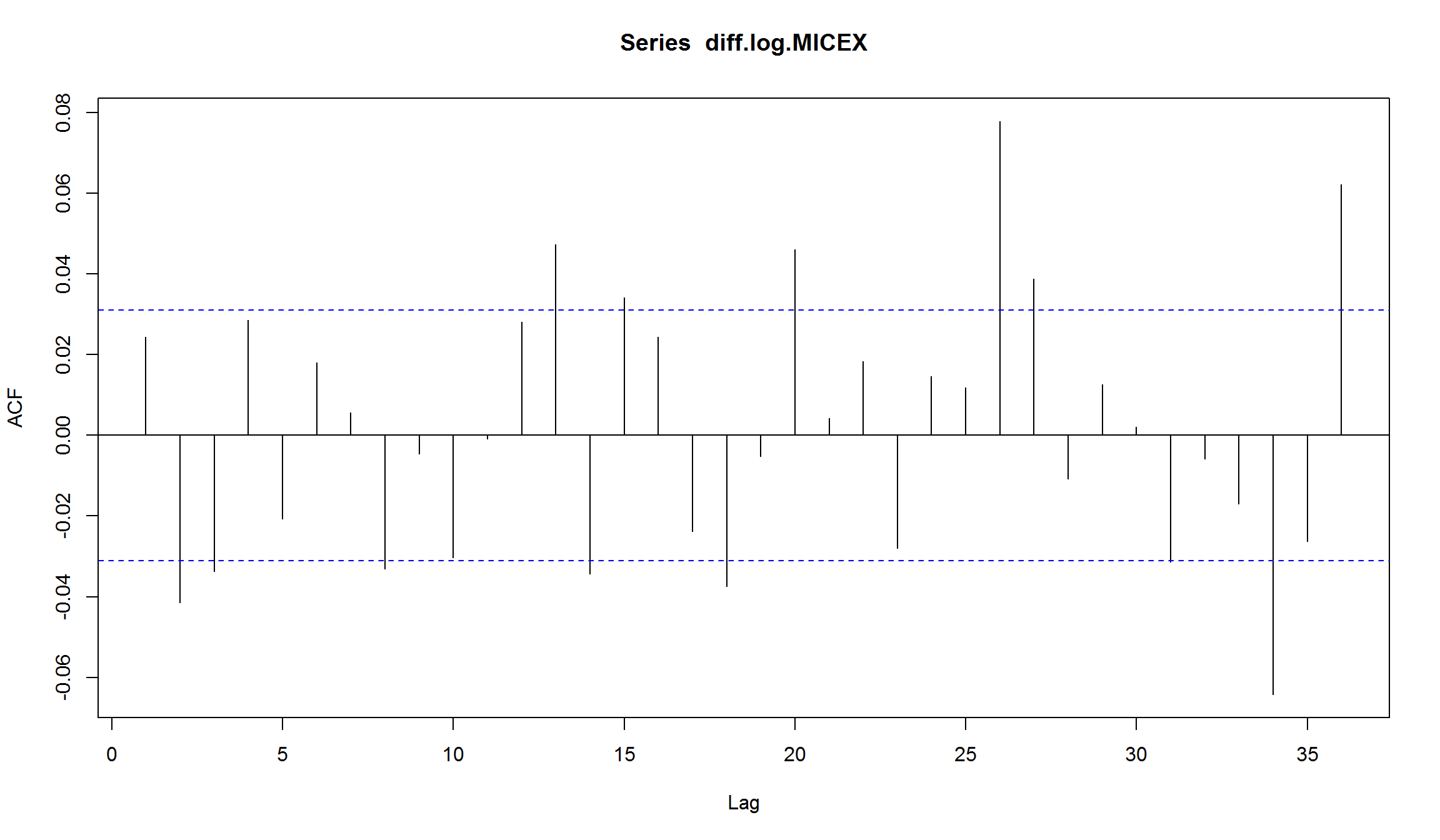
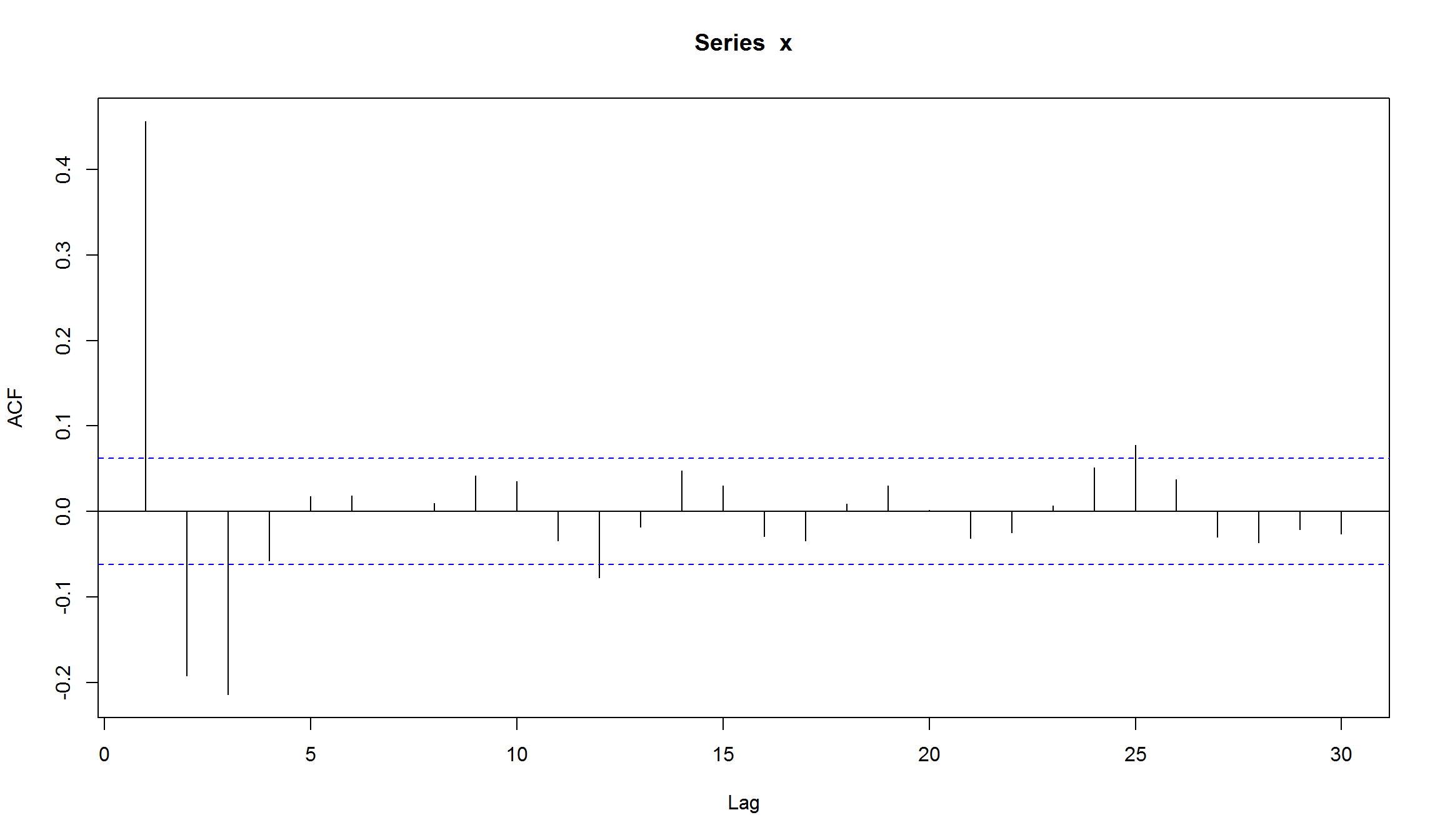
Acf(micex.ma$res[-(1:2)])

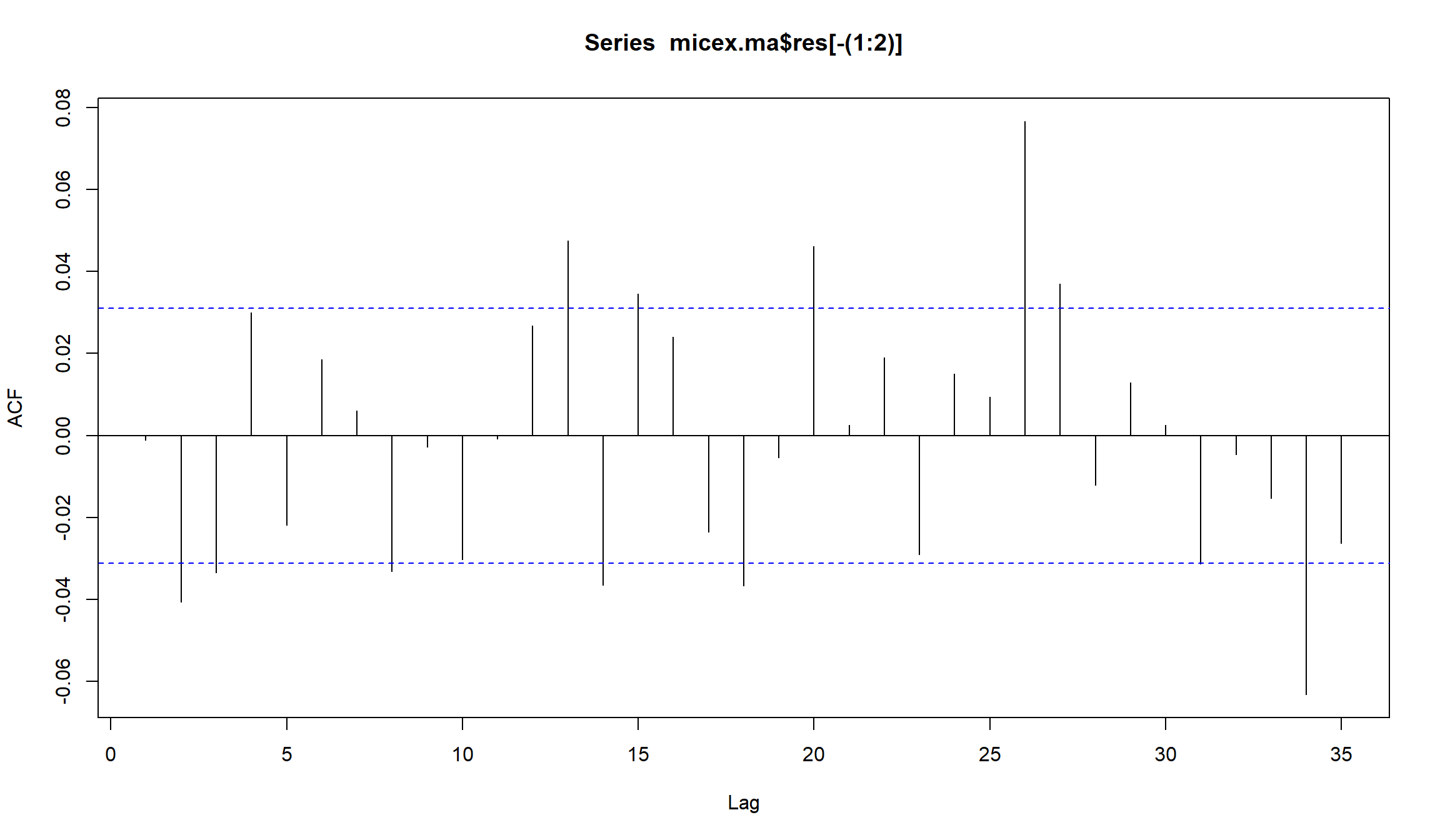
Остатки MA(1) для индекса ММВБ

• Остатки MA(1)-модели не являются белым шумом. В остатках сохраняется значимая автокорреляция на лагах 13,20,26,34.

Построим график остатков:

plot(micex.ma$residuals)

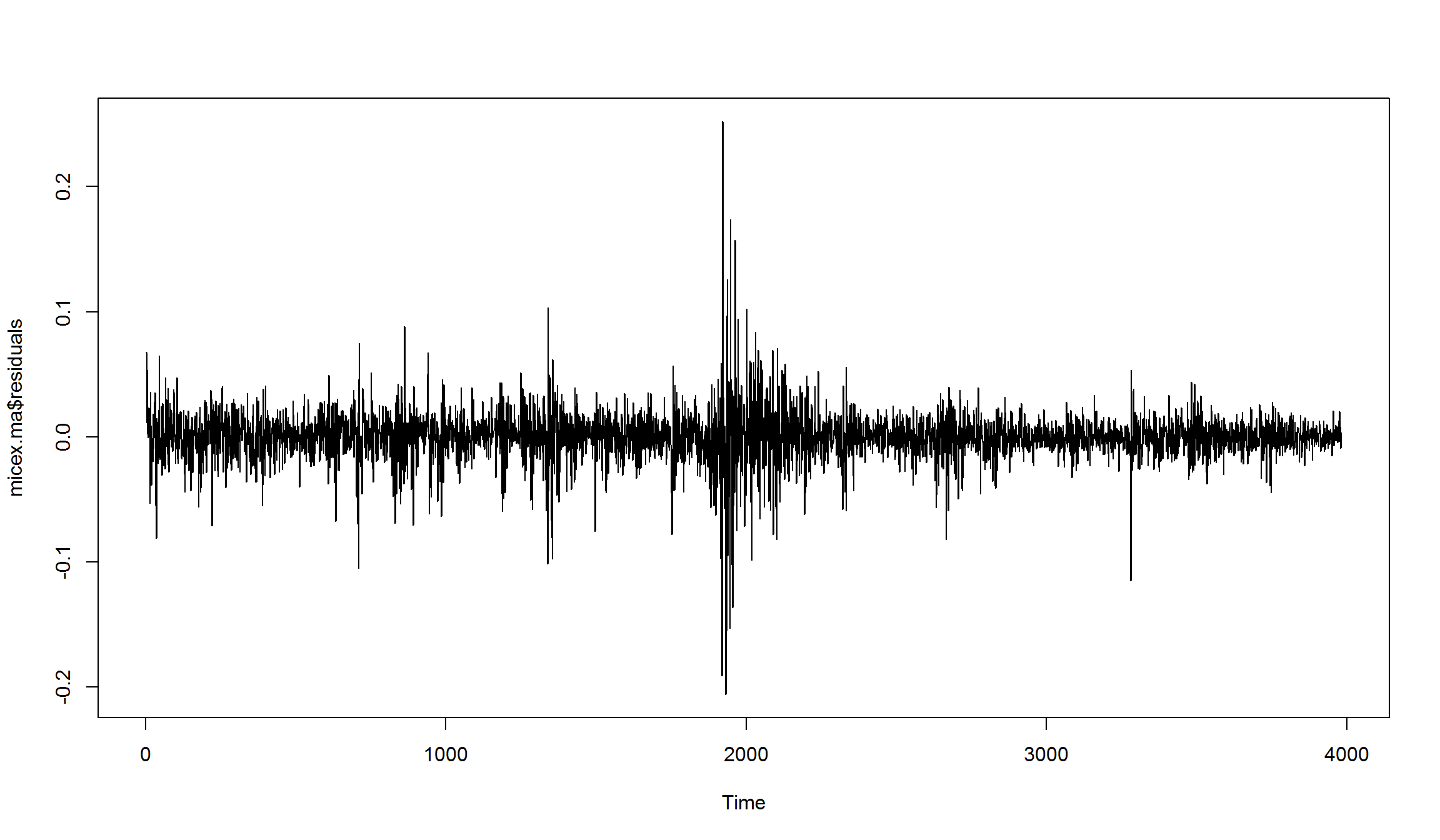
MA(2) для доходностей индекса ММВБ

попробуем оценить MA(2)-модель

micex.ma <- arima(diff.log.MICEX, order=c(0, 0, 2))
micex.ma

Call:
arima(x = diff.log.MICEX, order = c(0, 0, 2))

Coefficients:
         ma1      ma2  intercept
      0.0226  -0.0378      7e-04
s.e.  0.0159   0.0154      3e-04

sigma^2 estimated as 0.0004222:  log likelihood = 9814.8,  aic = -19621.6

acf(micex.ma$res[-(1:2)])

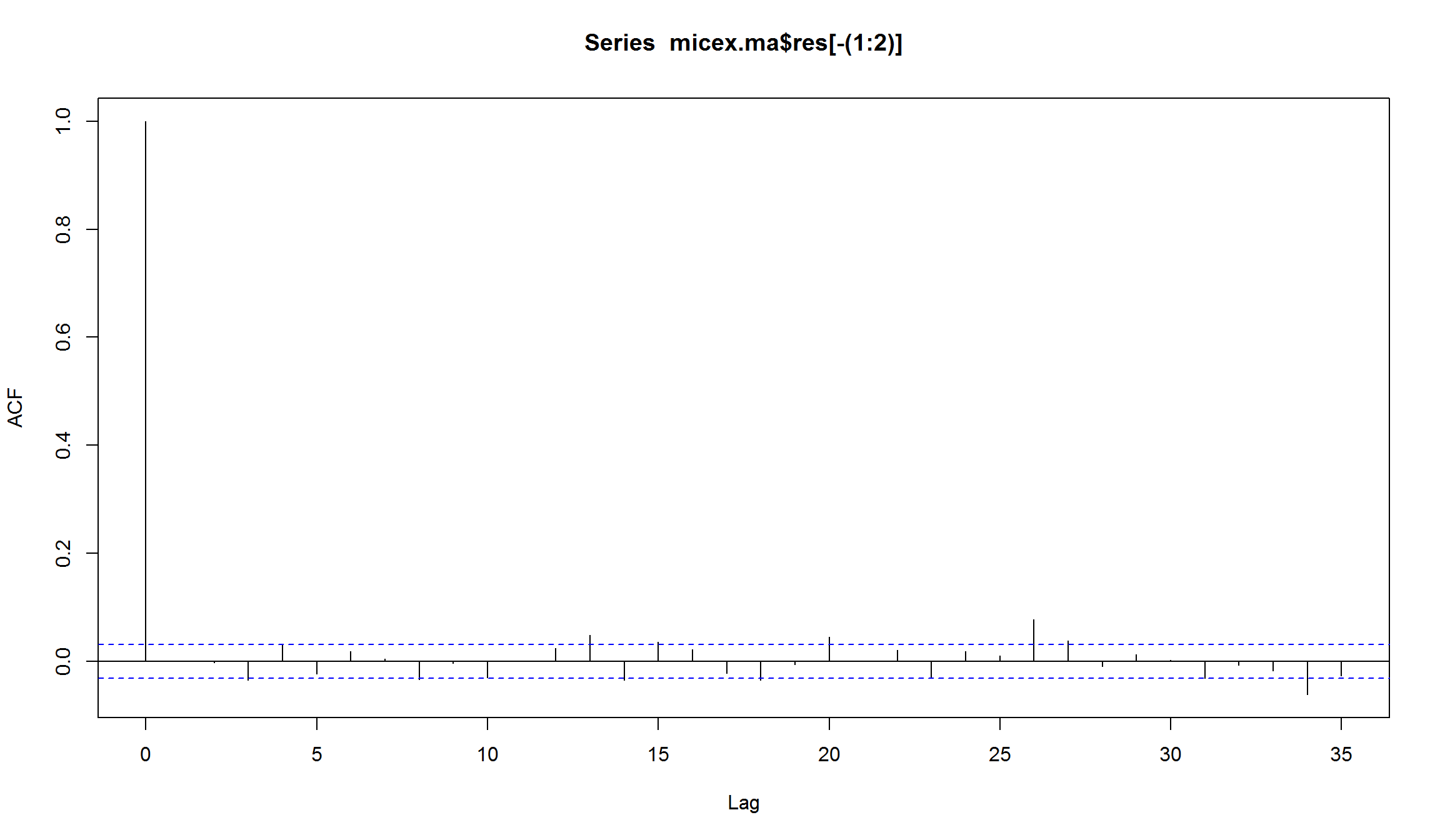
• MA(2)-модель позволила “убрать” автокорреляцию на лаге 2, но автокорреляция на других лагах сохранилась.

MA(3)-модель для индекса ММВБ

попробуем оценить MA(3)-модель

micex.ma <- arima(diff.log.MICEX, order=c(0, 0, 3))
micex.ma

Call:
arima(x = diff.log.MICEX, order = c(0, 0, 3))

Coefficients:
         ma1      ma2      ma3  intercept
      0.0263  -0.0401  -0.0363      7e-04
s.e.  0.0159   0.0154   0.0157      3e-04

sigma^2 estimated as 0.0004217:  log likelihood = 9817.46,  aic = -19624.91

acf(micex.ma$res[-(1:2)])

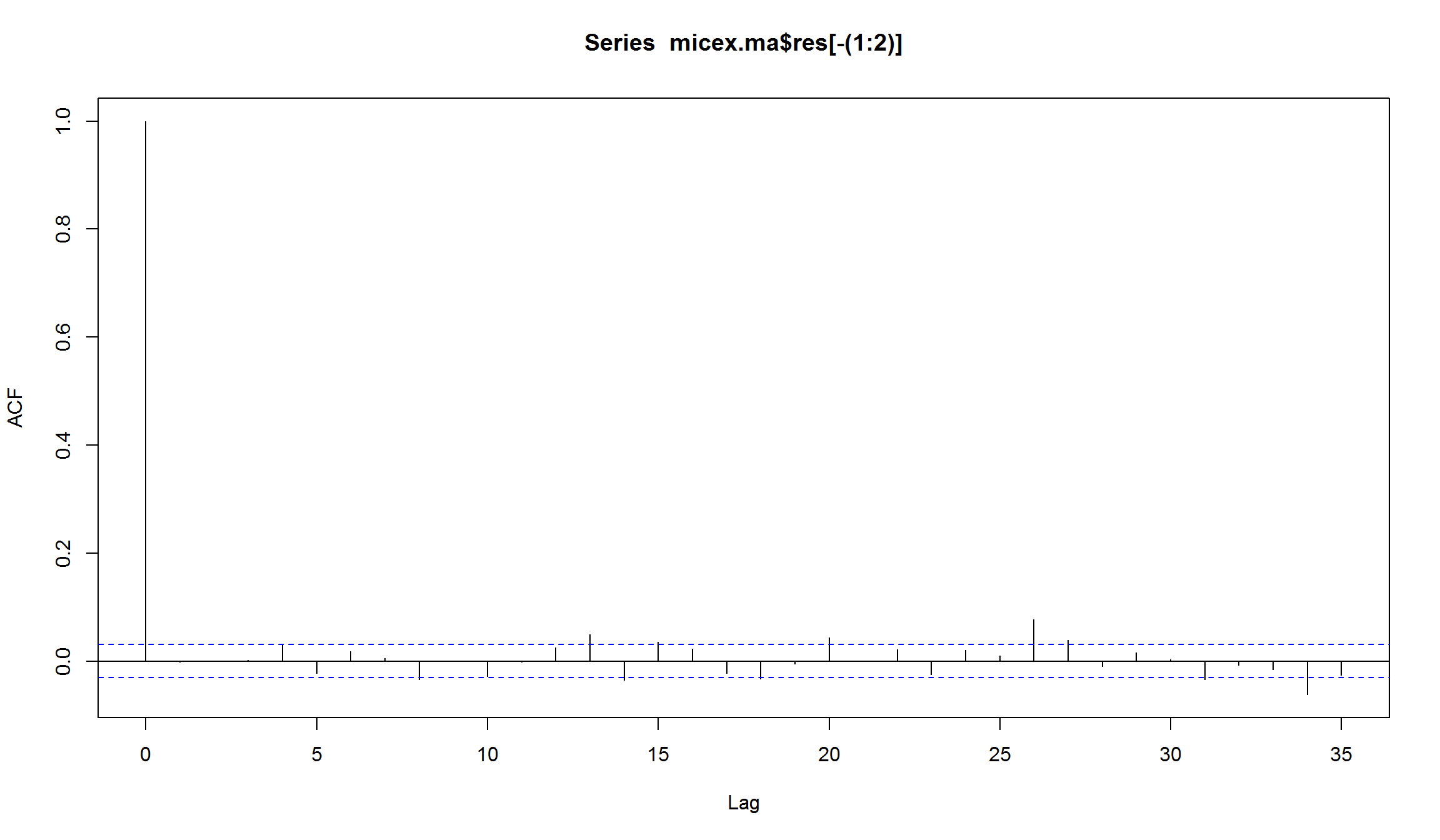
• Построение MA(3)-модели не позволило улучшить автокоррелограмму.

Выводы по AR и MA моделям

• Оба типа моделей - AR и MA - позволяют частично объяснять автокорреляцию в сериях лог-доходностей акций.
• Однако кластеризация волатильности и эффекты “длинной памяти” все же остаются в остатках.
• Может ли объединение двух подходов улучшить ситуацию?

Информационные критерии

• Информационные критерии – это инструменты, которые помогают нам выбирать “лучшие” модели. Информационный критерий оценивает “качество” модели по сравнению с альтернативными спецификациями модели.
• Чаще всего используются два критерия - критерий Акаике (AIC) и Байесовский информационный критерий (BIC).
• Общая идея всех информационных критериев заключается в оценке баланса между прогностический точностью модели и ее сложностью.
• Мы хотим строить минимально сложные модели (“бритва Оккама”), но которые при этом имели максимальную объясняющую способность

Информационный критерий Акаике

Если мы используем функцию правдоподобия (likelyhood function) для оценки модели c \(k\) параметрами и значение \(L\) максимизирует функцию правдоподобия, то AIC рассчитывается как:

\[ AIC = -2log(L) + 2k \]

• Мы предпочитаем модели, которые имеют минимальное значение AIC.
• Как видно из формулы, AIC увеличивается по мере роста количества параметров (k) и снижается по мере роста log-likelyhood (L), то есть точности оценки
• Абсолютные значения AIC не имеют значения, мы сравниваем только значения AIC для различных моделей, которые построены на одних данных.
• Значения информационных критериев для разных серий не сравнимы между собой!

Байесовский информационный критерий (BIC)

BIC рассчитывается как:

\[ BIC = -2log(L) + k log(n) \] где \(n\) - количество наблюдений в рассматриваемой серии.

• AIC и BIC могут указывать на разные модели как “лучшие” и противоречить друг другу
• Можно использовать AIC как более предпочтительный критерий

ARMA-модели

• AR-модели учитывают прошлое поведение (лаги) в качестве входных параметров. С сутевой точки зрения это позволяет учитывать некоторые особенности поведения участников финансового рынка рынка, такое как mean reversion (возвращение к среднему) или momentum (инерционность финансовых рынков – после роста сохраняется тенденция к росту, и – наоборот).
• MA-модели используются для оценки “информационных шоков” в серии. К примеру, такими шоками могут быть неожиданные события или поступление новой информации (выход квартальной финансовой отчетности) и так далее. То есть, MA-модель позволяет оценивать единовременную реакцию серии на шоки.
  
• ARMA-модели учитывают оба этих аспекта при моделировании финансовых серий.
• ARMA-модели в принципе не учитывают эффекты “кластеризации волатильности”. Это не условные гетероскедастичные модели. Мы считаем, что дисперсия является постоянной в ARMA-моделях.

Определение ARMA-модели

Если серия временного ряда \({x_t}\) является моделью ARMA(p,q), то

\[ x_t = \alpha_1 x_{t-1} + \alpha_2 x_{t-2} + \ldots + w_t + \beta_1 w_{t-1} + \beta_2 w_{t-2} + \ldots + \beta_q w_{t-q} \]

• Основное преимущество ARMA-модели по сравнению c AR или MA, заключается в том, что как правило она требует меньше параметров для оценки.
• Вспомните, что AR-модели на настоящих данных требовали оценки коэффициентов для 20-30 лагов.

Симулирование ARMA(1,1)

Простейшая ARMA-модель – это ARMA(1,1). Модель имеет вид:

\[x_t + \alpha x_{t-1} + w_t + \beta w_{t-1} \]

set.seed(123)
x <- arima.sim(n=1000, model=list(ar=0.5, ma=-0.5))
plot(x)

Acf(x)

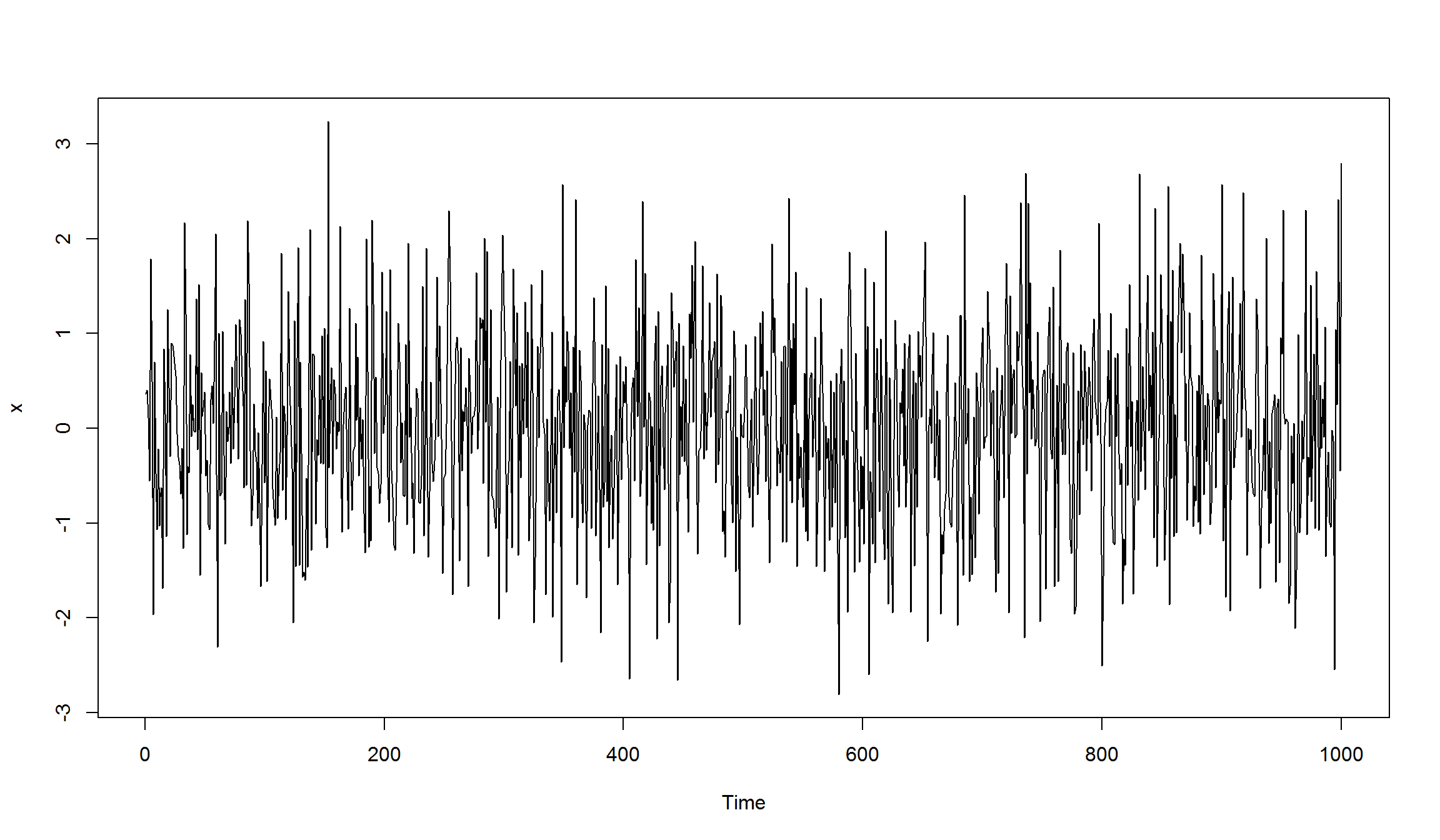
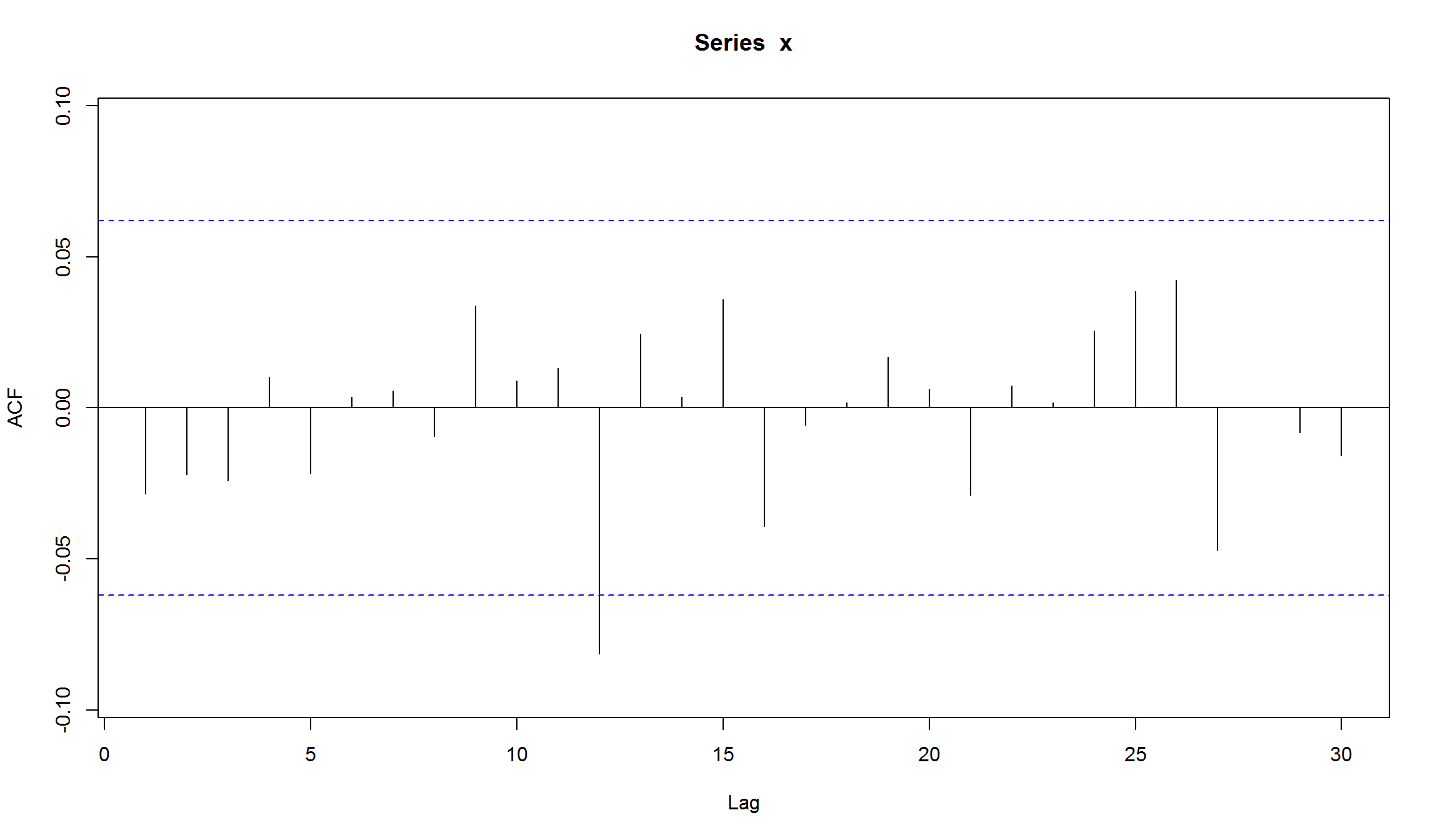
• Модель не имеет значимых автокорреляция на всех лагах

оценим симулированную модель:

arima(x, order=c(1, 0, 1))

Warning in arima(x, order = c(1, 0, 1)): possible convergence problem:
optim gave code = 1

Call:
arima(x = x, order = c(1, 0, 1))

Coefficients:
         ar1      ma1  intercept
      0.5997  -0.6334     0.0158
s.e.  0.3777   0.3658     0.0289

sigma^2 estimated as 0.9951:  log likelihood = -1416.46,  aic = 2840.93

Симулирование ARMA(2,2)

set.seed(123)
x <- arima.sim(n=1000, model=list(ar=c(0.5, -0.25), ma=c(0.5, -0.3)))
plot(x)

Acf(x)

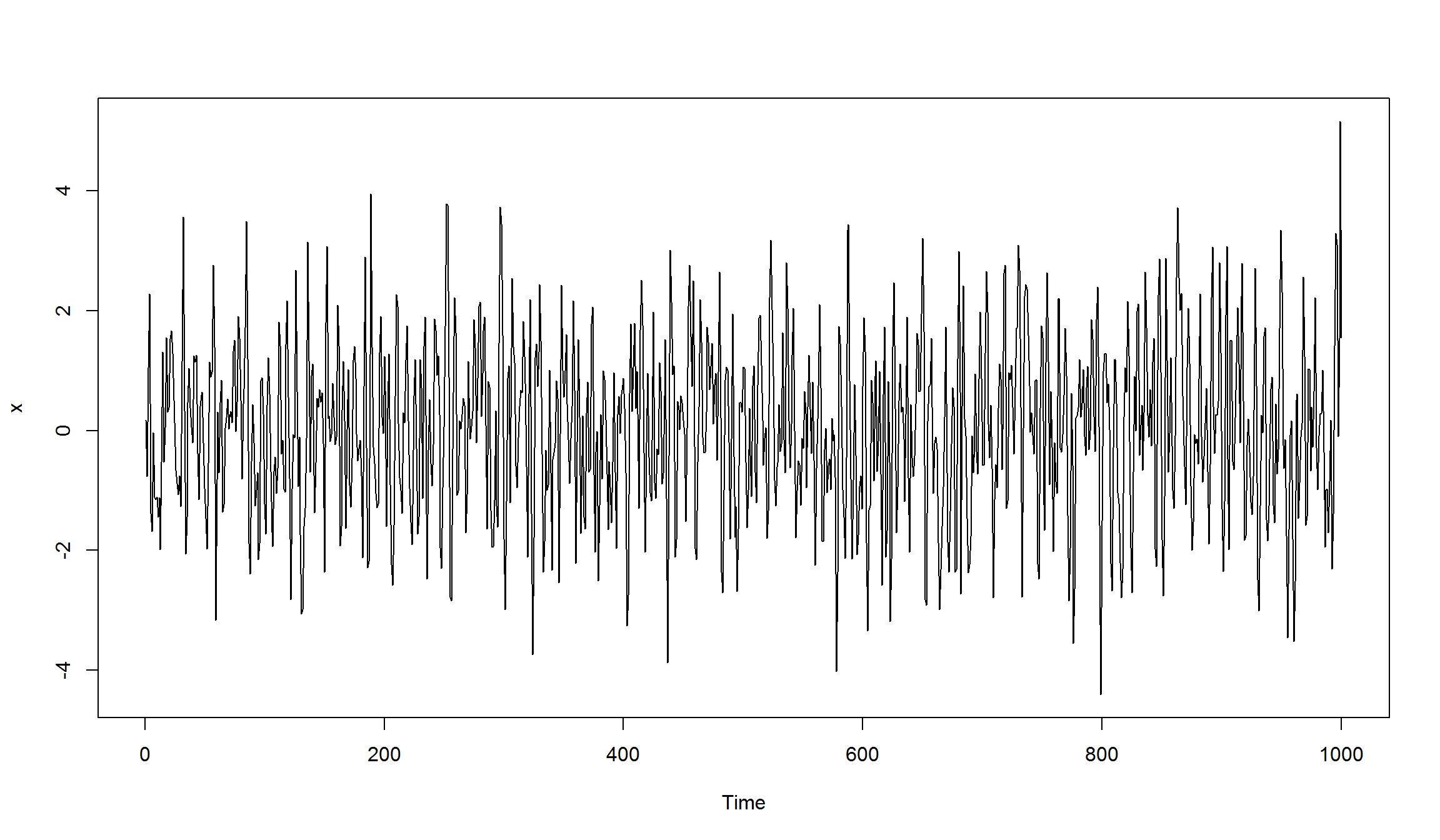
оценим модель

Arima(x, order=c(2, 0, 2))

Series: x 
ARIMA(2,0,2) with non-zero mean 

Coefficients:
         ar1      ar2     ma1      ma2  intercept
      0.5099  -0.2693  0.4636  -0.3309     0.0269
s.e.  0.1157   0.0346  0.1190   0.1122     0.0473

sigma^2 estimated as 1.009:  log likelihood=-1422.06
AIC=2856.13   AICc=2856.21   BIC=2885.58

confint(arima(x, order=c(2, 0, 2)))

                2.5 %     97.5 %
ar1        0.28315655  0.7366981
ar2       -0.33701341 -0.2015434
ma1        0.23045772  0.6968166
ma2       -0.55079028 -0.1110161
intercept -0.06574923  0.1196155

• Доверительные интервалы содержат настоящие значения параметров ar=c(0.5, -0.25), ma=c(0.5, -0.3), но являются достаточно широкими

Построение ARMA-моделей

Построим несколько моделей для доходностей индекса ММВБ

# без константы (сводобного члена)
fit.00 <- Arima(diff.log.MICEX, c(0, 0, 0), include.drift=FALSE)
fit.01 <- Arima(diff.log.MICEX, c(0, 0, 1), include.drift=FALSE)
fit.02 <- Arima(diff.log.MICEX, c(0, 0, 2), include.drift=FALSE)
fit.10 <- Arima(diff.log.MICEX, c(1, 0, 0), include.drift=FALSE)
fit.11 <- Arima(diff.log.MICEX, c(1, 0, 1), include.drift=FALSE)
fit.12 <- Arima(diff.log.MICEX, c(1, 0, 2), include.drift=FALSE)
fit.20 <- Arima(diff.log.MICEX, c(2, 0, 0), include.drift=FALSE)
fit.21 <- Arima(diff.log.MICEX, c(2, 0, 1), include.drift=FALSE)
fit.22 <- Arima(diff.log.MICEX, c(2, 0, 2), include.drift=FALSE)

# с константой 
fit.00c <- Arima(diff.log.MICEX, c(0, 0, 0), include.drift=TRUE)
fit.01c <- Arima(diff.log.MICEX, c(0, 0, 1), include.drift=TRUE)
fit.02c <- Arima(diff.log.MICEX, c(0, 0, 2), include.drift=TRUE)
fit.10c <- Arima(diff.log.MICEX, c(1, 0, 0), include.drift=TRUE)
fit.11c <- Arima(diff.log.MICEX, c(1, 0, 1), include.drift=TRUE)
fit.12c <- Arima(diff.log.MICEX, c(1, 0, 2), include.drift=TRUE)
fit.20c <- Arima(diff.log.MICEX, c(2, 0, 0), include.drift=TRUE)
fit.21c <- Arima(diff.log.MICEX, c(2, 0, 1), include.drift=TRUE)
fit.22c <- Arima(diff.log.MICEX, c(2, 0, 2), include.drift=TRUE)

# аггрегируем результаты
models <- data.frame(p = rep(c(0, 0, 0, 1, 1, 1, 2, 2, 2), 2),
                     d = rep(0, 18),
                     q = rep(c(0, 1, 2), 6),
                     include.drift = c(rep(FALSE, 9), rep(TRUE, 9)),
                     loglik = c(fit.00$loglik, fit.01$loglik, fit.02$loglik,
                                fit.10$loglik, fit.11$loglik, fit.12$loglik,
                                fit.20$loglik, fit.21$loglik, fit.22$loglik,
                                fit.00c$loglik, fit.01c$loglik, fit.02c$loglik,
                                fit.10c$loglik, fit.11c$loglik, fit.12c$loglik,
                                fit.20c$loglik, fit.21c$loglik, fit.22c$loglik),
                     aicc = c(fit.00$aicc, fit.01$aicc, fit.02$aicc,
                                fit.10$aicc, fit.11$aicc, fit.12$aicc,
                                fit.20$aicc, fit.21$aicc, fit.22$aicc,
                                fit.00c$aicc, fit.01c$aicc, fit.02c$aicc,
                                fit.10c$aicc, fit.11c$aicc, fit.12c$aicc,
                                fit.20c$aicc, fit.21c$aicc, fit.22c$aicc),
                      bic = c(fit.00$bic, fit.01$bic, fit.02$bic,
                                fit.10$bic, fit.11$bic, fit.12$bic,
                                fit.20$bic, fit.21$bic, fit.22$bic,
                                fit.00c$bic, fit.01c$bic, fit.02c$bic,
                                fit.10c$bic, fit.11c$bic, fit.12c$bic,
                                fit.20c$bic, fit.21c$bic, fit.22c$bic)
                     )
print(models, digits=6)

   p d q include.drift  loglik     aicc      bic
1  0 0 0         FALSE 9810.52 -19617.0 -19604.5
2  0 0 1         FALSE 9811.81 -19617.6 -19598.8
3  0 0 2         FALSE 9814.80 -19621.6 -19596.4
4  1 0 0         FALSE 9811.70 -19617.4 -19598.5
5  1 0 1         FALSE 9812.51 -19617.0 -19591.9
6  1 0 2         FALSE 9815.93 -19621.8 -19590.4
7  2 0 0         FALSE 9815.25 -19622.5 -19597.3
8  2 0 1         FALSE 9816.19 -19622.4 -19590.9
9  2 0 2         FALSE 9816.78 -19621.5 -19583.8
10 0 0 0          TRUE 9811.66 -19617.3 -19598.5
11 0 0 1          TRUE 9812.90 -19617.8 -19592.6
12 0 0 2          TRUE 9815.97 -19621.9 -19590.5
13 1 0 0          TRUE 9812.79 -19617.6 -19592.4
14 1 0 1          TRUE 9813.61 -19617.2 -19585.8
15 1 0 2          TRUE 9817.15 -19622.3 -19584.6
16 2 0 0          TRUE 9816.43 -19622.8 -19591.4
17 2 0 1          TRUE 9817.41 -19622.8 -19585.1
18 2 0 2          TRUE 9817.98 -19621.9 -19577.9

Лучшая модель по AIC

выберем “лучшую” модель по критерию Акаике

library(ggplot2)
models$descr <- paste(models$p, models$q, models$include.drift)
p <- ggplot(models, aes(descr,aicc))
p + geom_point()+coord_flip()+theme_minimal()

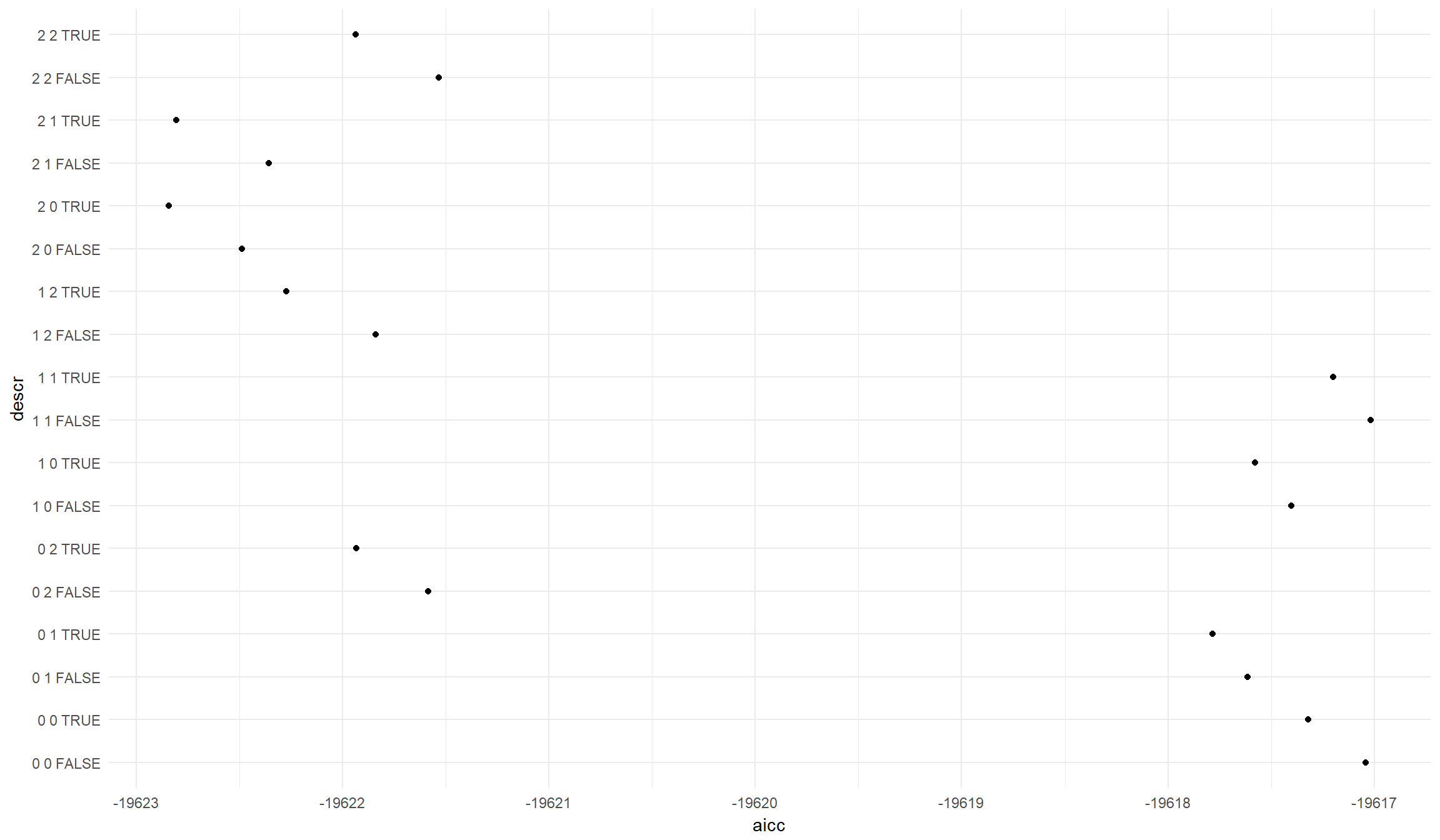
models[which(models$aicc == min(models$aicc)),]

   p d q include.drift   loglik      aicc       bic    descr
16 2 0 0          TRUE 9816.429 -19622.84 -19591.41 2 0 TRUE

какая модель минимизирует AIC?

Оценка “лучшей” модели (AIC)

выбрали “вторую” лучшую модель по критерию AIC

fit.best <- Arima(diff.log.MICEX, c(2, 0, 0), include.drift=TRUE)
print(fit.best)

Series: diff.log.MICEX 
ARIMA(2,0,0) with drift         

Coefficients:
         ar1      ar2  intercept  drift
      0.0249  -0.0428     0.0016      0
s.e.  0.0159   0.0159     0.0006      0

sigma^2 estimated as 0.0004221:  log likelihood=9816.43
AIC=-19622.86   AICc=-19622.84   BIC=-19591.41

Остатки модели ARMA

resid <- residuals(fit.best)
plot(resid, type="l", col=2)

Acf(resid)

Pacf(resid)

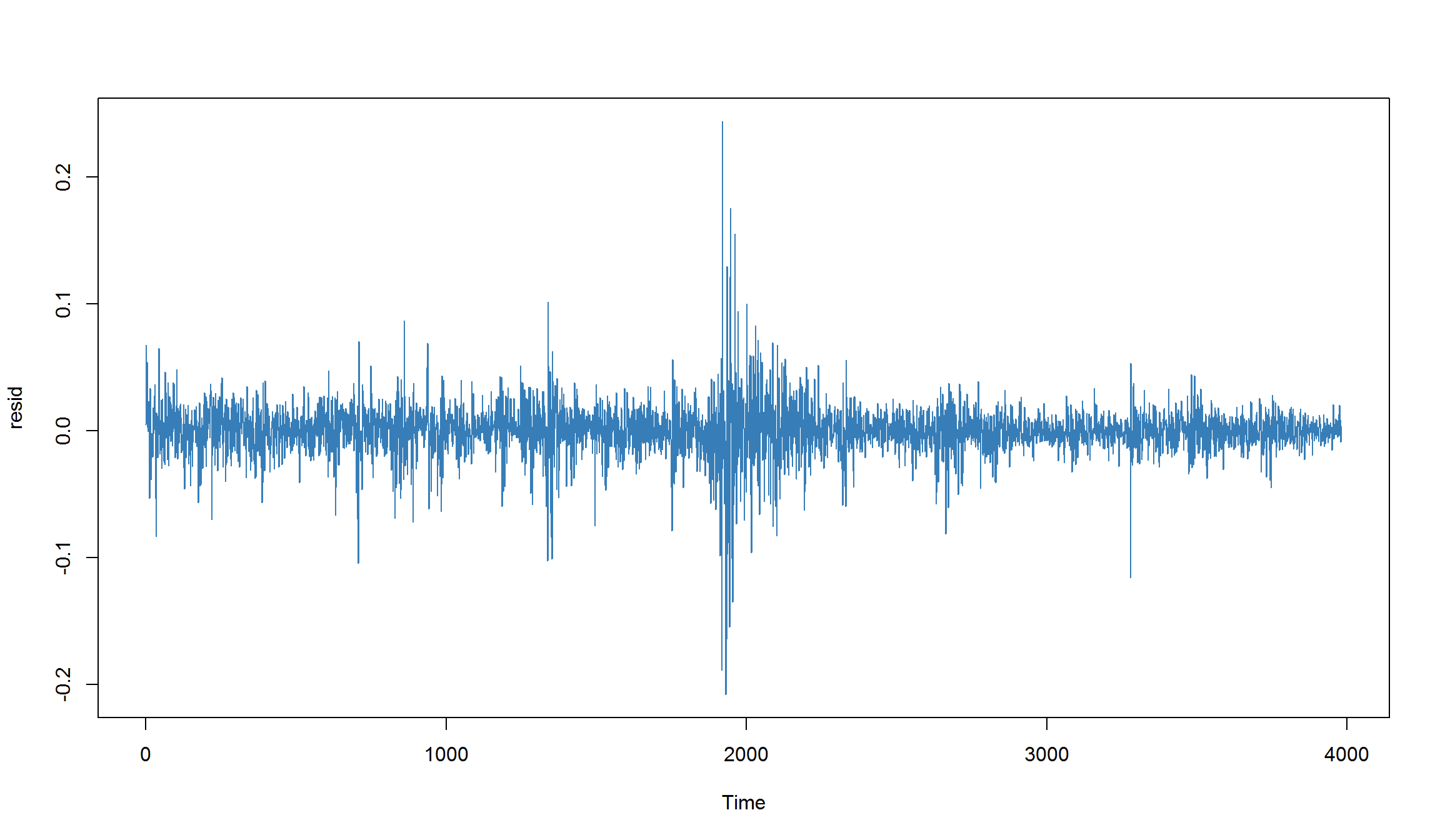
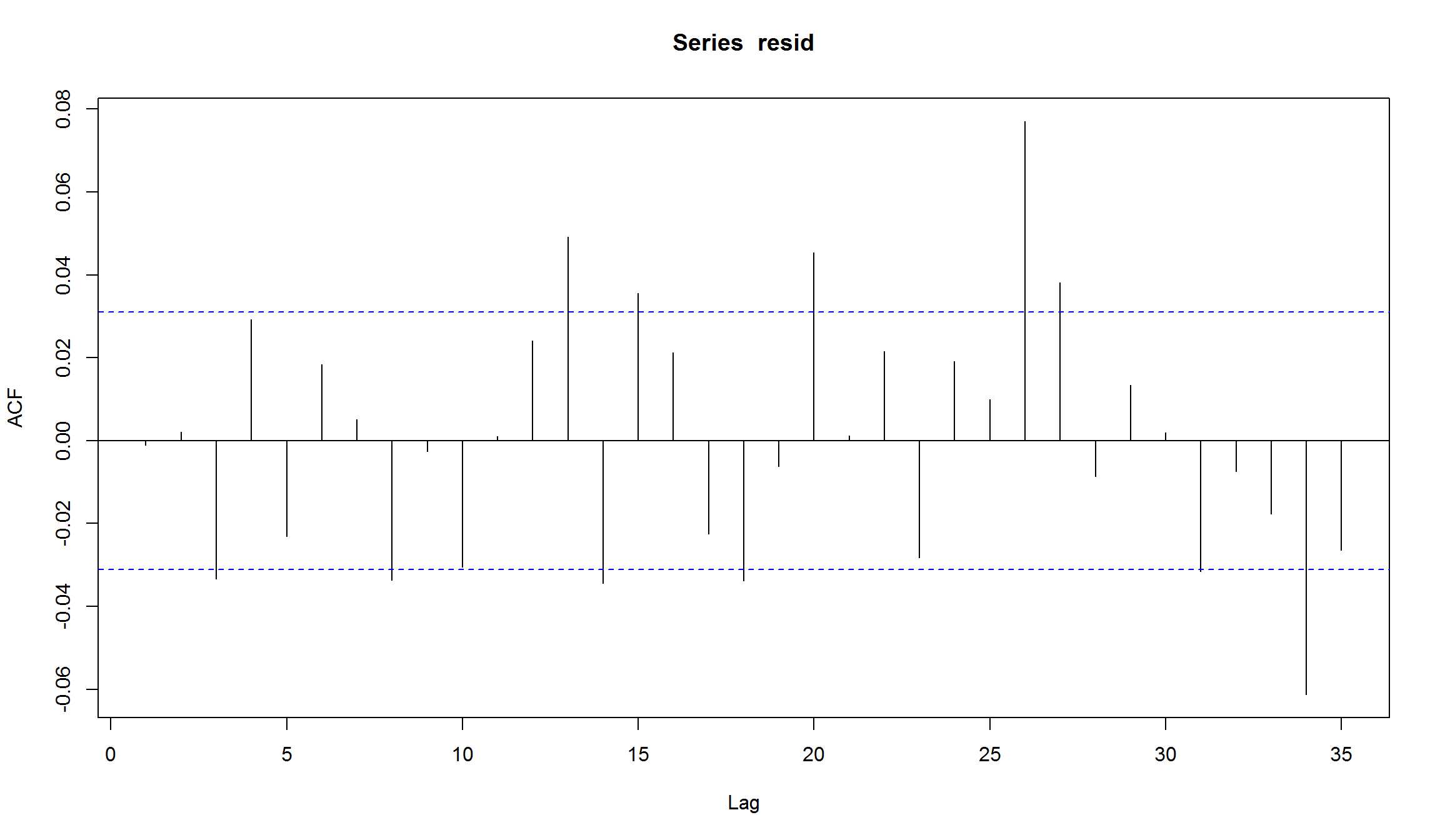
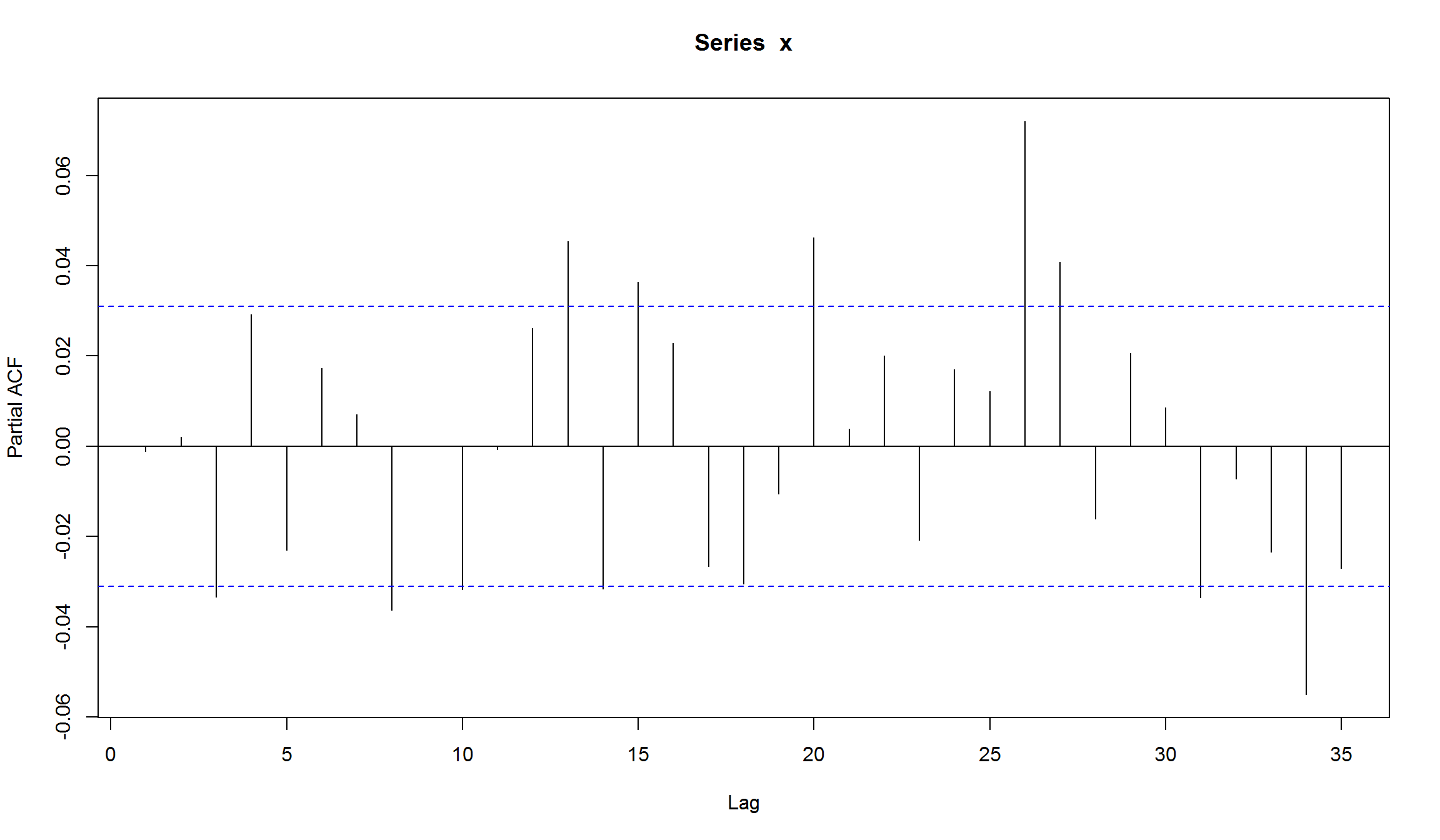
• даже в “лучшей” модели ARMA сохранилась автокорреляция в остатках

Cтатистика Ljung-Box

• Статистика Ljung-Box является классическим тестом на гипотезу о том, что набор автокорреляций в модели совместно отличается от 0.
• Тест не оценивает каждый индивидуальный лаг на отличие от 0, а оценивает совокупность лагов одновременно.
• \(H0\): серия на каждом лаге является i.i.d., то есть корреляции между между лагами равны нулю
• \(H1\): серия на каждом лаге не является i.i.d., то есть в ней сохраняется автокорреляция

Формально тест рассчитывает следующую статистику:

\[ Q = n(n+2) \sum_{k=1}^{h} \frac{\hat{\rho}^2}{n-k} \]

где \(n\) – количество наблюдений, \(\hat{\rho}^2\) – выборочная автокорреляция на лаге \(k\), \(h\) – тестируемый лаг.

• Мы отвергаем нулевую гипотезу \(H0\), если \(Q > \chi^2_{a,h}\) (для распределения хи-квадрат с \(h\) степенями свободы).
• Мы можем не вдаваться в подробности оценки, а использовать функцию Box.test для проведения теста:

Box.test(resid, lag=10, type = "Ljung-Box", fitdf=3)

    Box-Ljung test

data:  resid
X-squared = 19.738, df = 7, p-value = 0.006165

• если мы используем тест на остатках модели, то необходимо скорректировать количество степеней свободы (fitdf)
• fitdf = p +q и тестируемые лаги (lag) должны быть больше fitdf
• Тест указывает на сохранение автокорреляции в остатках модели

Построение прогноза

Для построения прогноза необходимо использовать функцию forecast из одноименного пакета:

plot(forecast(fit.best, h=100, level=95, fan = TRUE), col=2)

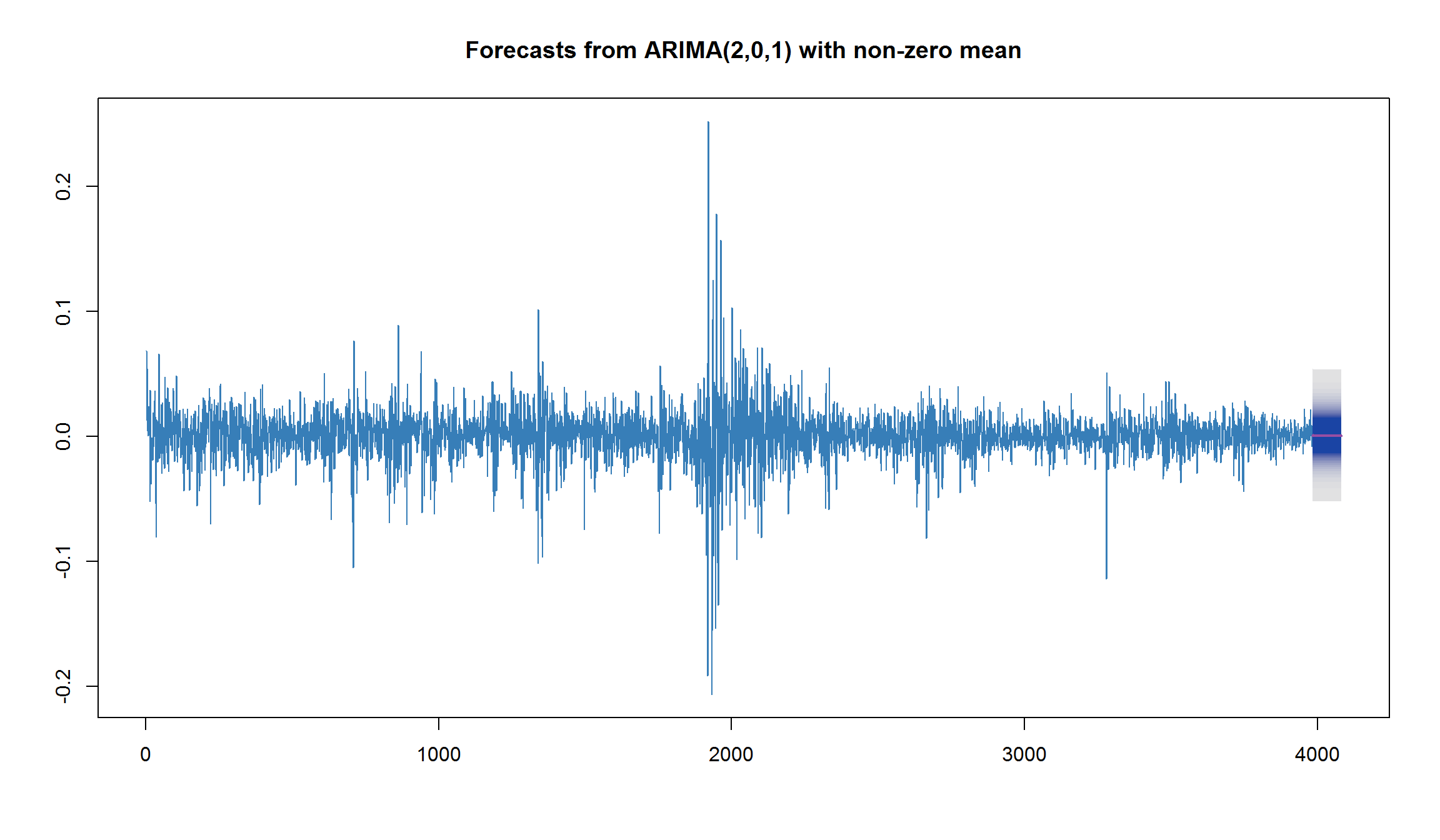
• h – определяет длину прогноза
• level – определяет доверительные интервалы для интервалов предсказания (prediction interval)

Посмотрим “поближе” на прогноз, который сгенерировала модель ARMA(2,1).

fcst <-  forecast(fit.best, h = 20)
plot(fcst$mean)

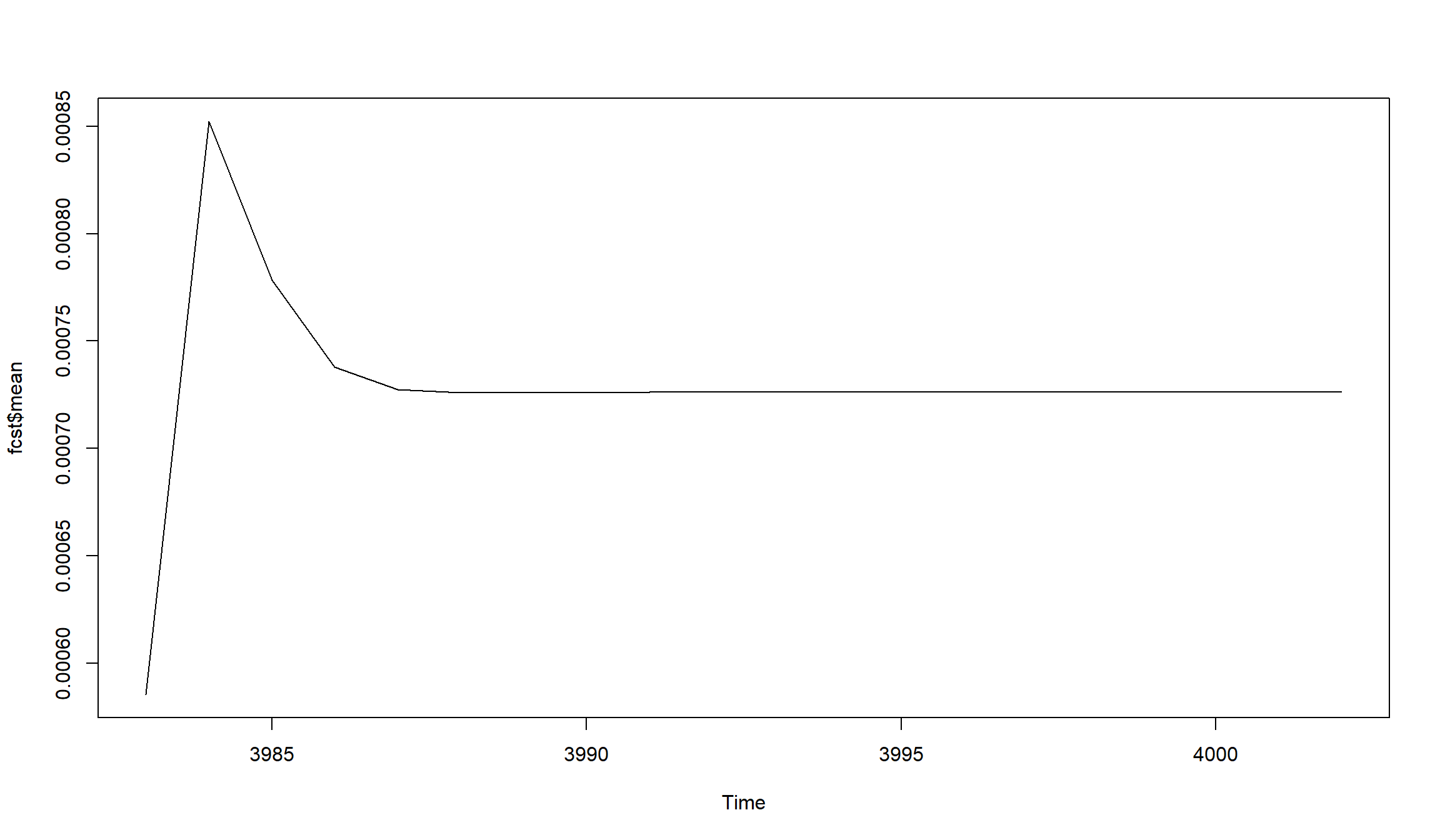
Построение прогноза с помощью auto.arima

• Пакет forecast позволяет автоматически находить лучшие спецификации ARMA моделей

fit1 <- auto.arima(diff.log.MICEX, ic = 'aicc')
fit1

Series: diff.log.MICEX 
ARIMA(4,0,0) with non-zero mean 

Coefficients:
         ar1      ar2      ar3     ar4   mean
      0.0250  -0.0402  -0.0325  0.0285  7e-04
s.e.  0.0159   0.0159   0.0159  0.0159  3e-04

sigma^2 estimated as 0.0004217:  log likelihood=9818.88
AIC=-19625.75   AICc=-19625.73   BIC=-19588.01

fcst <- forecast(fit1, h=100, level=95, fan = TRUE)
plot(forecast(fit1, h=100, level=95, fan = TRUE), col=2)

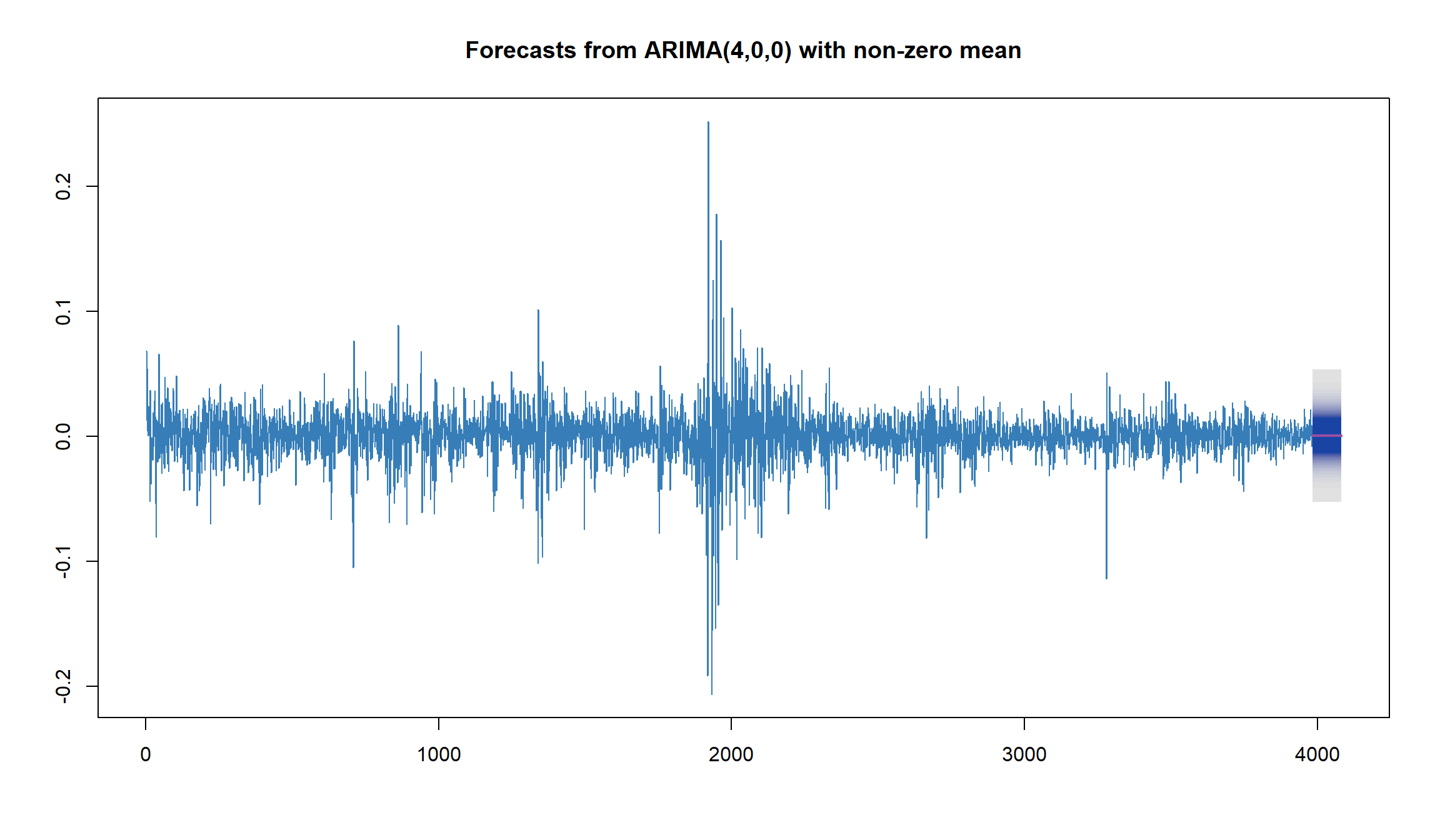
plot(fcst$mean[1:50], type  = 'l')

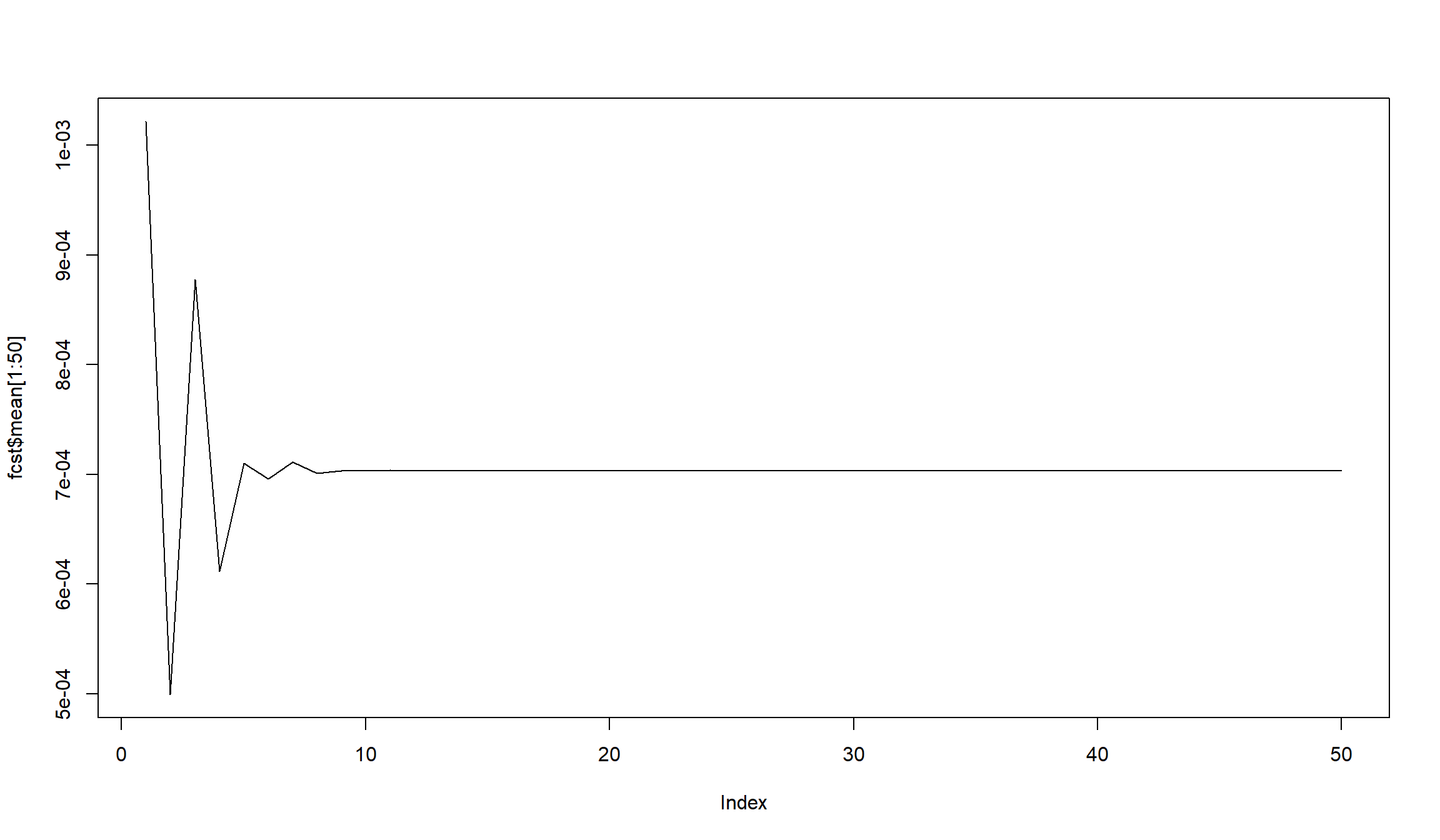
• Мы “нашли” вручную модель ARMA(2,1) или ARMA(2,0), в то время как ’auto.arima` предлагает нам модель ARMA(4,0).

ARIMA-модели

• Серия \({x_t}\) является \(ARIMA(p,d,q)\) моделью, если \(\Delta^d x_t\) является моделью \(ARMA(p,q)\).
• К примеру, если лог-доходности моделируются ARMA(p,q), то лог-цены будут ARIMA(p,1,q).
• Random walk является моделью ARIMA(0,1,0), а белый шум – моделью ARIMA(0,0,0).

мы также можем находить модели и строить прогнозы для нестационарных серий c помощью auto.arima

fit2 <- auto.arima(log.MICEX, ic = 'aicc')
fit2

Series: log.MICEX 
ARIMA(3,1,3) with drift         

Coefficients:
          ar1     ar2     ar3     ma1      ma2      ma3  drift
      -0.2862  -0.029  0.6264  0.3127  -0.0027  -0.6603  7e-04
s.e.   0.1683   0.167  0.1472  0.1614   0.1644   0.1406  3e-04

sigma^2 estimated as 0.0004212:  log likelihood=9823.16
AIC=-19630.31   AICc=-19630.28   BIC=-19580

plot(forecast(fit2, h=100, level=95, fan = TRUE), col=2)

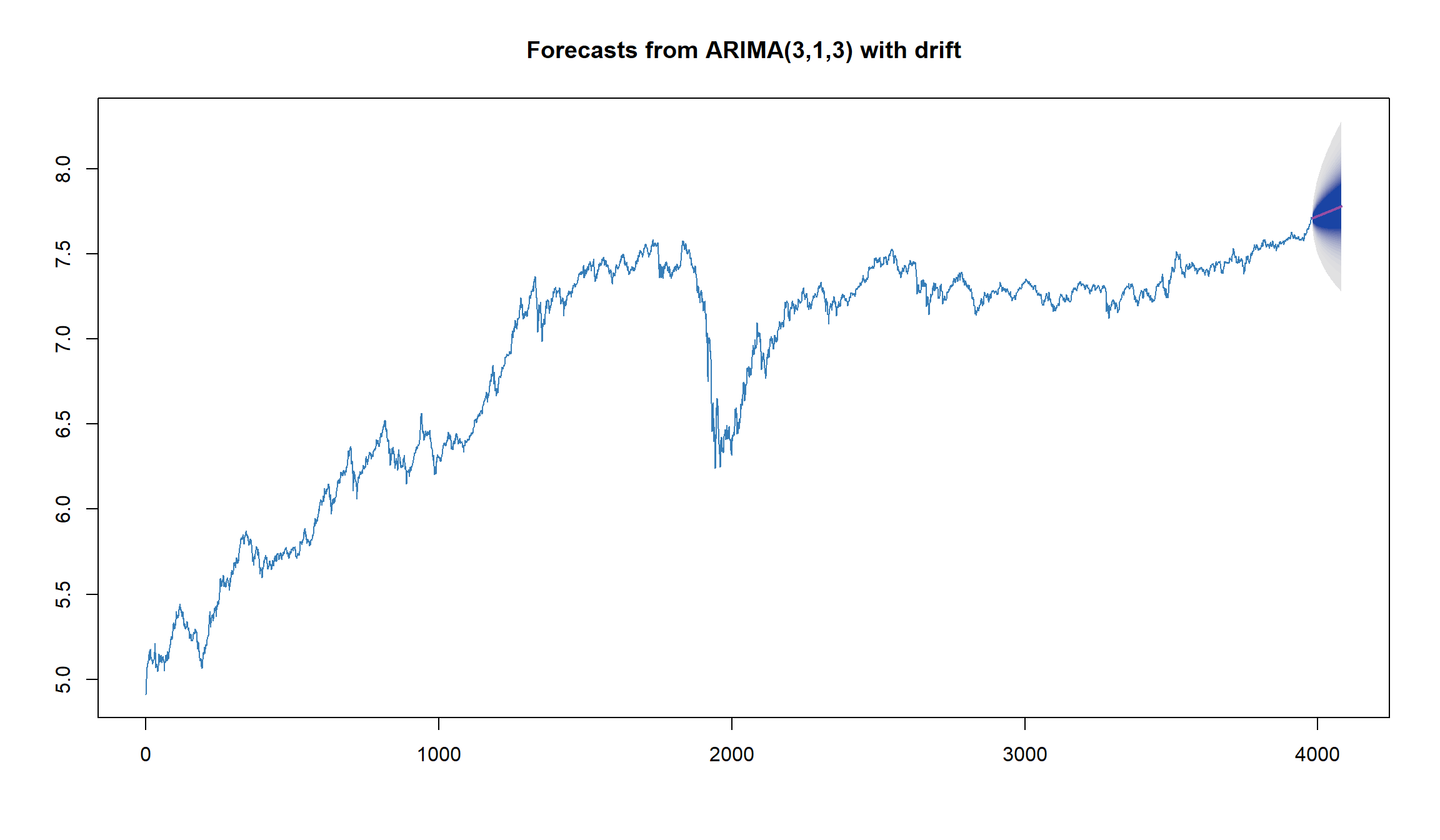
fit2 <- auto.arima(log.MICEX, ic = 'aicc', allowdrift = FALSE,allowmean = TRUE, lambda=NULL)
plot(forecast(fit2, h=100, level=95, fan = TRUE), col=2)

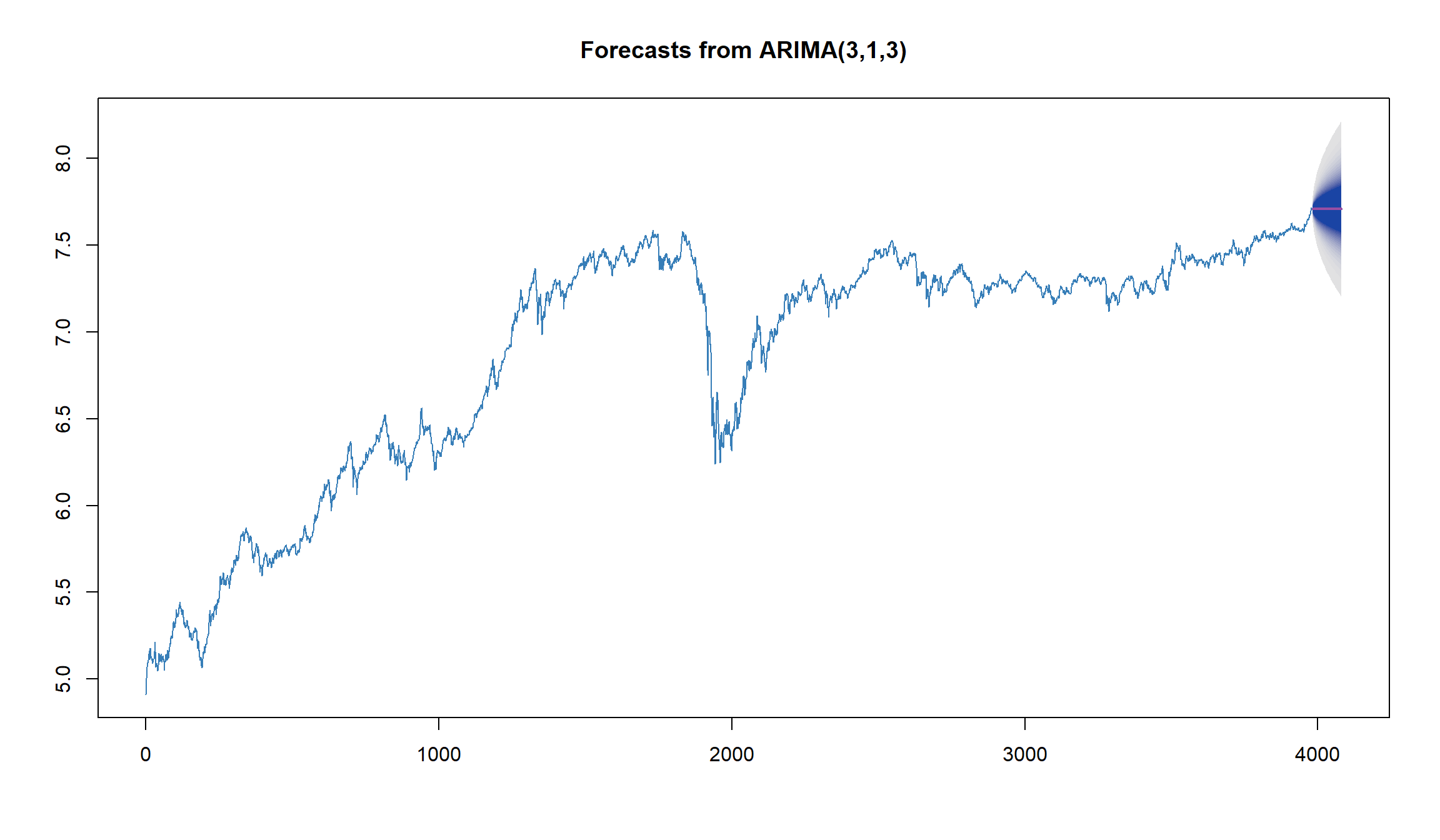
Выводы

• Мы используем PACF для определения ориентировочного порядка AR-моделей (последний значимый лаг на PACF определяет порядок модели - \(p\))
• Мы используем ACF для определения порядка MA-моделей (последний значимый лаг на АСА определяет порядок модели - \(q\)).
• Информационные критерии (AIC, BIC) часто используются для выбора оптимальной модели. Эти критерии “штрафуют” модели за сложность (количество оцениваемых параметров)
• ARMA модели позволяют использовать меньше параметров чем AR или MA по отдельности
• Все ARMA модели не позволяют моделировать меняющуюся во времени волатильность
• Прогнозы на основе ARMA имеет смысл строить только на несколько периодов вперед

Использованные источники:

1. “An Introduction to Analysis of Financial Data with R” (Ruey S. Tsay)
2. “Statistics and Data Analysis for Financial Engineering” (David Ruppert & David Matteson)
3. Analyzing Financial Data and Implementing Financial Models Using R (Clifford Ang)
4. Forecasting Financial Time Series (Patrick Perry)
5. Autoregressive Moving Average ARMA(p, q) Models for Time Series Analysis (Michael Halls-Moore)