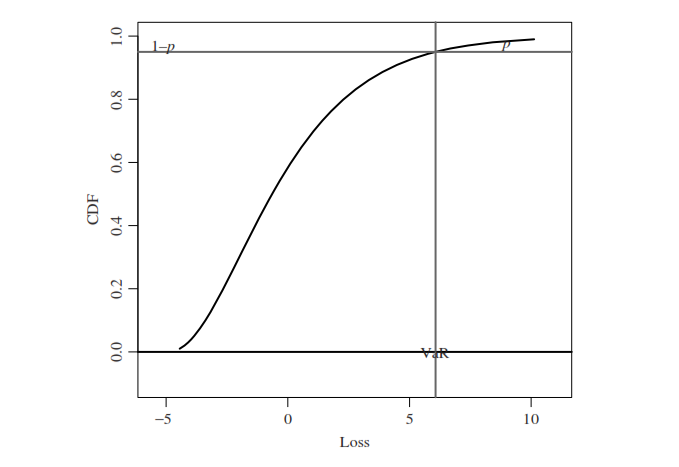
Value-at-Risk (Var) на основе функции распределения (CDF)
на данном графике p это \(\alpha\).
Салихов Марсель (marcel.salikhov@gmail.com)
2017-02-27
Есть много типов финансового риска:
Оценка риска является обязательной частью процесса принятия финансовых решений.
Сегодня мы сосредоточимся на оценке рыночного риска (market risk), но эти подходы могут (и используются) для оценки кредитного риска.
\[ X = 1000 \times (Y - 100) \] где \(Y\) – цена акции завтра. Горизонт оценки – 1 рабочий день.
Если \(L\) – убыток в течение горизонта \(T\), то \(VaR(\alpha)\) – это верхняя квантиль функции распределения \(L\). Для непрерывно функции распределения \(Var(\alpha)\) решает следующее уравнение:
\[ P\{L> VaR(\alpha)\} = \alpha \]
на данном графике p это \(\alpha\).

\[ ES(\alpha) = \frac{\int_0^{\alpha} VaR(u)du}{\alpha} \]
Предположим, что ожидаемая доходность акции составляет 0,04 и среднеквадратичное отклонение равно 0,18.
Если вы купили акций этой компании на 100 тыс. рублей, какой будет VaR при горизонте в 1 год?
Предположим, что функция распределения убытка распределена нормально с ожидаемым значением -4 тыс. рублей и СКО равным 18 тыс. рублей.
Тогда VaR будет равен:
\[-4000 + 18 000 z_{\alpha} \] где \(z_{\alpha}\) – верхняя \(\alpha\)-квантиль распределения нормального распределения.
r = 0.04
sig = 0.18
P = 100000
P*r[1] 4000P*sig[1] 18000alpha = seq(.0025,.25,by=.002)
var = -P*r + P*sig*qnorm(1-alpha)plot(alpha,var,type="l",xlab=expression(alpha),
ylab=expression(paste("VaR(",alpha,")")))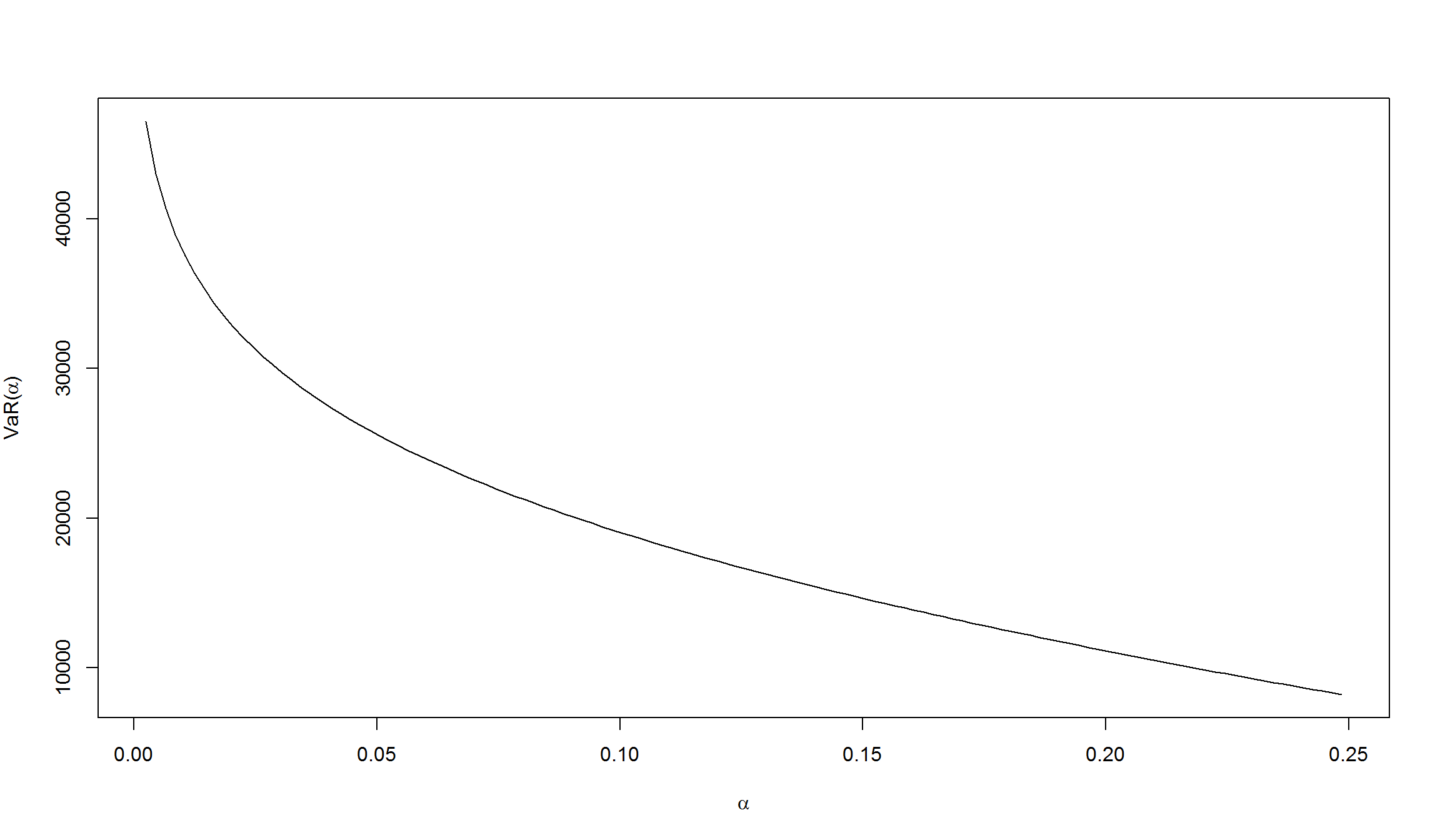
min(var);max(var)[1] 8225.917[1] 46526.61Предположим, что ваша позиция это 1 млн рублей, вложенный в индексный фонд ММВБ.
Вы хотите оценить VaR на 1 день.
Построим график ежедневных доходностей индекса ММВБ в 2010-2017 гг.
plot(MICEX.rtn, main = 'Дневные доходности индекса ММВБ')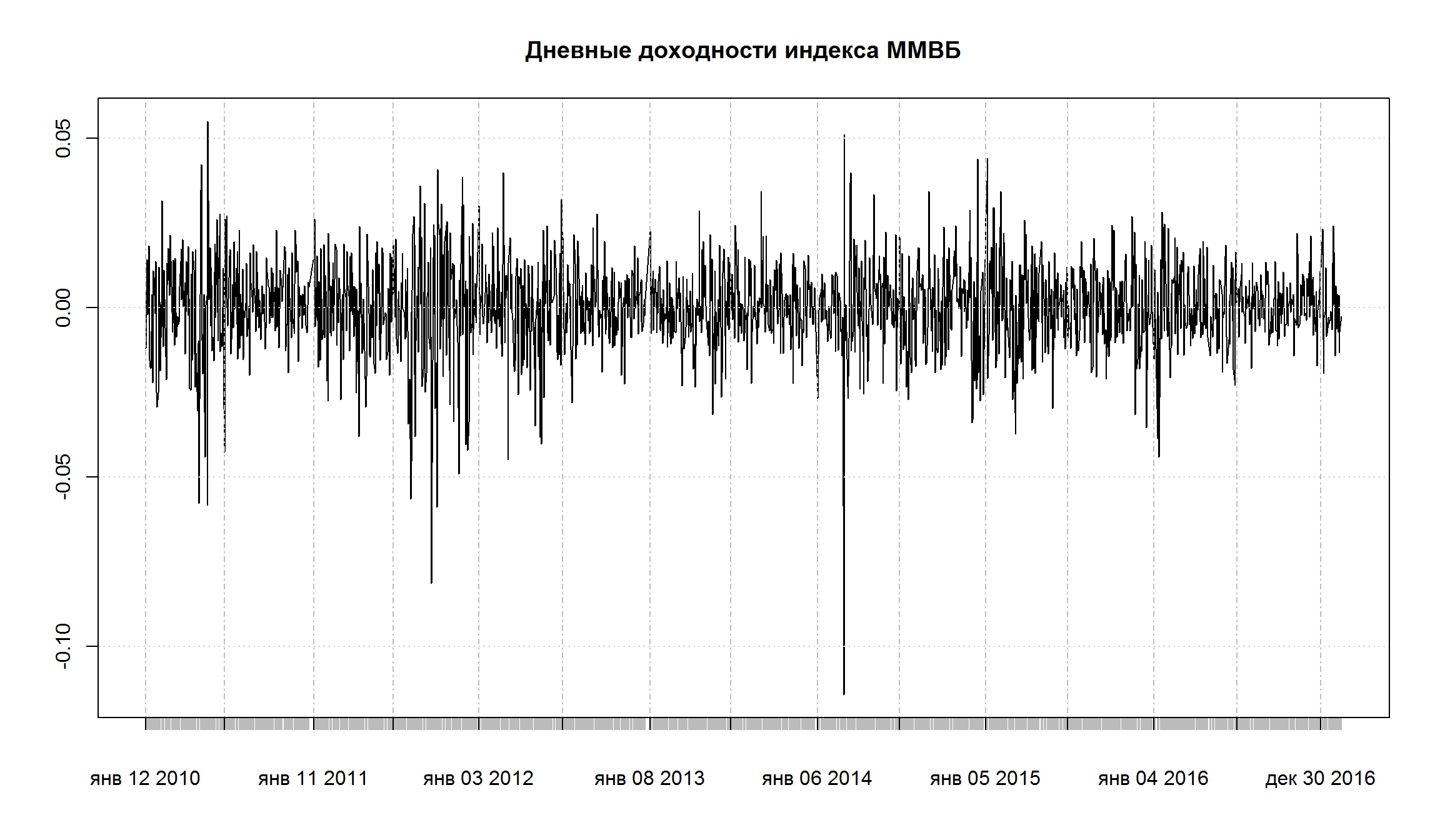
alpha = 0.05 # доверительный интервал
q <- as.numeric(quantile(MICEX.rtn, alpha))
q[1] -0.02036615Var_nonp <- -10^6 * q # непараметрический VaR
IEVar = MICEX.rtn < q # вектор логических переменных, равен TRUE, если величина доходности меньше квантили
ES_nonp = -10^6 * sum(MICEX.rtn * IEVar) / sum(IEVar) # суммируем и считаем среднее значение убытка
ES_nonp # непараметрическая оценка ES[1] 31348.335%-ая квантиль данного распределения доходностей равна 2%.
Это означает, что на исторических данных дневная доходность, превышающая 2%, наблюдалась в менее чем 5% времени.
Таким образом, мы можем оценить, что существует 5% вероятность, что убыток такого размера может возникнуть на следующий день.
\[\hat{VaR}(0,05, 1д) = 10^6 * 0,02 = 20366.15 \] ES рассчитывается путем усреднения всех доходностей, которые были меньше 2% и умножения их на величину портфеля. В нашем случае \(ES(0,05) = 31348.33\)
Параметрическая оценка дает несколько преимуществ по сравнению с непараметрической оценкой:
Пусть \(F(y|\theta)\) – параметрическое семейство распределений, используемое для моделирования доходностей.
\(\hat{\theta}\) оценка \(\theta\), оцененная, к примеру, методом максимального правдоподобия на основе исторических данных.
Тогда \(F^{-1}(\alpha|\hat{\theta})\) представляет собой оценку \(\alpha\)-квантили распределения доходностей на основе обратной эмпирической функции распределения.
VaR будет определяться как:
\[\hat{VaR}^{par}(\alpha) = -S \times F^{-1}(\alpha|\hat{\theta}) \] \(S\) – текущая величина нашей позиции.
Оценка ES будет рассчитываться как:
\[\hat{ES}^{par} = - \frac{S}{\alpha} \times \int_{-1}^{F^{-1}(\alpha|\hat{\theta})}x f(x| \hat{\theta}) dx\] В общем случае рассчитать этот интеграл может быть сложно, но для случаев нормального распределения и распределения Стьюдента существуют удобные аналитические формулы для расчета.
x = seq(-4,4, by=0.01)
plot(x, dt(x, df=10), type = 'l', main='Распределение Стьюдента с разными df и нормальное распределение')
lines(x,dt(x,df = 5), col = 'red')
lines(x,dt(x,df = 1), col = 'blue')
lines(x,dnorm(x), col = 'green', lwd = 2)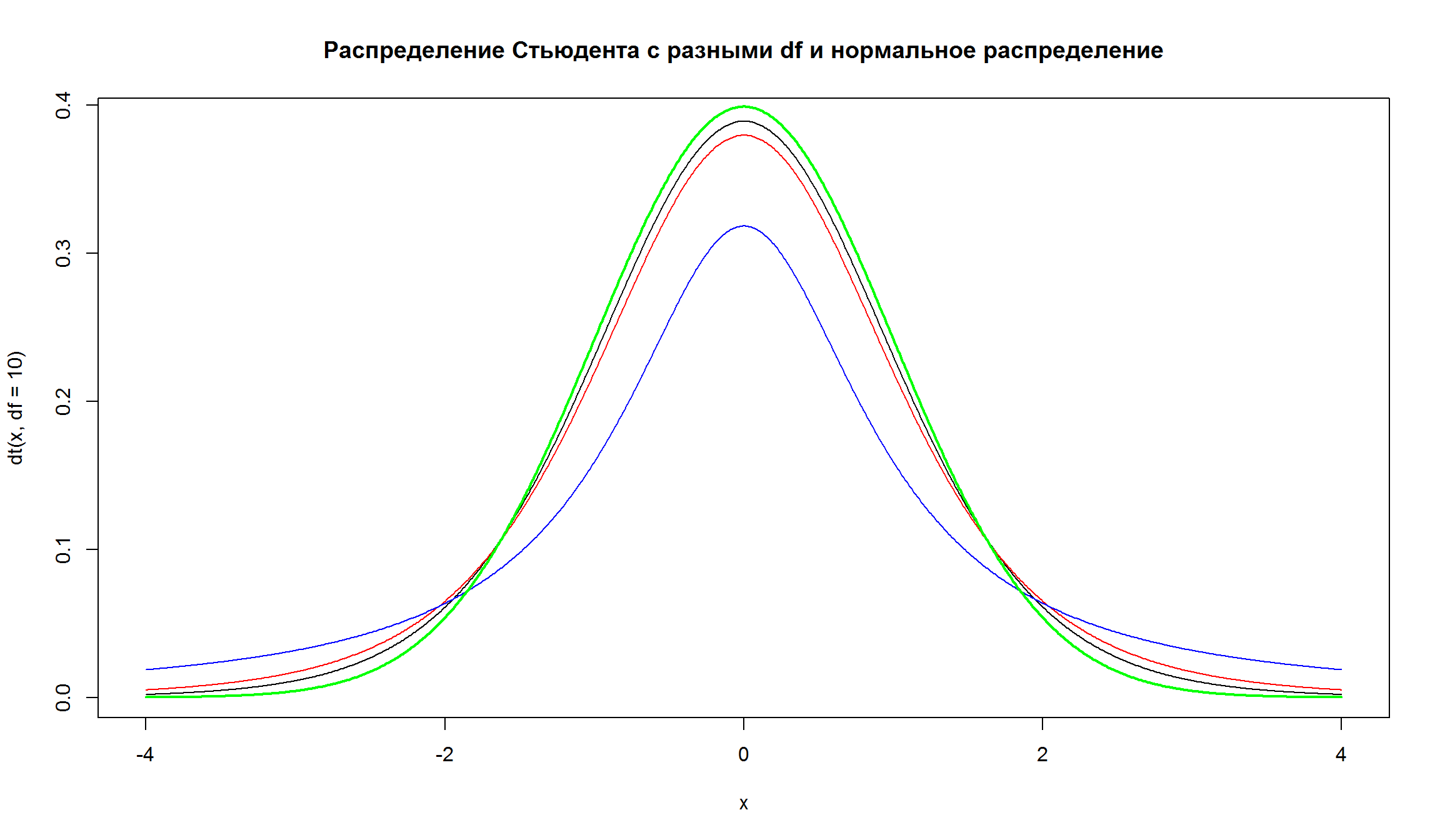
\[X = \mu + \sigma T \] или \(T = \frac{X- \mu}{\sigma}\) – имеет классическое t-распределение.
Таким образом, не-стандартизированное t-распределение Стьюдента имеет три параметра – \(\nu, \mu, \sigma\). В данном случае \(\sigma\) не является среднеквадратическим отклонением, а параметром масштаба распределения (scale parameter)
Другие характеритсика не-стандартизированного распределения Стьдента:
\[ E(x) = \mu \] \[ Var(x) = \sigma^2 \frac{\nu}{\nu-2}\]
Посчитаем параметрические оценку VaR и ES в R, предположив, что доходность индекса имеет не-стандартизированное распределение Стьюдента (i.i.d.). В рамках этого допущения VaR будет определяться как:
\[\hat{VaR}^t = -S \times \{ \hat{\mu} + q_{\alpha,t} (\hat{\mu}) \hat{\sigma} \} \] где \(\hat{\mu}, \hat{\sigma}, \hat{\mu}\) – выборочные значения среднего, коэффициента масштаба (scale parameter), индекса степенй свободы (tail index), соответственно.
\(q_{\alpha,t} (\hat{\mu})\) – \(\alpha\)-квантиль распределения Стьюдента с заданным параметром \(\mu\).
В нашем случае для доходностей индекса ММВБ:
\[ \hat{\mu} = 0.0004702794, \hat{\sigma} = 0.0101840885, \hat{\nu} = 5.16 \]
n = nrow(MICEX.rtn)
alpha = 0.05
library(MASS)
fitt <- fitdistr(MICEX.rtn,"t") # функция для оценки различных одномерых распределения с помощью MLE из пакета MASS
param <- as.numeric(fitt$estimate)
mean <- param[1]
df <- param[3]
sd <- param[2]*sqrt( (df)/(df-2) ) #расчет стандартного отклонения через scale и df по формуле
sigma <- param[2]
qalpha <- qt(alpha,df=df) # квантиль-функция для распределения Стьюдента (t)
VaR_par <- -10^6 *(mean + sigma*qalpha)
es1 <- dt(qalpha,df=df)/(alpha)
es2 <- (df + qalpha^2) / (df - 1)
es3 = -mean+sigma*es1*es2
ES_par <- 10^6 *es3
VaR_par[1] 19905.36ES_par[1] 28591.27Параметрическая оценка VaR (19905) близка к непараметрической оценке (20366), но несколько меньшее ее. Параметрическая оценка ES = 28591, что меньше чем не-параметрическая оценка ES (31348). Это связано с тем, что наиболее левая часть распределения доходностей (90 из 1782 наблюдений) является более тяжелой по сравнению с распределением Стьюдента с df = 5.16
Формула ES для распределения Стьюдента, используемая в расчете:
\[\hat{ES}^t = S \times \{ -\mu + \sigma \frac{f_{_\nu}F_{\nu}^{-1}(\alpha)}{\alpha}[\frac{\nu+\{F_{\nu}^{-1}(\alpha)\}^2\}}{\nu-1}] \} \]
Красная линия – график квантилей распределения Стьюдента с зафиксированным значением df = 5.16
Точки - точки наблюдений исторической доходности.
В левой нижней части графика красная линия находится ниже точек. Это означает, что распределение Стьюдента имеет менее тяжелый хвост по сравнению с эмпирическими наблюдениями.
grid = (1:n)/(n+1)
qqplot(coredata(MICEX.rtn), qt(grid,df=5.16),main="Распределение Стьдента,df=5.16",xlab="данные",ylab="t-квантили")
abline(lm(qt(c(.25,.75),df=5.16)~quantile(MICEX.rtn,c(.25,.75))), col = 'red', lwd = 2)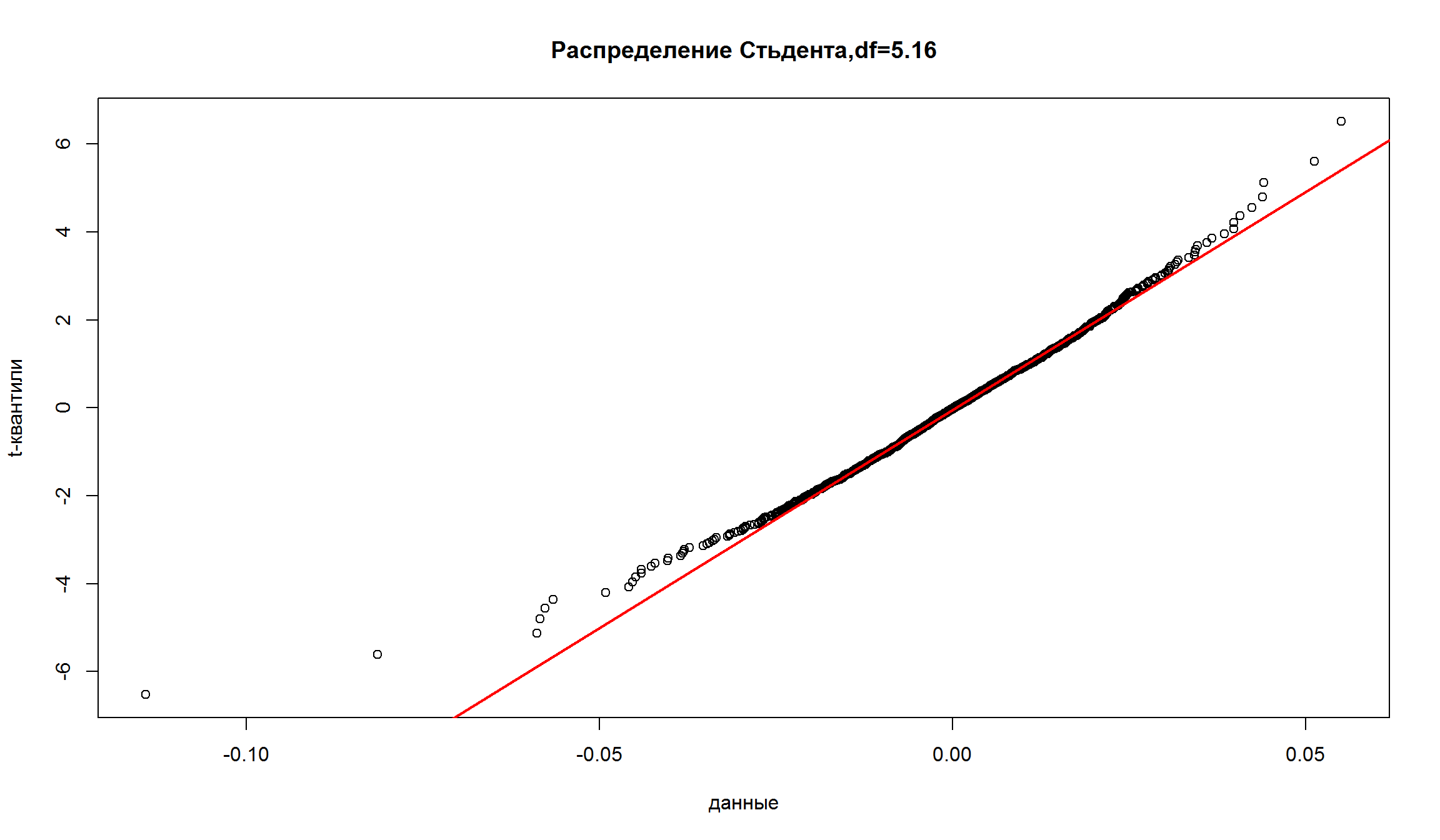
Оценка VaR и ES – это только оценки. Если мы будем использовать другие временные периоды мы будем получать другие оценки риска. Мы посчитали точность VaR до второго знака после запятой, однако на сколько мы на самом деле можем быть уверены в этих оценках?
Для оценки доверительных интервалов VaR и ES мы можем использовать метод бутстрапа.
В бутстрапе мы из имеющейся выборки случайным образом формируем под-выборку с репликацией (то есть одни и теж же значения имеют шансы попасть в под-выборку несколько раз) и оцениваем параметры.
Мы будем создавать выборки с репликацией из нашего ряда доходностей (размера 1000) и проводить ту же самую процедуру – непараметрическую оценку и параметрическую оценку VaR и ES и сохранять полученные значения.
Выполнение кода занимает около 5 минут даже на современном производительном компьютере – бустрап оценки имеют “вычислительную” цену.
B = 1000 # количество выборок
VaRs=matrix(0,nrow=B,ncol=4) # матрица для хранения значений риск-метрик
alpha = 0.05
set.seed(1234)
for (i in (1:B))
{
returns_b = sample(MICEX.rtn,1000,replace=TRUE) # бутстрап-выборка
q_b = as.numeric(quantile(returns_b,.05))
VaR_nonp_b = -10^6*q_b
IEVaR_b = (returns_b < q_b)
ES_nonp_b = -10^6 * sum(returns_b*IEVaR_b) / sum(IEVaR_b)
fitt_b = fitdistr(returns_b,"t")
param_b = as.numeric(fitt_b$estimate)
mean_b = param_b[1]
df_b = param_b[3]
sd_b = param_b[2]*sqrt( (df_b)/(df_b-2) )
lambda_b = param_b[2]
qalpha_b = qt(.05,df=df_b)
VaR_par_b = -10^6*(mean_b + lambda_b*qalpha_b)
es1_b = dt(qalpha_b,df=df_b)/(alpha)
es2_b = (df_b + qalpha_b^2) / (df_b - 1)
es3_b = -mean_b+lambda_b*es1_b*es2_b
ES_par_b = 10^6*es3_b
VaRs[i,]=c(VaR_nonp_b,VaR_par_b,ES_nonp_b,ES_par_b)
cat('итерация', i)
}Посмотрим на распределение полученных оценок риска:
hist(VaRs[,1], breaks = 50, main = 'Непараметрическая оценка VaR (бутстрап)', xlab= 'рублей')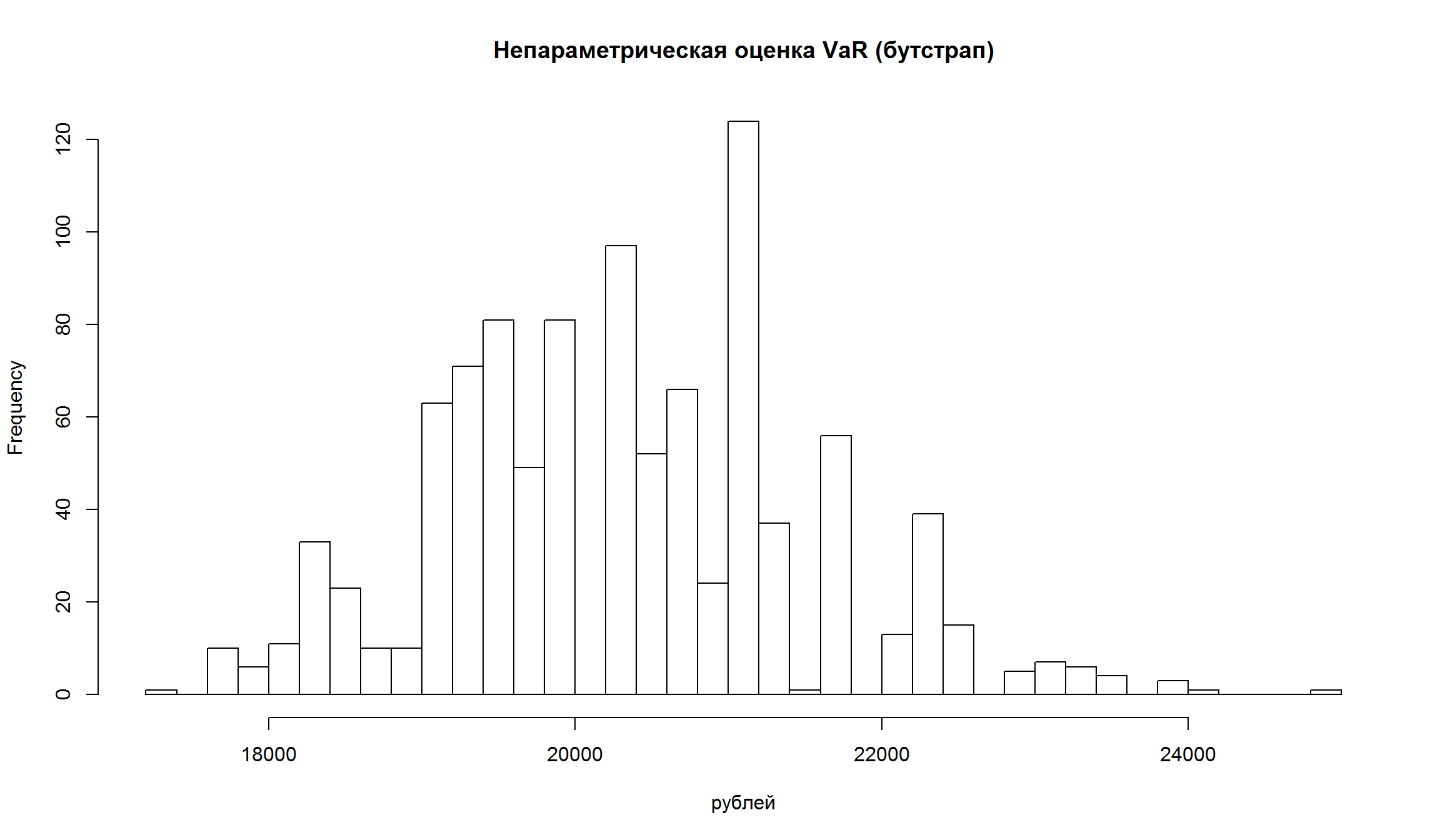
hist(VaRs[,2], breaks = 50, main = 'Параметрическая оценка VaR (бутстрап)', xlab= 'рублей')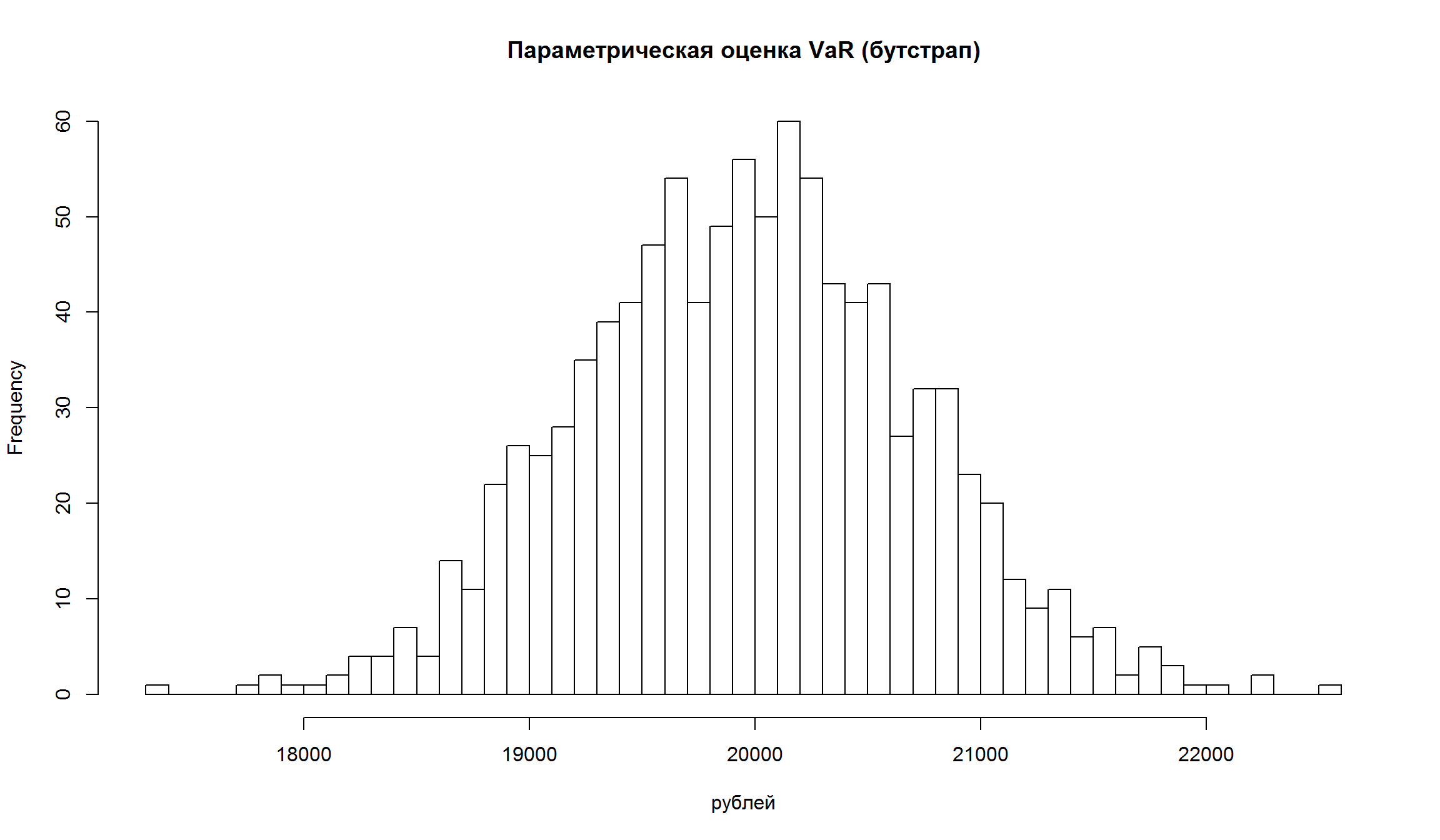
hist(VaRs[,3], breaks = 50, main = 'Непараметрическая оценка ES (бутстрап)', xlab= 'рублей')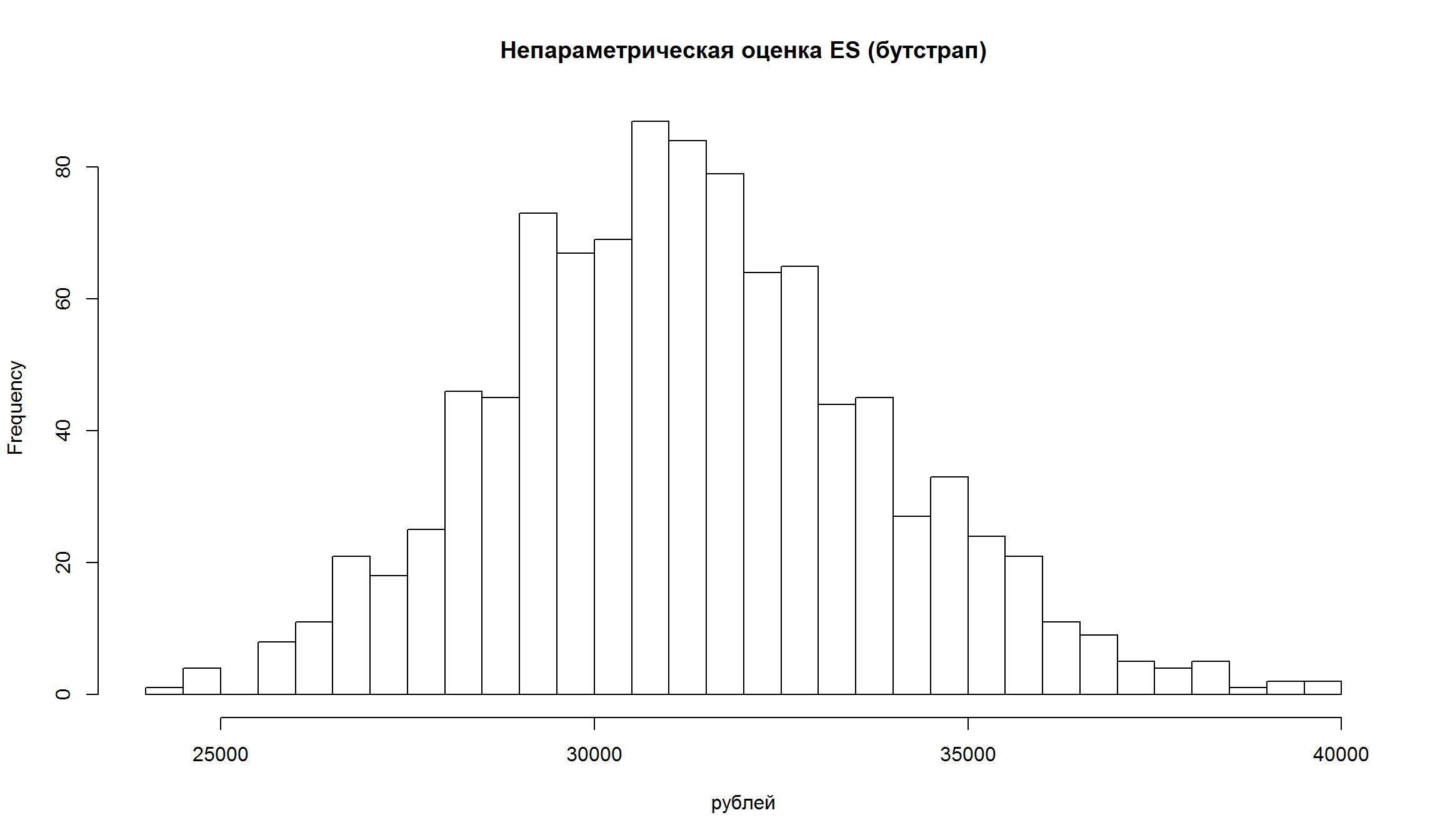
hist(VaRs[,4], breaks = 50, main = 'Параметрическая оценка ES (бутстрап)', xlab= 'рублей')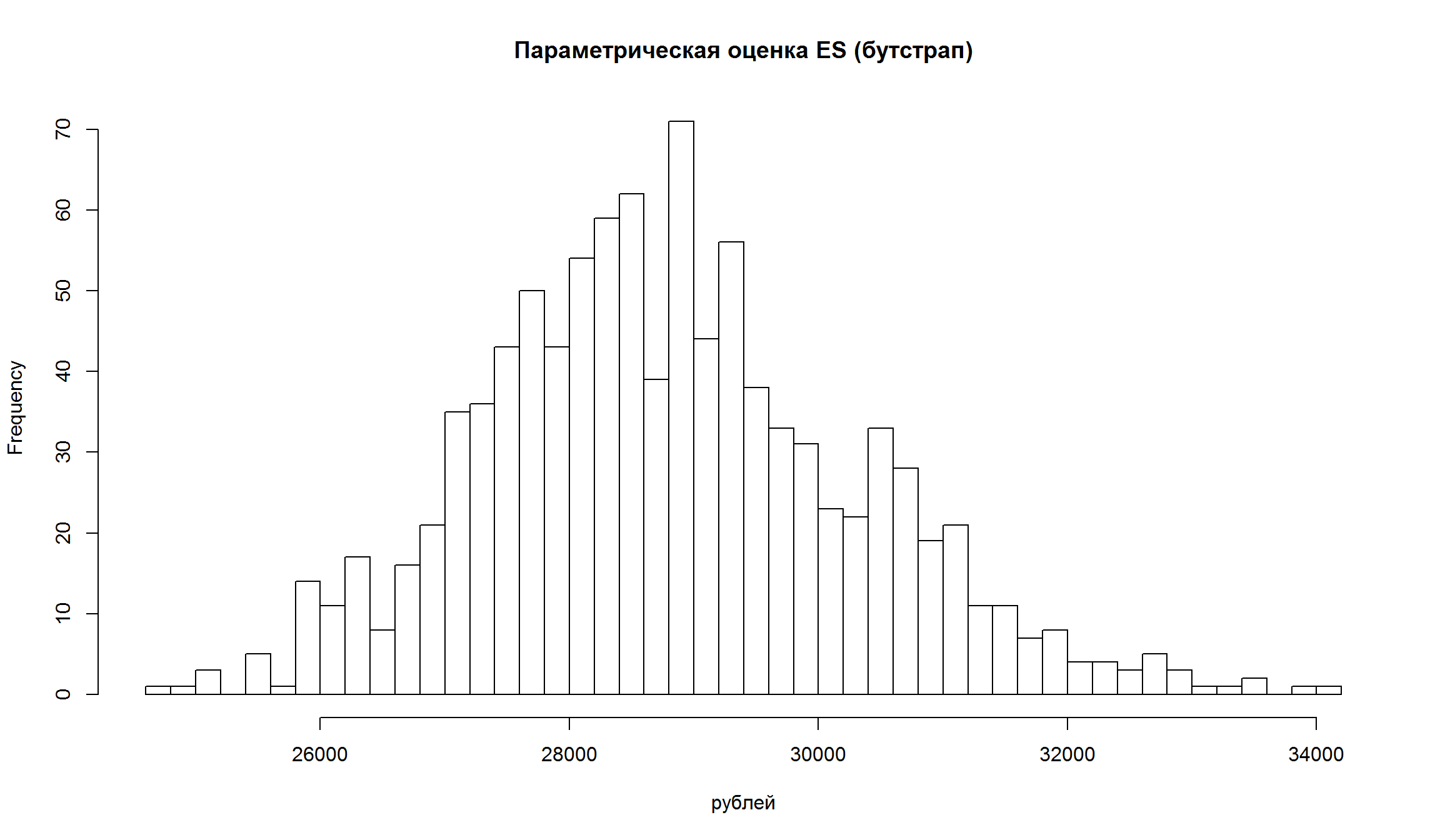
Можно использовать модель ARMA+GARCH,которые мы изучали ранее для оценки риск-метрик.
Оценким GARCH(1,1) для доходностей индекса ММВБ с помощью пакета rugarch.
library(fGarch)
library(rugarch)
garch.t = ugarchspec(mean.model=list(armaOrder=c(0,0)),
variance.model=list(garchOrder=c(1,1)),
distribution.model = "std")
micex.garch <- ugarchfit(data=MICEX.rtn, spec=garch.t)
micex.garch
*---------------------------------*
* GARCH Model Fit *
*---------------------------------*
Conditional Variance Dynamics
-----------------------------------
GARCH Model : sGARCH(1,1)
Mean Model : ARFIMA(0,0,0)
Distribution : std
Optimal Parameters
------------------------------------
Estimate Std. Error t value Pr(>|t|)
mu 0.000516 0.000256 2.0188 0.043506
omega 0.000003 0.000002 1.4295 0.152861
alpha1 0.060380 0.014335 4.2120 0.000025
beta1 0.920446 0.017775 51.7833 0.000000
shape 7.279847 1.089357 6.6827 0.000000
Robust Standard Errors:
Estimate Std. Error t value Pr(>|t|)
mu 0.000516 0.000233 2.21365 0.026853
omega 0.000003 0.000007 0.44907 0.653378
alpha1 0.060380 0.032801 1.84082 0.065648
beta1 0.920446 0.047432 19.40551 0.000000
shape 7.279847 1.678605 4.33684 0.000014
LogLikelihood : 5358.613
Information Criteria
------------------------------------
Akaike -6.0085
Bayes -5.9932
Shibata -6.0086
Hannan-Quinn -6.0029
Weighted Ljung-Box Test on Standardized Residuals
------------------------------------
statistic p-value
Lag[1] 2.812 0.09358
Lag[2*(p+q)+(p+q)-1][2] 3.322 0.11482
Lag[4*(p+q)+(p+q)-1][5] 4.494 0.19857
d.o.f=0
H0 : No serial correlation
Weighted Ljung-Box Test on Standardized Squared Residuals
------------------------------------
statistic p-value
Lag[1] 0.0798 0.7776
Lag[2*(p+q)+(p+q)-1][5] 0.2106 0.9918
Lag[4*(p+q)+(p+q)-1][9] 0.4272 0.9991
d.o.f=2
Weighted ARCH LM Tests
------------------------------------
Statistic Shape Scale P-Value
ARCH Lag[3] 0.02757 0.500 2.000 0.8681
ARCH Lag[5] 0.12848 1.440 1.667 0.9813
ARCH Lag[7] 0.29790 2.315 1.543 0.9929
Nyblom stability test
------------------------------------
Joint Statistic: 19.9586
Individual Statistics:
mu 0.06951
omega 1.50818
alpha1 0.24984
beta1 0.18004
shape 0.13645
Asymptotic Critical Values (10% 5% 1%)
Joint Statistic: 1.28 1.47 1.88
Individual Statistic: 0.35 0.47 0.75
Sign Bias Test
------------------------------------
t-value prob sig
Sign Bias 0.5897 0.5555
Negative Sign Bias 0.1715 0.8639
Positive Sign Bias 0.7351 0.4624
Joint Effect 2.4900 0.4771
Adjusted Pearson Goodness-of-Fit Test:
------------------------------------
group statistic p-value(g-1)
1 20 15.10 0.7159
2 30 29.01 0.4645
3 40 37.17 0.5536
4 50 50.15 0.4274
Elapsed time : 0.480839 plot(micex.garch, which = 2) # пакет rugarch рисует график с 1% VaR
please wait...calculating quantiles...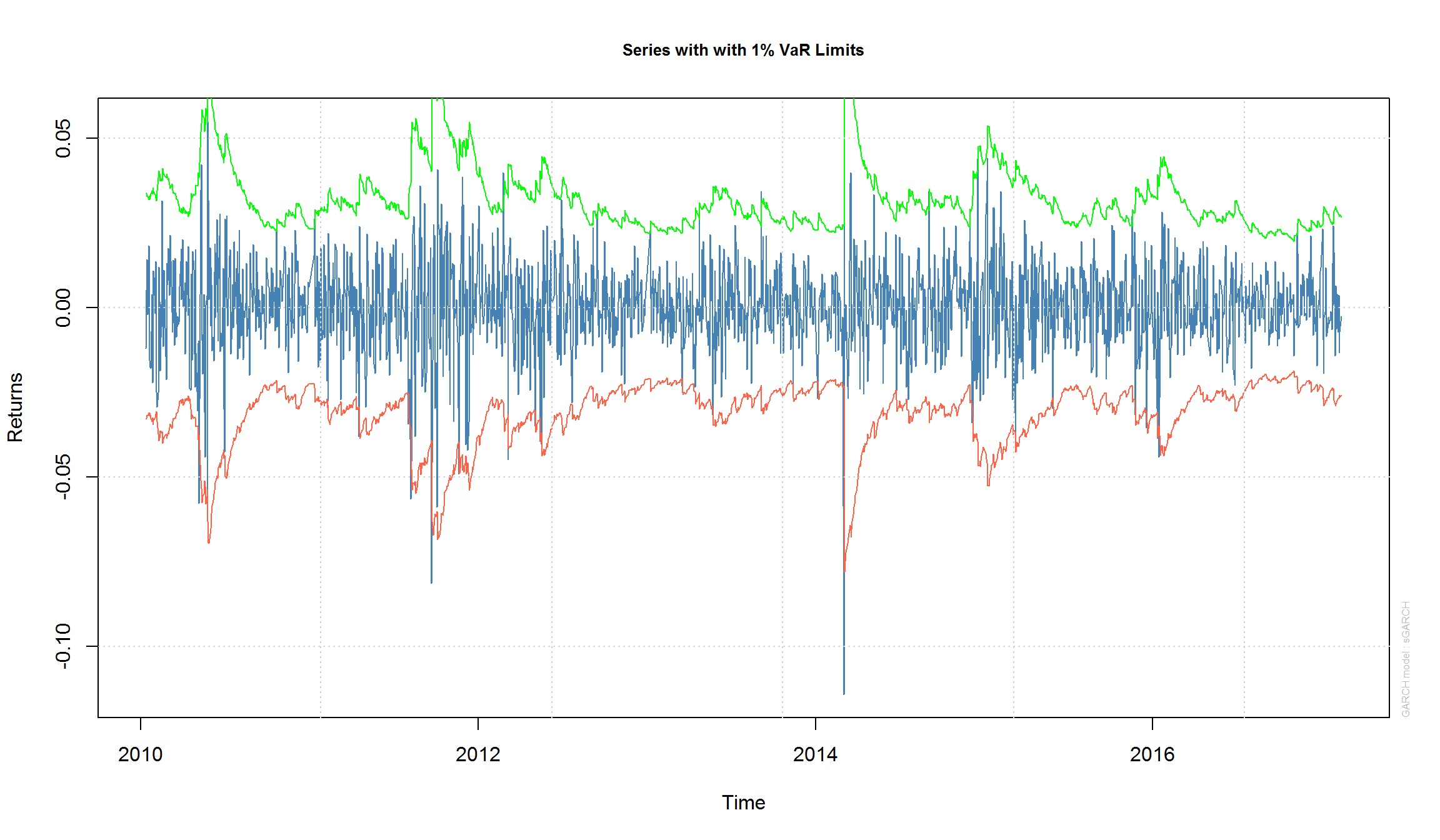
pred <- ugarchforecast(micex.garch, data = MICEX.rtn, n.ahead = 1) # получить прогноз на следующий день
pred
*------------------------------------*
* GARCH Model Forecast *
*------------------------------------*
Model: sGARCH
Horizon: 1
Roll Steps: 0
Out of Sample: 0
0-roll forecast [T0=2017-02-13]:
Series Sigma
T+1 0.0005162 0.01019nu <- as.numeric(coef(micex.garch)[5]) # shape paramter
q <- qstd(alpha, # функция квантили распределения Стьюдента из пакета fGarch
mean <- fitted(pred),
sd <- sigma(pred),
nu <- nu )
VaR <- -10^6*q ; VaR 2017-02-13
T+1 15827.6lambda <- sigma(pred)/sqrt( (nu)/(nu-2) )
qalpha <- qt(alpha, df<-nu)
es1 <- dt(qalpha, df=nu)/(alpha)
es2 <- (nu + qalpha^2) / (nu - 1)
es3 <- -mean+lambda*es1*es2
ES_par <- 10^6*es3 ; ES_par 2017-02-13
T+1 21777.13Пакет PerformanceAnalytics имеет функции для расчета VaR и ES.
require(PerformanceAnalytics)
VaR(MICEX.rtn, method="historical", p = 0.95) MICEX.Close
VaR -0.02036615VaR(MICEX.rtn, method="gaussian", p = 0.95) MICEX.Close
VaR -0.02146554ES(MICEX.rtn, method="historical", p = 0.95)*10^6 MICEX.Close
ES -31348.33ES(MICEX.rtn, method="gaussian", p = 0.95)*10^6 MICEX.Close
ES -26975.78Пакет не позволяет использовать распределение Стьюдента для доходностей, но зато есть другие методы.
Мы можем использовать подходы из портфельного анализа, чтобы оценить среднее и дисперсию портфеля бумаг для того, чтобы оценить VaR и ES.
require(mvtnorm)
require(mnormt)
require(rgl)
rtns2 <- rtns[,1:2] # две бумаги - Газпром и Сбербанк
mu <- c(mean(rtns2[,1]), mean(rtns2[,2])) # вектор средних
Sigma <-cov(rtns2) # матрица ковариаций
set.seed(1234)
bivn <- mvrnorm(5000, mu = mu, Sigma = Sigma ) # cимулируем многомерное нормальное
bivn.t <- rmt(5000, mu, Sigma, df = 3.45) # симулирование данных. df нашли методом MLEЕсли мы сравним симулированные значения многомерного нормального и t-распределения, то увидим, что нормальное распределение - горадо более “сжато” относительно среднего значения.
par(mfrow=c(1,3))
plot(bivn.t[,1], bivn.t[,2], main = 'Двумерное t-распределение', xlab = 'GAZP', ylab='SBER')
plot(bivn[,1],bivn[,2],main = 'Двумерное нормальное распределение', xlab = 'GAZP', ylab='SBER',
ylim=c(-.4,0.4), xlim = c(-0.3, 0.5))
plot(coredata(rtns[,1]),coredata(rtns[,2]),main = 'Исторические данные', xlab = 'GAZP', ylab='SBER',
ylim=c(-.4,0.4), xlim = c(-0.3, 0.5))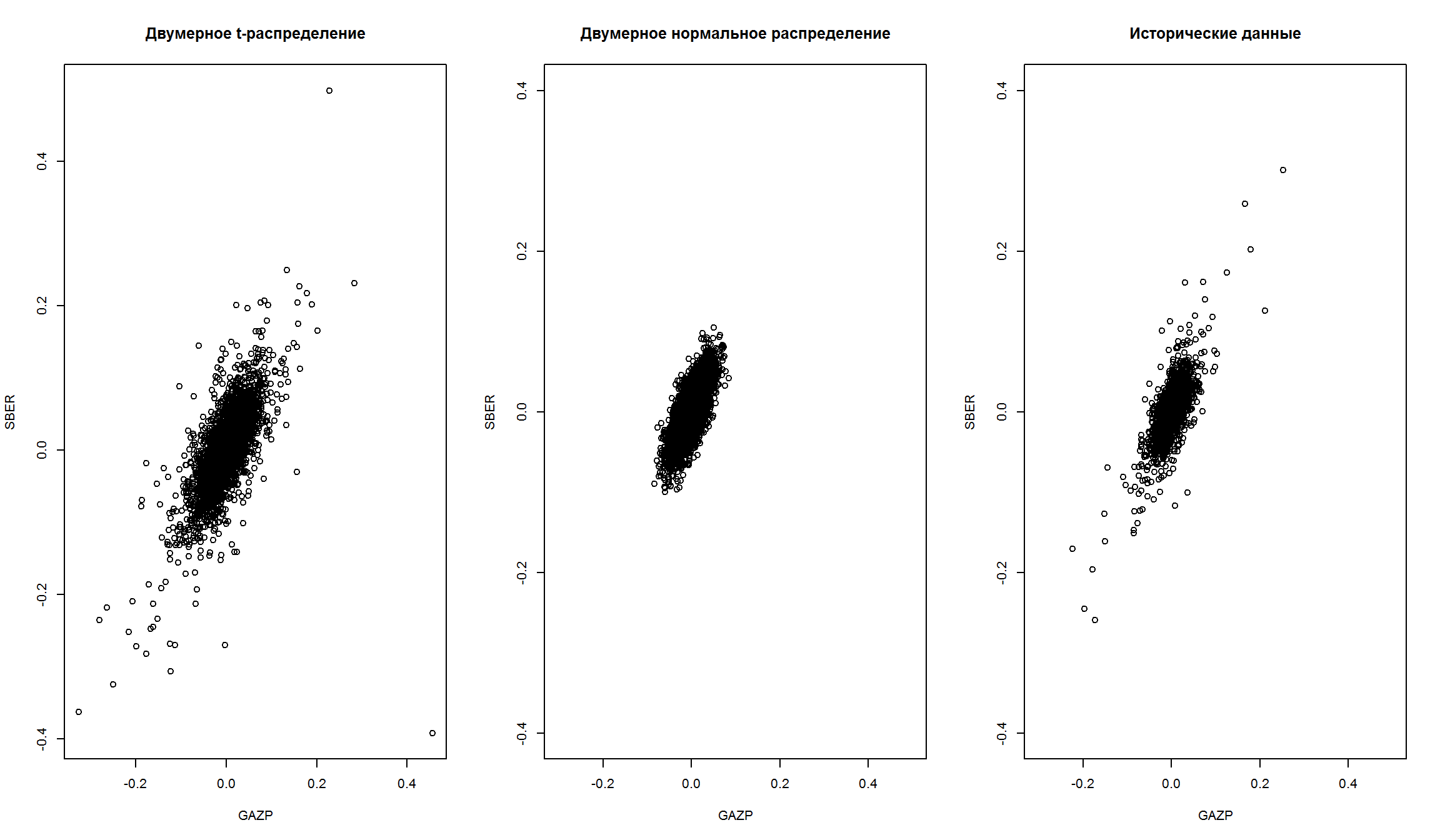
par(mfrow=c(1,1))Мы можем построить красивый трехмерный график, который показывает плотностей двумерного распределения Стьюдента с эмпирическими параметрами.
bivn.kde <- kde2d(bivn.t[,1], bivn.t[,2], n = 100) #оценка двумерного ядра (kernel) плотности распределения
col2 <- heat.colors(length(bivn.kde$z))[rank(bivn.kde$z)] # регулирование цвета
persp3d(x=bivn.kde, col = col2, xlab="GAZP", ylab = 'SBER')
rglwidget(width=800, heigh=600) +Пусть у нас есть портфель из трех акций – Газпром, Сбербанк, ГМК Норникель. + Стоимость портфеля = 1 млн рублей, распределенных равными долями. То есть доля каждой бумаги в портфеле равна 1/3 + Оценим VaR и ES для данного портфеля с допущением, что доходности бумаги имеют многомерное t-распределение.
require(mnormt)
alpha = .05
rtns3 <- rtns[,1:3]
cor(rtns3) # матрица корреляций 3 бумаг GAZP SBER GMKN
GAZP 1.0000000 0.7454712 0.6419966
SBER 0.7454712 1.0000000 0.5747359
GMKN 0.6419966 0.5747359 1.0000000df = seq(2.0,7.0,.05) # вектор возможных значений параметра тяжести хвоста (tail index)
n = length(df)
loglik = rep(0,n)
# найдем параметр df, который максимизирует log-likelehood
for(i in 1:n){
fit = cov.trob(rtns3,nu=df) # оценка матрицы ковариации для многомерного t-распределения
loglik[i] = sum(log(dmt(rtns3,mean=fit$center,S=fit$cov,df=df[i])))
}
indicate = (1:length(df))[ (loglik== max(loglik)) ]
dfhat = df[indicate] # максизирующей LL значение df
estim = cov.trob(rtns3,nu=dfhat,cor=TRUE) # оценка матрицы ковариации для многомерного t-распределения
options(digits=3)
muhat = estim$center
covhat = estim$cov
dfhat;muhat;covhat # основные параметны многомерного распределения[1] 3.4 GAZP SBER GMKN
-0.000444 0.000617 0.000476 GAZP SBER GMKN
GAZP 0.000220 0.000177 0.000144
SBER 0.000177 0.000317 0.000157
GMKN 0.000144 0.000157 0.000274w = rep(1/3,3) # равные веса в портфеле
muP = as.numeric(w %*% muhat) #ожидаемая доходность портфеля
varP = as.numeric(w %*% covhat %*% w) #дисперсия портфеля
sdP = sqrt(varP) # с.к.о. порфеля
muP[1] 0.000216sdP[1] 0.014sigmaP = sqrt((dfhat-2)/dfhat) * sdP # параметр лямбда для распределения Стьюдента
sigmaP[1] 0.00899VaR = -(muP + sigmaP* qt(alpha,dfhat))
10^6*VaR[1] 19968qalpha = qt(alpha,df=dfhat)
es1 = dt(qalpha,df=dfhat)/(alpha)
es2 = (dfhat + qalpha^2) / (dfhat - 1)
es3 = -muP+sigmaP*es1*es2
ES_par = 10^6*es3
ES_par[1] 31539