Количественные финансы. Вводная лекция

Введение в курс

• Курс по выбору. Фокус – работа с финансовыми данными/построение количественных моделей на практике.
• Основная задача – научиться работать с данными, расширить понимание эконометрических методов в применении к финансам.
• Семинарские занятия – работа с R.
• Мы будем говорить как о теории, так и о практике. Оба аспекта важны.
• Отдельный фокус – работа с российскими данными
• Форма контроля – семинарские занятия – лабораторные работы (50%), письменный экзамен – тест и задачи (50%).

Структура курса

1. Принципы финансов
2. Финансовые данные и первичный (исследовательский) количественный анализ
3. Обработка и первичный анализ финансовых данных
4. Линейные модели финансовых временных рядов
5. Модель оценки стоимости капитала (CAPM)
6. Риск и волатильность – модели VaR и Expected Shortfall (ES)
7. Портфельная теория
8. Модели процентных ставок
9. Использование симуляционных моделей для оценки неопределенности

Основная литература

“An Introduction to Analysis of Financial Data with R” (Ruey S. Tsay)

“Statistics and Data Analysis for Financial Engineering” (David Ruppert & David Matteson)

Зачем вообще изучать финансы?

• Работа в финансовой сфере – банки, инвестиционные компании, фонды и проч.
• Личные финансовые решения – всем придется с этим столкнуться. Необходимо понимать, как устроена финансовая система и учиться принимать рациональные финансовые решения.
• Финансы – это в первую очередь, работа с данными и цифрами. Эти навыки могут пригодиться и в других сферах.

Основные принципы финансов

1. Время имеет цену
2. Риск требует компенсации (доходности)
3. Информация – основа принятия решений
4. Цены определяются рынками
5. Финансовая устойчивость увеличивает благосостояние

1. Время имеет “цену”

• Время влияет на стоимость финансовых инструментов. Процентная ставка выплачивается, чтобы компенсировать кредитору время, в течение которого заемщик будет пользоваться его деньгами.
• Пример заемщика – кредит на покупку автомобиля. Пример кредитора – вклад в банке.
  
• Процентные ставки являются фундаментальным понятием в финансах и отражают временную стоимость денег.

2. Риск требует компенсации (доходности)

• Мир по определению полон неопределенности. Поэтому рациональный агент принимает на себя риски только если будет вознагражден.
• В финансах это вознаграждение осуществляется в форме непосредственных платежей: больше риск – больше платеж.
• Управление риском означает, что вы рассматриваете весь спектр возможных исходов. К примеру, вы можете отказаться от некоторых видов риска, снизить другие – заплатив кому-либо и жить с оставшимися рисками. Пример управления риском - страховка на автомобиль.
• Финансовая система помогает управлять рисками.

3. Информация – основа принятия решений

• В современном мире люди собирают информацию прежде, чем принимают решения. Чем более важно решение, тем больше информации мы собираем.
• Сбор и переработка информации для того, чтобы принять решение – основа финансовой системы.
• Пример. Каким образом банк принимает решение о выдаче кредита?

4. Цены определяются рынками

• Понятие рынка лежит в основе современной экономической системы.
• Финансовая система собирает информацию от большего количества участников, агрегирует ее в ценовые стимулы, которые определяют, что ценно, а что – нет.
• Финансовая система, определяя цены на стоимость кредита, стоимость акций и проч. – выступает основой распределения капитала в современных экономиках.
  
• Развитая и эффективная финансовая система способствует экономическому росту и росту благосостояния.

5. Устойчивость улучшает благосостояние

• Большинство из нас предпочитает стабильные доходы изменяющимся.
• Стабильность является предпочтительной характеристикой и для финансовой системы.
• Обеспечение экономической и финансовой стабильности – одна из основных задач центральных банков.
• Стабильная экономика растет быстрее, чем нестабильная – результаты исследований.

Основные части финансов

1. Деньги
2. Финансовые инструменты
3. Финансовые рынки
4. Финансовые институты
5. Регулирующие органы
6. Центральный банк (денежные власти)

Финансовые инструменты

Примеры финансовых инструментов, которые обеспечивают сохранение стоимости во времени:

1. Банковский вклад
2. Облигации – форма публичного займа.
3. Акции

Примеры инструментов, которые обеспечивают перенос риска:

1. Страховка
2. Фьючерсный контракт
3. Опцион
4. Своп

Финансовые рынки

• Финансовые рынки – это места, на которых финансовые инструменты покупаются и продаются.
• Финансовые рынки выполняют несколько основных функций :

1. обеспечивают ликвидностью участников
2. агрегируют и обеспечивают передачу информации
3. обеспечивают распределение риска

Структура финансовых рынков:

• Первичный рынок или Вторичный рынок
• Централизованная площадка (биржа) или OTC (over-the-counter)
• Долговой или Фондовый или Производных инструментов

Финансовые институты

Специализированные финансовые институты снижают транзакционные издержки функционирования финансовой системы.
Основные типы финансовых институтов:

1. Банки – принимают вклады и выдают кредиты
2. Страховые компании – принимают страховые премии в обмен на принятие рисков определенных событий (страхование имущества, страхование жизни)
3. Пенсионные фонды – обеспечивают инвестирование средств участников в ценные бумаги и другие активы.
4. Прочие участники рынка ценных бумаг (брокеры, управляющие компании, паевые инвестиционные фонды - ПИФы, хедж-фонды, фонды private equity)
5. Государственные финансовые компании (банк развития - ВЭБ, поддержка ипотечного рынка - Агентство по ипотечному жилищному кредитованию (АИЖК), экспортное страхование - ЭСКАР, венчурное финансирование - РВК, private equity – Роснано )

Регулирующие органы и центральный банк

• Государственные органы обеспечивают регулирование финансовой деятельности – устанавливают правила и следят за их выполнением.
• Банк России обеспечивает сейчас регулирование финансовой деятельности и выполняет функции центрального банка (концепция мега-регулятора)
• Центральный банк контролирует доступность денег и кредита с тем, чтобы обеспечить низкую инфляцию, экономический рост и стабильность финансовой системы.
• Министерство финансов РФ осуществляет регулирование отдельных сегментов (к примеру, аудиторов), обеспечивает регулирование в сфере бухгалтерского учета и отчетности (ПБУ - положения о бухгалтерском учете)
• Концепция мега-регулятора

Будущая стоимость (future value)

Рассмотрим подробнее принцип “Время имеет стоимость”.

Будущая стоимость – стоимость инвестиции, сделанной сегодня, на определенную будущую дату.

\[ FV = PV + PV i = PV (1+i) \]

\[ 1000 + 1000 (0.1) = 1100 \]

\[ FV_n = PV (1+i)^n \]

Капитализация процентов

Вопрос. Если вы положите 100 рублей на 3-летний вклад по ставке 10%, сколько вы получите денег через 3 года?

Лет	Расчет	Стоимость
1	\[100(1.1)\]	\[110\]
2	\[100(1.1)^2\]	\[121\]
3	\[100(1.1)^3\]	\[133,10\]

Вопрос. Какая будет сумма, если проценты начисляются не в конце каждого года, а ежемесячно?

Сложные проценты не “в годах”

Формула работает для любых периодов, просто нужно, чтобы \(i\) и \(n\) имели одинаковую размерность! Необходимо трансформировать годовую ставку в месячную.

Пусть \(i^m\) – процентная ставка в месяц, а n – количество месяцев.

тогда итоговая сумма при ежемесячном начислении будет определяется как

\[ (100) (1 + 0.1/12)^{12} = 110,47 \]

За счет ежемесячного начисления процентов вы получаете дополнительно 0,47 рублей

Непрерывно начисляемые доходности (сontinously compounded returns)

Начисление	Платежей	% за период
Ежегодно	1	0.1
Полгода	2	0.05
Квартал	4	0.025
Месяц	12	0.0083
Неделя	52	\(\frac{0.1}{52}\)
День	365	\(\frac{0.1}{365}\)
\(\infty\)	\(\infty\)

Непрерывно начисляемые доходности (сontinously compounded returns)

\[ 1105.517 = 1000 e^{0.1} \]

Общая формула для непрерывного начисления

\[ FV = PV e^{rn} \] \[ PV = \frac{FV}{e^{rn}}\]

Лог-доходность активов

Если мы поменяем в предыдущей формуле \(PV\) на стоимость актива в момент времени \(t\) (\(P_t\)) и зафиксируем единицу времени, тогда \(FV = P_{t+1}\), тогда

\[e^{r_t} = \frac{P_{t+1}}{P_t} \]

возьмем логарифм и получим сontinously compounded returns или лог-доходность актива:

\[ r_t = ln \frac{P_t}{P_{t-1}} = log(P_t) - log(P_{t-1}) \]

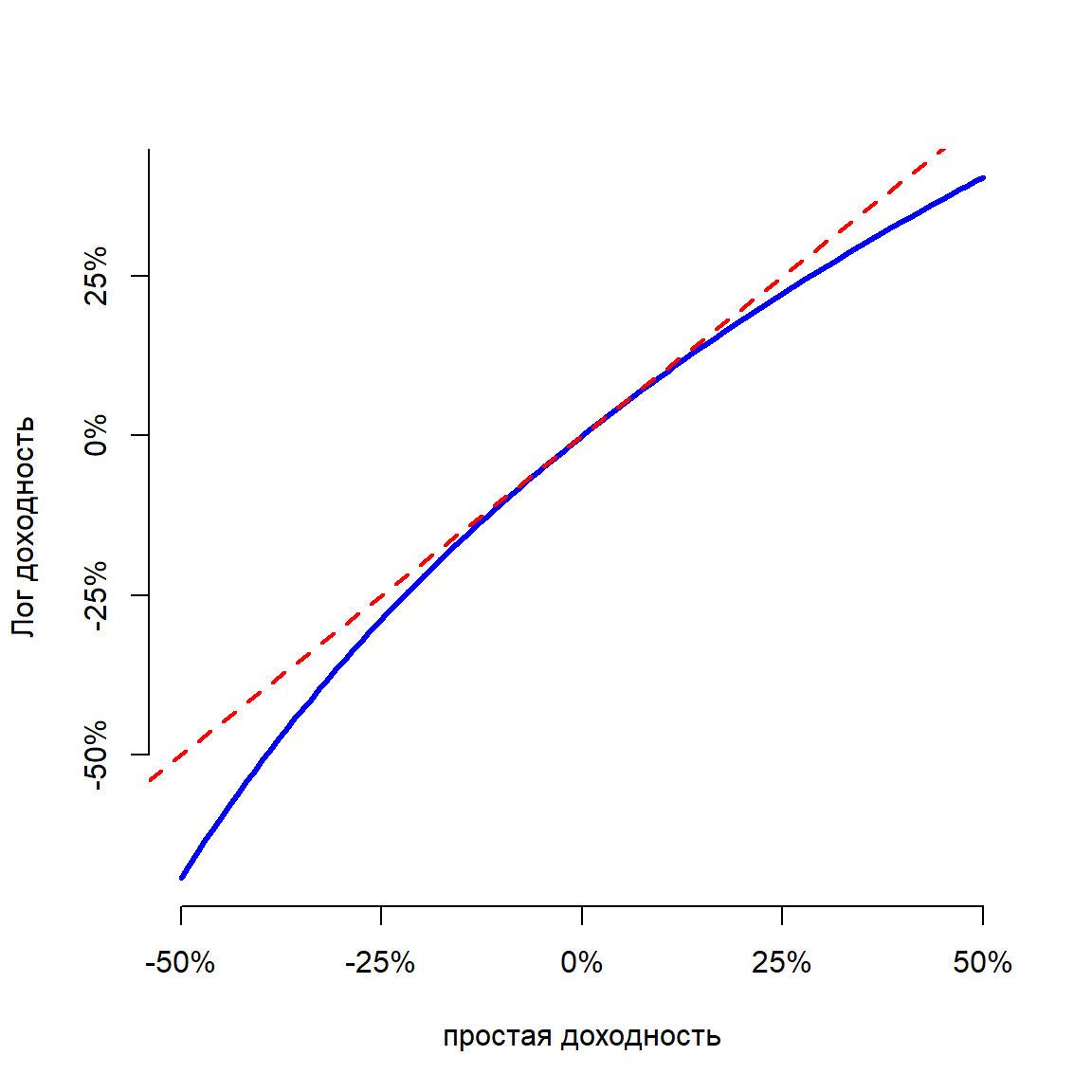
Лог-доходности примерно равны “обычным” доходностям при небольших значениях ставки, так как

\[ log(1+x) \approx x \]

Сравнение обычной и лог-доходностей

Преимущества лог-доходностей

Лог-доходности аддитивны. Доходность за несколько периодов – это просто суммма доходностей за каждый период.

Пример. Акция Газпрома выросла в цене в 2014 году на 50%, во 2015 году упала на 50%. Какова доходность за период 2014-2015?

Какова будет доходность в лог-доходностях?

Дополнительные преимущества – удобные статистические свойства. Поэтому в исследованиях стандартно используют расчеты в лог-доходностях. Практики финансовых рынков используют обычные доходности, так как даже малая ошибка округления недопустима.

Текущая стоимость (present value)

Текущая стоимость - стоимость, “приведенная” по состоянию на сегодня платежа, который должен быть осуществлен в определенный момент в будущем.

\[ PV = \frac{FV}{1+i} \] или для нескольких периодов

\[ PV = \frac{FV_n}{(1+i)^n} \]

Текущая стоимость выше, если:

1. Больше стоимость будущего потока платежей \(FV_n\)
2. Чем меньше времени до платежа \(n\)
3. Чем ниже процентная ставка \(i\)

Понятие риска в финансах – 1

• Риска избежать невозможно
• Любые экономические решения связаны с риском (К примеру, стоит ли покупать КАСКО на автомобиль или ограничиться ОСАГО? Стоит ли брать ипотеку сейчас или подождать?)
• Понимание риска в финансах – в отличие от других сфер жизни – связано с необходимостью измерения риска и оценки справедливой цены за перенос риска от одного участника к другому.

Понятие риска в финансах – 2

• Риск в финансах – это оценка меры неопределенности относительно будущих выплат в течение определенного времени относительно некоторого бенчмарка.
• Риск – величина, которая может быть оценена.
• Риск связан с неопределенностью будущего – мы не знаем точно, какой из будущих возможных вариантов развития событий осуществится.
• Риск связан с будущими выплатами – мы должны представить все возможные варианты и оценить их вероятности.

Понятие риска в финансах – 3

• Понимание риска в финансах относится к инвестиции или совокупности инвестиций. Инвестиции здесь понимаются широко.
• Риск должен измеряться в течение определенного временного периода. В общем случае риск меньше в короткие промежутки времени.
• Риск должен измеряться относительно бенчмарка – стандарта, а не в абсолютном выражении. К примеру, для акций обычно бенчмарк это фондовый индекс, для корпоративных облигаций – процентная ставка по госбумагам (безрисковый актив).

Вероятности и ожидаемая стоимость

• Теория вероятности говорит нам, что для того, чтобы оценить неопределенность, нам необходимо составить список всех возможных исходов и оценить вероятность (шансы) каждого из этих вариантов.
• Вероятность – это мера оценка возможности того, что событие произойдет. Вероятность находится между 0 (событие точно не произойдет) и 1 (событие точно произойдет).

Возможность	Вероятность	Исход
№1	1/2	Орел
№2	1/2	Решка

• Сумма вероятностей возможных исходов должна быть равна 1 по определению.

Вероятности и ожидаемая стоимость

• Инвестируем 1000 рублей в покупку акций Газпрома. Возможные исходы:

Возможность	Вероятность	Исход
№1	0,1	200
№2	0,4	700
№3	0,4	1300
№4	0,1	2000

Ожидаемая стоимость (математическое ожидание) = \[0,1 (200) + 0,4(700) + 0,4 (1300) + 0,1 (2000) = ? \]

Вероятности и ожидаемая стоимость

• Ожидаемые значения удобнее считать в доходностях (returns). Использование относительных мер (процентов) позволяет сравнивать доходности независимо от абсолютной суммы инвестиций.
• Изменчивость исходов приравнивается к риску.
• Безрисковый актив – это инвестиция, будущая стоимость которой известна и доходность которой не связана с риском (выплаты гарантированы и не могут измениться).

Дисперсия и среднеквадратическое отклонение

Дисперсия – это среднее квадратов отклонений возможных исходов от ожидаемого значения, взвешенных согласно их вероятности.

1. Рассчитать ожидаемое значение
2. Вычесть ожидаемое значение от каждого возможного исхода и возвести в квадрат
3. Умножить каждый исход на его вероятность
4. Сложить слагаемые

Среднеквадратическое отклонение (СКО) – квадратный корень дисперсии – имеет ту же размерность, что и исходные величины (проценты, рубли, доллары и проч.)

Если две инвестиции имеют одинаковую доходность, но разное СКО, мы предпочитаем инвестицию с меньшим значением СКО как менее рискованную.