Цели лекции

понять, в чем отличия финансовых данных от других типов данных
изучить основные источники финансовых данных, которые могут быть загружены в R
получить навыки трансформирования финансовых данных
изучить особенности расчета доходностей
разобраться, как и зачем осуществляется корректировка на выплаты дивидендов
изучить основные особенности финансовых данных с точки зрения статистики
понять, что такое стационарность временных рядов и почему это важно

Финансовые данные

Важность количественных методов в бизнесе и финансах увеличивается по мере того, как появляется большее количество информации и данных.
Финансовые данные систематически собираются в больших количествах и все с большей временной точностью. Достаточно большое количество финансовых данных доступно абсолютно бесплатно.
Финансовых данных как правило достаточно много по сравнению с другими областями. Вопрос обычно состоит не в том, что данных нет, а в том, чтобы эффективно использовать доступные данные и получить содержательные результаты.
В R есть множество пакетов, которые позволяют загружать финансовые данные напрямую. Вам не надо заходить куда-то в интернете, скачивать/экспортировать данные, сохранять их на свой компьютер, разбираться форматом хранения, загружать и проч. Обычно загрузка серии – это одна строка кода.
Основной пакет, который мы будем использовать для получения зарубежных данных финансовых серий – quantmod, для российских данных – QuantTools (данные ФИНАМа).
Источники бесплатных данных по финансовым рынкам – Yahoo Finance, Google Finance, FRED, Quandl, для России – Финам, Банк России, Московская Биржа.
Источники платных данных по финансовым рынкам – системы Bloomberg, Thomson Reuters (Eikon). Есть провайдеры данных только по ценам на финансовые активы – CQG, AlgoSeek, QuantQuote и другие.

Модель работы с количественными данными

Получение финансовых данных с помощью quantmod и QuantTools

## [1] "^GSPC"

## [1] "XOM"

library(quantmod) # загрузка пакет
getSymbols("^GSPC", src="yahoo", from ='1950-01-01') #  yahoo finance 
tail(GSPC)
library(QuantTools)
micex <- get_finam_data('MICEX', from = '2012-01-01', to = Sys.Date()) # индекс ММВБ 
# пакет QuantTools возвращает данные в формате data.table/data.frame, а не хts
class(micex)
micex <- quant_tools_to_xts(micex)
tail(micex)

Обычно у каждой серии есть свой уникальный идентификатор (id) – тикер – это текстовый код - аббревиатура. Но в разных источниках могут использоваться разные тикеры для одной и той же серии. Поэтому проверяйте тикеры, чтобы удостовериться, что источники возвращают вам те данные, что вам нужны. К примеру, индекс S&P 500 имеет тикер SPX в Bloomberg, ^GSPC – в Yahoo Finance, INDEXSP:.INX – в Google Finance, SP500 – во FRED.

Получение данных из Quandl

Сервис Quandl представляет собой удобный сервис для доступа к разным наборам финансовых/экономических данных “в одном месте”. Существуют как платные, так и бесплатные датасеты.
Для того, чтобы получать данные с Quandl необходимо зарегестрироваться на сайте и получать свой уникальный ключ доступа (API Key)

require(Quandl)

# Crude Oil Futures, Continuous Contract #31 (CL31)
#Quandl.api_key("BLQfNYvHf1E6vFusHAT4")# ваш собcтвенный API Key
#cl <-  Quandl("EIA/PET_RWTC_D")

построим график полученной серии

head(cl,10)

         Date Value
1  2018-11-05 63.12
2  2018-11-02 63.12
3  2018-11-01 63.67
4  2018-10-31 65.31
5  2018-10-30 66.18
6  2018-10-29 67.00
7  2018-10-26 67.58
8  2018-10-25 67.25
9  2018-10-24 66.56
10 2018-10-23 66.49

plot(x = cl$Date, y = cl$Value, type = 'l', ylab ='$/баррель', xlab = "", 
     main = 'Динамика цен на нефть WTI')

Данные Alpha Vantage

[1] "MSFT"

           MSFT.Open MSFT.High MSFT.Low MSFT.Close MSFT.Volume
2019-11-05    144.97    145.02   143.91     144.46    18250200
2019-11-06    144.37    144.52   143.20     144.06    16575800
2019-11-07    143.84    144.88   143.77     144.26    17786700
2019-11-08    143.98    145.99   143.76     145.96    16732700
2019-11-11    145.34    146.42   144.73     146.11    14362600
2019-11-12    146.28    147.57   146.06     147.07    18641600

Чтение данных из заранее сохраненных файлов

Формат .csv является наиболее простым и распространенным вариантам хранения небольших объемов финансовых данных. Файл csv (comma separated values) является просто текстовым файлом, в котором записана таблица данных (обычно использется запятая для того, чтобы разделить данные из разных столбцов)
В R используются команды write.csv и read.csv для записи и чтения файлов csv
У вас также есть возможность читать/записывать данные в формат Excel, но лучше это делать для итогового варианта и не использовать Excel для хранения исходных данных.
Вы можете подготовить необходимые данные в Excel, экспортировать их в csv, а потом прочитать csv-файл в R.
Для чтения больших файлов csv лучше использовать специальных функции fread/fwrite из пакета data.table.

#write.csv(GSPC, 'data/sp500.csv', row.names = FALSE ) 
sp500 = read.csv('data/sp500.csv', stringsAsFactors = FALSE)
# по умолчанию R записывает названия столбцов (row names). если не указано иное, это просто нумерация строк # по порядку - 1,2, 3 и так далее. Нам не нужен столбец, поэтому row.name = FALSE
str(sp500)

'data.frame':   17580 obs. of  7 variables:
 $ GSPC.Open    : num  16.7 16.9 16.9 17 17.1 ...
 $ GSPC.High    : num  16.7 16.9 16.9 17 17.1 ...
 $ GSPC.Low     : num  16.7 16.9 16.9 17 17.1 ...
 $ GSPC.Close   : num  16.7 16.9 16.9 17 17.1 ...
 $ GSPC.Volume  : num  1260000 1890000 2550000 2010000 2520000 2160000 2630000 2970000 3330000 1460000 ...
 $ GSPC.Adjusted: num  16.7 16.9 16.9 17 17.1 ...
 $ date         : chr  "1950-01-03" "1950-01-04" "1950-01-05" "1950-01-06" ...

Как мы уже знаем, команда str показывает структуру объекта и указывает, что необходимо изменить формат столбца data из-за того, что он имеет тип factor.

Чтение/запись данных из фойлов Excel

В R существует несколько пакетов для работы с файлами Excel. Я рекомендую использовать пакет readxl, если вам нужно только прочитать данные из Excel и пакет openxlsx, если вам необходимо записывать

        Period  M:AR M:AU M:BR M:CA  M:CH M:CL M:CN M:CO M:CZ  M:DK M:GB M:HK
868 2018-04-30 30.25  1.5  6.5 1.25 -0.75  2.5 4.35 4.25 0.75 -0.65 0.50 2.00
869 2018-05-31 40.00  1.5  6.5 1.25 -0.75  2.5 4.35 4.25 0.75 -0.65 0.50 2.00
870 2018-06-30 40.00  1.5  6.5 1.25 -0.75  2.5 4.35 4.25 1.00 -0.65 0.50 2.25
871 2018-07-31 40.00  1.5  6.5 1.50 -0.75  2.5 4.35 4.25 1.00 -0.65 0.50 2.25
872 2018-08-31 60.00  1.5  6.5 1.50 -0.75  2.5 4.35 4.25 1.25 -0.65 0.75 2.25
873 2018-09-30 65.00  1.5  6.5 1.50 -0.75  2.5 4.35 4.25 1.50 -0.65 0.75 2.50
    M:HR M:HU M:ID M:IL M:IN M:IS M:JP M:KR M:MK M:MX M:MY M:NO M:NZ M:PE M:PH
868 0.25  0.9 4.25  0.1 6.00 4.25 -0.1  1.5 3.00 7.50 3.25 0.50 1.75 2.75 3.00
869   NA  0.9 4.75  0.1 6.00 4.25 -0.1  1.5 3.00 7.50 3.25 0.50 1.75 2.75 3.25
870   NA  0.9 5.25  0.1 6.25 4.25 -0.1  1.5 3.00 7.75 3.25 0.50 1.75 2.75 3.50
871 0.00  0.9 5.25  0.1 6.25 4.25 -0.1  1.5 3.00 7.75 3.25 0.50 1.75 2.75 3.50
872   NA  0.9 5.50  0.1 6.50 4.25 -0.1  1.5 2.75 7.75 3.25 0.50 1.75 2.75 4.00
873   NA  0.9 5.75  0.1 6.50 4.25 -0.1  1.5 2.75 7.75 3.25 0.75 1.75 2.75 4.50
    M:PL M:RO M:RS M:RU M:SA M:SE M:TH  M:TR  M:US M:XM M:ZA
868  1.5 2.25    3 7.25 2.25 -0.5  1.5  8.00 1.625    0  6.5
869  1.5 2.50    3 7.25 2.25 -0.5  1.5  8.00 1.625    0  6.5
870  1.5 2.50    3 7.25 2.50 -0.5  1.5 17.75 1.875    0  6.5
871  1.5 2.50    3 7.25 2.50 -0.5  1.5 17.75 1.875    0  6.5
872  1.5 2.50    3 7.25 2.50 -0.5  1.5 17.75 1.875    0  6.5
873  1.5 2.50    3 7.50 2.75 -0.5  1.5 24.00 2.125    0  6.5

Индекс S&P 500 – долгосрочная динамика фондового рынка

Наиболее простой и популярный тип визуализации финансовых данных – график временного ряда, где по оси Х находятся время, по оси Y – значение

График OHLC

Часто визуальное предоставление финансовых серий осуществляется с помощью графиков OHLC (Open - High - Low - Close)

library(quantmod)
quantmod::candleChart(GSPC['2019::'], theme = 'white', name = 'Индекс S&P500 в 2019 году')

tail(GSPC)

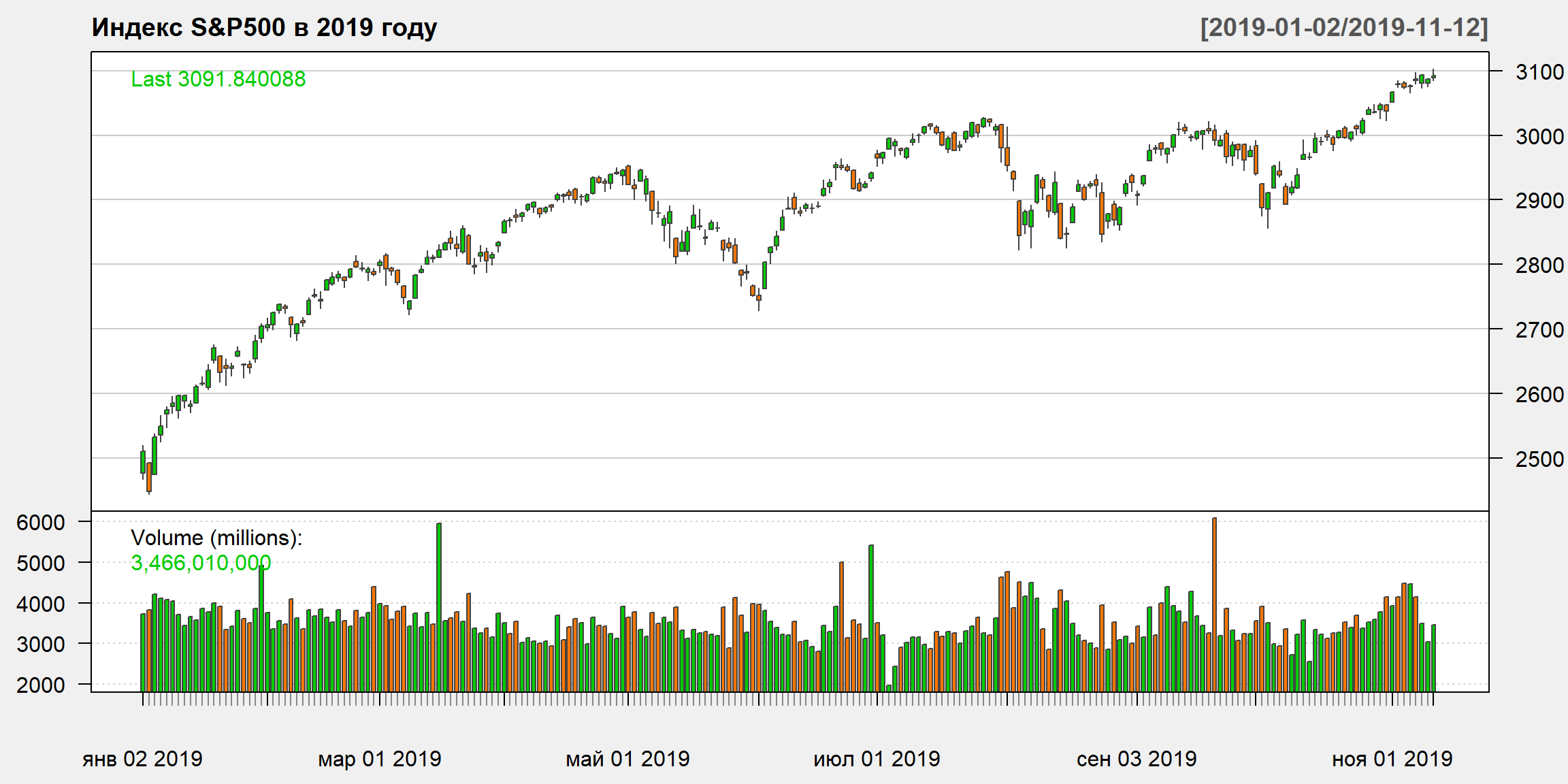
           GSPC.Open GSPC.High GSPC.Low GSPC.Close GSPC.Volume GSPC.Adjusted
2019-11-05   3080.80   3083.95  3072.15    3074.62  4486130000       3074.62
2019-11-06   3075.10   3078.34  3065.89    3076.78  4458190000       3076.78
2019-11-07   3087.02   3097.77  3080.23    3085.18  4144640000       3085.18
2019-11-08   3081.25   3093.09  3073.58    3093.08  3499150000       3093.08
2019-11-11   3080.33   3088.33  3075.82    3087.01  3035530000       3087.01
2019-11-12   3089.28   3102.61  3084.73    3091.84  3466010000       3091.84

Open – цена открытия (начало торгового дня)
High – максимальная цена за период
Low – минимальная цена за период
Close – цена закрытия
Volume – цена закрытия
Adjusted – цена закрытия с учетом корректировок на выплату дивидендов и разделение (split) акций

Вариант графика OHLC – bar chart

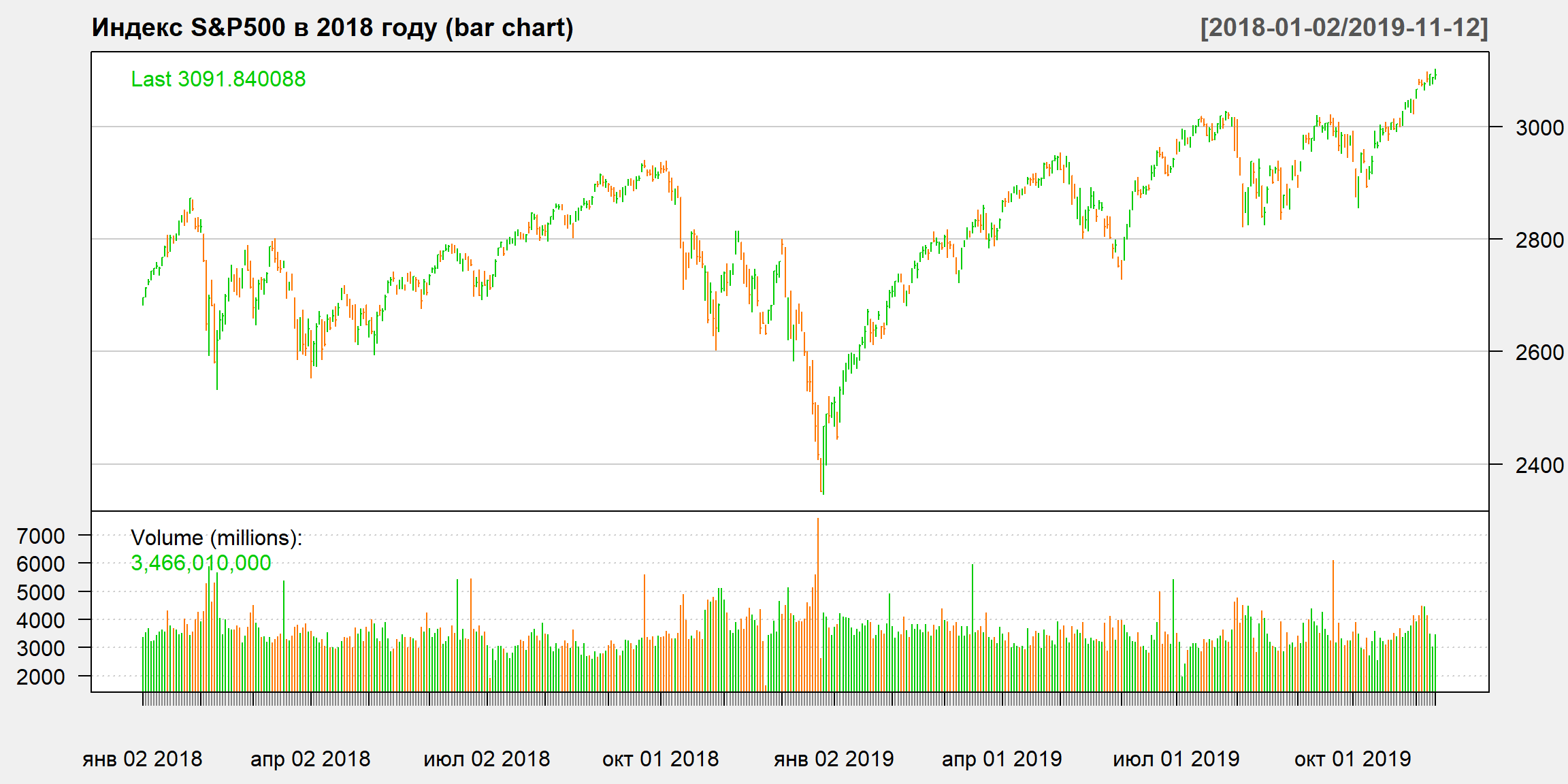
barChart(GSPC['2018::'], theme = 'white', name = 'Индекс S&P500 в 2018 году (bar chart)')

Внутридневные (intraday) данные

Для дневных серий обычно используют цены закрытия торгового дня (close price). Обратите внимание, что время закрытия для разных торговых площадок может отличаться. Пример – оценка корреляции между ценой на нефть WTI на NYMEX (время закрытия – 21-30 по МСК) и курсом RUB/USD (фиксинг - 12-00 МСК предыдущего дня, время основной сессии на Московской Бирже – c 10-00 до 15-15 и так далее). Эти различия имеют значение на современных рынках.
Финансовые данные зачастую доступны с очень высоким разрешением – вплоть до мониторинга данных по каждым отдельным торговым операциям (tick data)
Многие современные финансовые рынки функционируют в круглосуточном режиме. К примеру, валютные рынки устроены подобным образом.
Скорость обработки информации за последние 10-15 лет выросла драматическим образом. Поэтому реакция рынки на те или иные события очень быстрая. Использование дневных данных не позволяет оценивать эти эффекты.
Как правило, у вас нет ограничений использовать только дневные данные, внутридневные данные доступны в специализированных системах и базах данных, иногда – бесплатно.
Внутридневные данные занимают много места и требуют много вычислительных ресурсов для обработки.

Торговля RUB/USD на прошлой неделе - данные за каждые 15 минут

Используем пакет QuantTools для доступа к данным валютной секции ММВБ
Sys.Date() – это текущая дата (то есть, сегодня), Sys.Date()-5 – это пять дней назад.

require(QuantTools)
rub = get_finam_data('USDRUB', from = Sys.Date()-5, to = Sys.Date(), period = "15min")
rub = quant_tools_to_xts(rub)
quantmod::candleChart(rub, theme='white', name = 'Динамика торгов долларом США \n на прошлой неделе')

Преобразование данных – изменение периодичности

Чаще все в рамках построения финансовых моделей мы не работаем не с исходными данными непосредственно, а осуществляем преобразования данных для того, чтобы привести их в нужную форму. Преобразования могут быть следующими:

Переход от дневных к месячным/недельным данным или от внутридневных данных – к дневным. Можно перейти от данных меньшей размерности – к большей, но не наоборот. То есть, к примеру, невозможно перейти от недельных данных – к дневным.
Функции to.xxx из пакета xts позволяют легко осуществлять подобные преобразования. Для данных OHLC функция осуществляет корректный расчет максимальных/минимальных значений за период, а также величины объемы торгов (столбец Volume)

periodicity(GSPC) # исходная перодичность данных

Daily periodicity from 1950-01-03 to 2019-11-12

tail(to.monthly(GSPC))

         GSPC.Open GSPC.High GSPC.Low GSPC.Close GSPC.Volume GSPC.Adjusted
июн 2019   2751.53   2964.15  2728.81    2941.76 70904280000       2941.76
июл 2019   2971.41   3027.98  2952.22    2980.38 70349470000       2980.38
авг 2019   2980.32   3013.59  2822.12    2926.46 79599440000       2926.46
сен 2019   2909.01   3021.99  2891.85    2976.74 73992330000       2976.74
окт 2019   2983.69   3050.10  2855.94    3037.56 77564550000       3037.56
ноя 2019   3050.72   3102.61  3050.72    3091.84 31166700000       3091.84

tail(to.quarterly(GSPC))

        GSPC.Open GSPC.High GSPC.Low GSPC.Close  GSPC.Volume GSPC.Adjusted
2018 Q3   2704.95   2940.91  2698.95    2913.98 196272470000       2913.98
2018 Q4   2926.29   2939.86  2346.58    2506.85 254930610000       2506.85
2019 Q1   2476.96   2860.31  2443.96    2834.40 229181340000       2834.40
2019 Q2   2848.63   2964.15  2728.81    2941.76 217369240000       2941.76
2019 Q3   2971.41   3027.98  2822.12    2976.74 223941240000       2976.74
2019 Q4   2983.69   3102.61  2855.94    3091.84 108731250000       3091.84

Преобразование данных – изменение периодичности

Выбор определенного периода времени для анализа. Объекты типа xts позволяют осуществлять выборку данных внутри квадратных скобок

head(GSPC['2017']) # весь 2017 год

           GSPC.Open GSPC.High GSPC.Low GSPC.Close GSPC.Volume GSPC.Adjusted
2017-01-03   2251.57   2263.88  2245.13    2257.83  3770530000       2257.83
2017-01-04   2261.60   2272.82  2261.60    2270.75  3764890000       2270.75
2017-01-05   2268.18   2271.50  2260.45    2269.00  3761820000       2269.00
2017-01-06   2271.14   2282.10  2264.06    2276.98  3339890000       2276.98
2017-01-09   2273.59   2275.49  2268.90    2268.90  3217610000       2268.90
2017-01-10   2269.72   2279.27  2265.27    2268.90  3638790000       2268.90

tail(GSPC['/2017']) # все по 2017 год

           GSPC.Open GSPC.High GSPC.Low GSPC.Close GSPC.Volume GSPC.Adjusted
2017-12-21   2683.02   2692.64  2682.40    2684.57  3273390000       2684.57
2017-12-22   2684.22   2685.35  2678.13    2683.34  2399830000       2683.34
2017-12-26   2679.09   2682.74  2677.96    2680.50  1968780000       2680.50
2017-12-27   2682.10   2685.64  2678.91    2682.62  2202080000       2682.62
2017-12-28   2686.10   2687.66  2682.69    2687.54  2153330000       2687.54
2017-12-29   2689.15   2692.12  2673.61    2673.61  2443490000       2673.61

head(GSPC['2017/2017-03']) # c январь по март 2017 года

           GSPC.Open GSPC.High GSPC.Low GSPC.Close GSPC.Volume GSPC.Adjusted
2017-01-03   2251.57   2263.88  2245.13    2257.83  3770530000       2257.83
2017-01-04   2261.60   2272.82  2261.60    2270.75  3764890000       2270.75
2017-01-05   2268.18   2271.50  2260.45    2269.00  3761820000       2269.00
2017-01-06   2271.14   2282.10  2264.06    2276.98  3339890000       2276.98
2017-01-09   2273.59   2275.49  2268.90    2268.90  3217610000       2268.90
2017-01-10   2269.72   2279.27  2265.27    2268.90  3638790000       2268.90

Преобразование данных – первые/последние элементы

Функции xts::first и xts::last позволяют вам получить первые или последние элементы объекта xts. Второй аргумент фукнций позволяет задавать количество периодов, которое нам необходимо.
Названия функций first/last используются в других пакетах, поэтому используется синтаксис xts::first. Это означает использовать функцию first именно из пакета xts.

xts::last(GSPC, '1 week') ## последняя неделя

           GSPC.Open GSPC.High GSPC.Low GSPC.Close GSPC.Volume GSPC.Adjusted
2019-11-11   3080.33   3088.33  3075.82    3087.01  3035530000       3087.01
2019-11-12   3089.28   3102.61  3084.73    3091.84  3466010000       3091.84

xts::last(GSPC, '3 days') ## последние три дня

           GSPC.Open GSPC.High GSPC.Low GSPC.Close GSPC.Volume GSPC.Adjusted
2019-11-08   3081.25   3093.09  3073.58    3093.08  3499150000       3093.08
2019-11-11   3080.33   3088.33  3075.82    3087.01  3035530000       3087.01
2019-11-12   3089.28   3102.61  3084.73    3091.84  3466010000       3091.84

Преобразование данных – логарифм

Используйте лог-преобразование для того, чтобы скорректировать серию на экспоненциальный рост и “ограничить” волатильность.

Параметр mfrow = c(nrow, ncols) отвечает за комбинирование графиков на одном листе. Команда создает матрицу из nrows строк и ncolsстолбцов, которая заполняется графиками по строкам.

Регрессия логарифма S&P по времени

Посчитаем простую линейную регрессию зависимости абсолютного лог-значения индекса SP500 от времени c помощью функции lm.

head(data)

  GSPC.Adjusted       date
1         16.66 1950-01-03
2         16.85 1950-01-04
3         16.93 1950-01-05
4         16.98 1950-01-06
5         17.08 1950-01-09
6         17.03 1950-01-10

names(data)[1] <- 'sp500'
data$sp500.log <- log(data$sp500)
time <- 1:nrow(data)
model.time <- lm(data$sp500.log ~ time)
summary(model.time)


Call:
lm(formula = data$sp500.log ~ time)

Residuals:
    Min      1Q  Median      3Q     Max 
-0.7203 -0.1804  0.0084  0.1927  0.7576 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 3.098e+00  4.181e-03   741.1   <2e-16 ***
time        2.750e-04  4.119e-07   667.7   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.2771 on 17578 degrees of freedom
Multiple R-squared:  0.9621,    Adjusted R-squared:  0.9621 
F-statistic: 4.458e+05 on 1 and 17578 DF,  p-value: < 2.2e-16

Сравним фактические данные и модельную регрессию:

Может ли вчерашнее значение индекса предсказать нам значение сегодня?

data$sp500.lag.log <- c(NA, lag(data$sp500.log)[-nrow(data)])
fancy.plot(data$sp500.lag.log, data$sp500.log, cex=0.5, col=2, xlab="Значение вчера Log(S&P 500)", ylab="Значение сегодня Log(Dow)", asp=1)

Может ли вчерашнее значение индекса предсказать нам значение сегодня? (2)

Посчитаем регрессию

model.yest <- lm(data = data, sp500.log ~ sp500.lag.log)
print(summary(model.yest), digits=6)


Call:
lm(formula = sp500.log ~ sp500.lag.log, data = data)

Residuals:
        Min          1Q      Median          3Q         Max 
-0.22928975 -0.00433294  0.00017769  0.00464371  0.10932150 

Coefficients:
                 Estimate  Std. Error     t value Pr(>|t|)    
(Intercept)   4.97267e-04 2.91272e-04     1.70723 0.087797 .  
sp500.lag.log 9.99964e-01 5.11381e-05 19554.16651  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.00964641 on 17577 degrees of freedom
  (1 observation deleted due to missingness)
Multiple R-squared:  0.999954,  Adjusted R-squared:  0.999954 
F-statistic: 3.82365e+08 on 1 and 17577 DF,  p-value: < 2.22e-16

confint(model.yest)

                      2.5 %      97.5 %
(Intercept)   -0.0000736543 0.001068189
sp500.lag.log  0.9998634788 1.000063950

Похоже, что не очень. Согласно посчитанной регрессии, “сегодня” будет таким же, как вчера ($\beta = 1$).

! В финансовых данных обычно наблюдения, которые находятся “рядом”" другом с другом, скоррелированны между собой.

Гистограмма лог-значений – проверка допущений

Гистограмма указывает на то, что моменты распределения не являются устойчивыми. Использование данных в такой форме (“в уровнях”) не очень осмысленно.

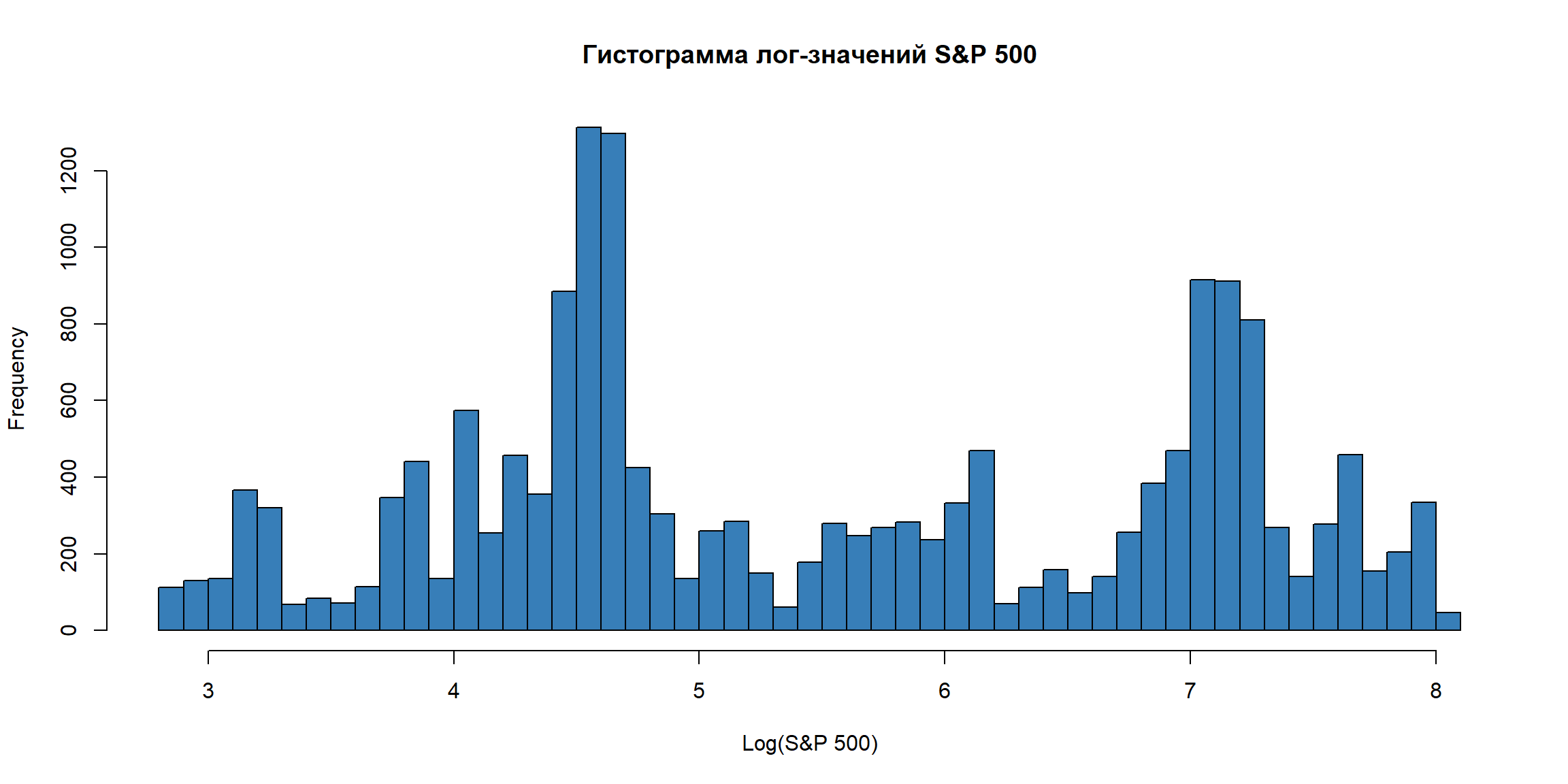
Может быть, надо преобразовать значения серии?

Доходность

Доходность – лог-значение “сегодня” минус лог-значение “вчера” или лог-доходность

data$sp500.ret <- data$sp500.log - data$sp500.lag.log
fancy.plot(data$date, data$sp500.ret, t="l", xlab="Дата", ylab="Лог-доходность", col=2)

#diff(log(GSPC$GSPC.Close)) - расчет лог-доходности для объектов xts

Нетто-доходность

Пусть $P_t$ это цена финансового актива в момент времени $t$. Если мы предположим, что в этот период не было выплат дивидендов, то нетто-доходность за период владения со времени $t-1$ до времени $t$ составит

\[ R_t = \frac{P_t}{P_{t-1}} -1 = \frac{P_t - P_{t-1}}{P_{t-1}} \]

Числитель – прибыль, полученная за период владения, отрицательное значение означает убыток.

Знаменатель – первоначальная инвестиция, сделанная в начале периода владения. Минимальное значение доходности = -1, то есть 100% убыток или потеря всей первоначальной инвестиции.

\[ R_t \geq -1 \]

Валовая доходность

Валовая доходность определяется как:

\[ \frac{P_t}{P_{t-1}} = 1 + R_t \]

Доходности не зависят от размерности исходных величин (доллары, рубли и проч.) Размерность доходности – время. Она зависит от единиц $t$ (час, день, неделя, год).

Валовая доходность за последние $k$ периодов является произведением доходностей за каждый из периодов:

\[ 1 + R_t(k) = \frac{P_t}{P_{t-k}} = (\,\frac{P_t}{P_{t-1}})\,(\frac{P_{t-1}}{P_{t-2}}) ... (\frac{P_{t-k+1}}{P_{t-k}}) \]

Лог-доходность (continuously compounded return)

Лог-доходность или continuously compounded returns определяются как:

\[ r_t = log(1 + R_t) = log(\frac{P_t}{P_{t-1}}) = p_t - p_{t-1} \]

где $p_t = log(P_t)$ – лог-цена.

Лог-доходности примерно равны доходностям из-за того, что если $x$ достаточно малая величина, то $log(1+x) \approx x$

Чем более короткий промежуток времени (дни, часы, минуты) мы используем, тем меньше будет доходность меньше по абсолютным значениям.Поэтому мы можем ожидать, что доходности будут примерно равно лог-доходностям для дневных и внутридневных данных. Для годовых данных, к примеру, ошибка будет гораздо больше – для них не стоит использовать такое преобразование.
Доходности и лог-доходности имеют одинаковый знак
Лог-доходности на всех промежутках значениях больше простой доходности. По мере приближения обычной доходности к -1 (потеря всех инвестиций), лог-доходность стремится к $-\infty$

Корректировка на дивиденды для акций

Многие компании, особенно из традиционных секторов, платят дивиденды, которые должны быть учтены при оценке полной доходности (total return).
Если мы не учитываем эту компоненту, то мы рискуем неправильно оценивать доходности для инвесторов и исказить результаты анализа.
Иногда компании проводят разделение акций (stock split), то есть обмен “старых” акций на “новые” в определенном соотношении. К примеру, каждый владелец 1 старой акции получает 2 новых. В этих операциях нет экономической сути, они делаются просто для удобства котирования цен и/или по историческим причинам.

Акции Exxon Mobil - 1

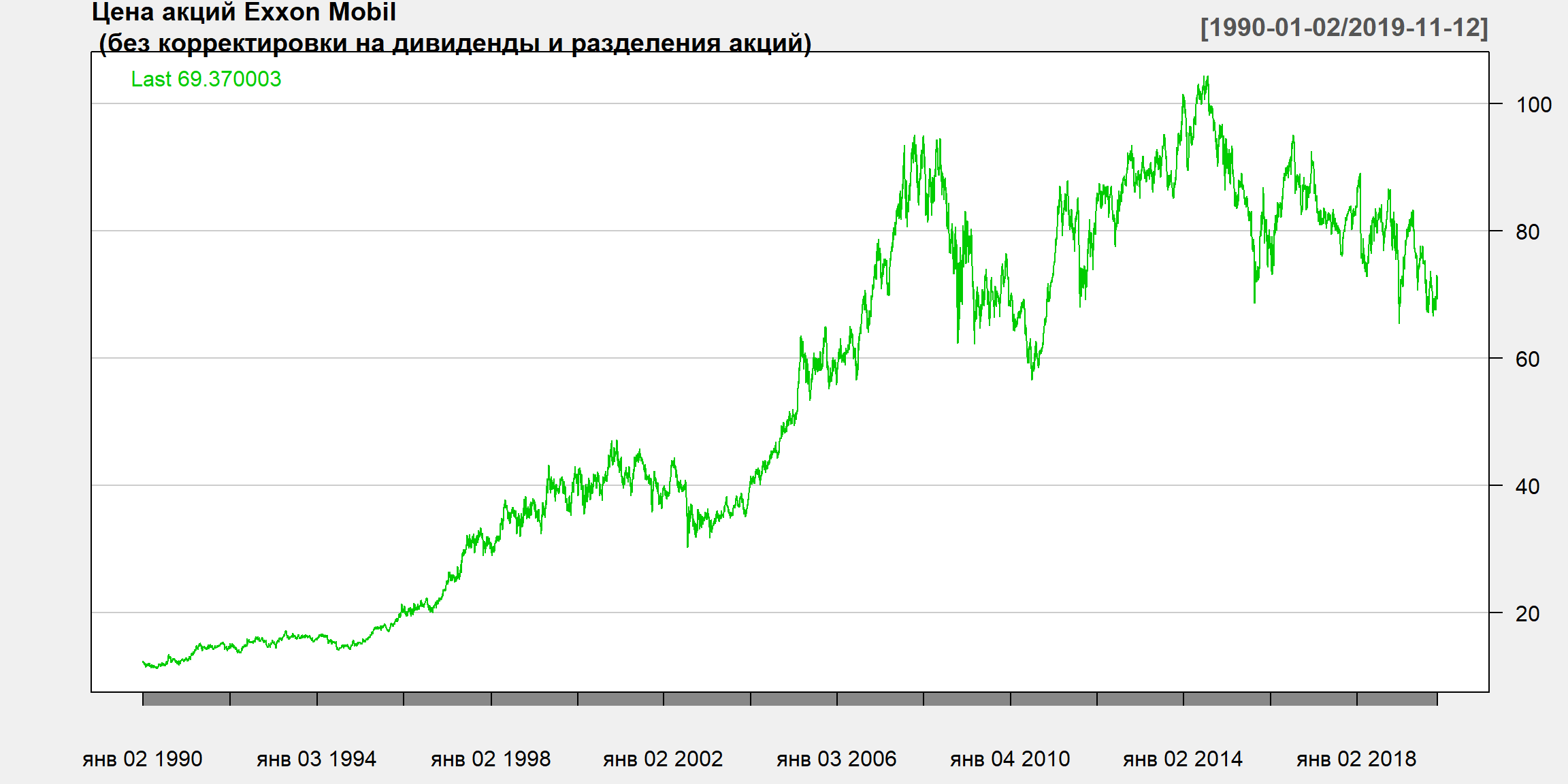
Акции Exxon Mobil - 2

Порядок корректировки цены акции на дивиденды

Если дивиденды выплачиваются до периода времени $t$, то валовая доходность в момент времени $t$ определяется как

\[ 1+ R_t = \frac{P_t + D_t}{P_{t-1}} = \frac{P_t}{P_{t-1}} + \frac{D_t}{P_{t-1}} \]

Нетто-доходность будет $r_t = log(1+R_t) = log(P_t + D_t) - log(P_{t-1})$.

Для дневных доходностей, дивидендная доходность равна нулю во все дни, когда не выплачиваются дивиденды. Для компаний, которые не выплачивают дивиденды, полная доходность и ценовая доходность равны друг другу.
Для скорректированной (adjusted) цены акции стоимость дивидендов вычитается из цены закрытия на дату “отсечки”. Дата “отсечки” – последняя дата, на которую признается право акционера на получение дивидендов.
Предположим, что цена закрытия акций Роснефти составила 300 рублей в четверг. После закрытия торгов Роснефть объявила о том, что выплатит дивиденды в размере на 10 рублей на акцию. Тогда скорректированная цена акции составит 290 рублей = 300 - 10.
Корректировка на дивиденды “меняет”" цены в прошлом. Текущая скорректированная цена и текущая цена на рынке должны быть равны другу другу. Поэтому корректируются именно исторические данные, а не текущие.

Полная доходность (total return) для акций Газпрома

Для многих российских бумаг, разница между полной доходностью и ценовой доходностью также важна!
В Bloomberg можно оценивать total return для российских бумаг

К сожалению, доступные бесплатные источники не предоставляют информацию по полной доходности для российских активов. Bloomberg предоставляет данные по дивидендам и total return для российских бумаг.

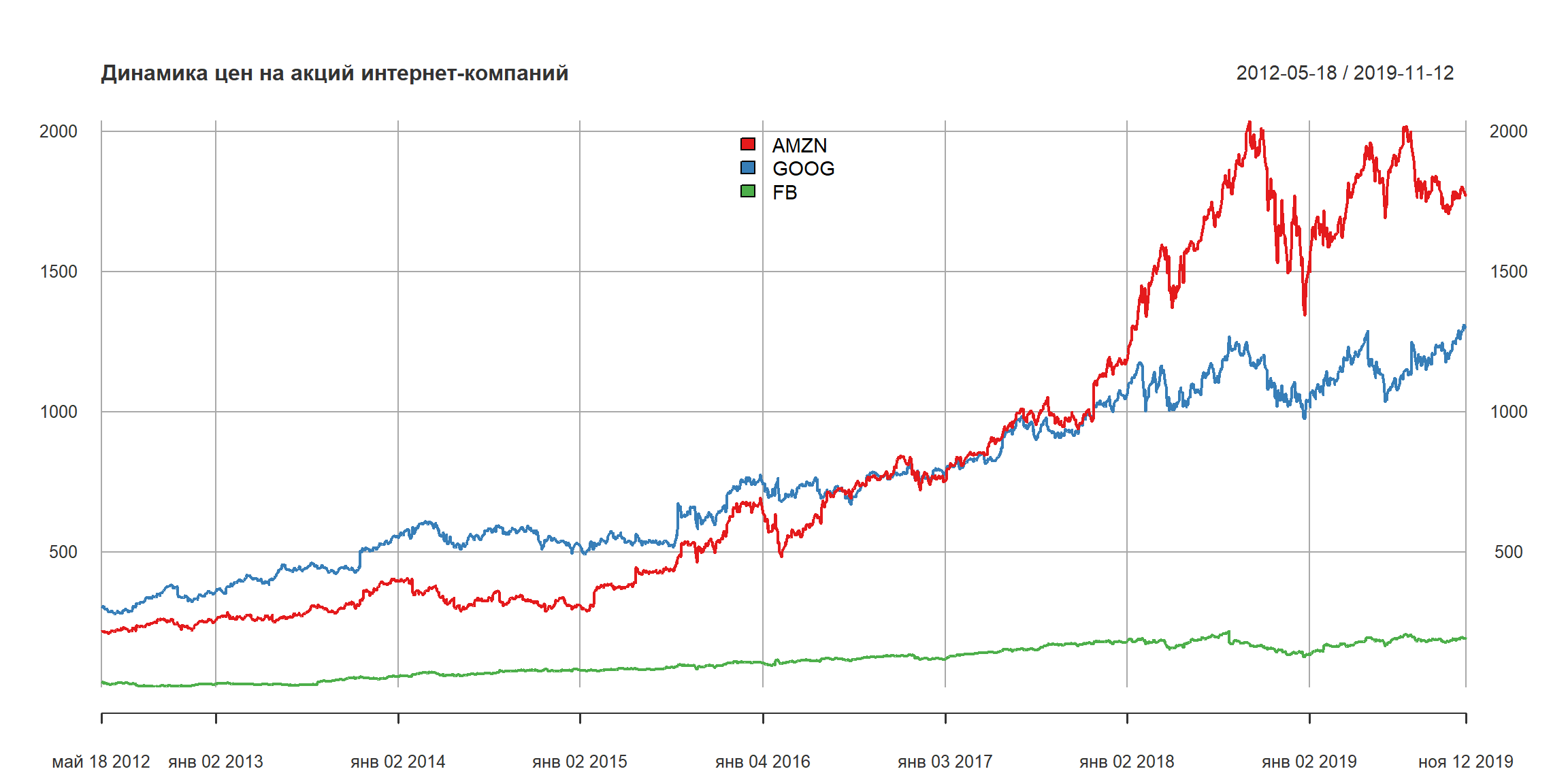
Сравнение доходностей нескольких бумаг за период времени

нарисуем график трех бумаг – Amazon, Google и Facebook. Акции Facbook торгуются с мая 2012 года (IPO). Поэтому график начинается с 18 мая 2012 года.

[1] "AMZN" "GOOG" "FB"

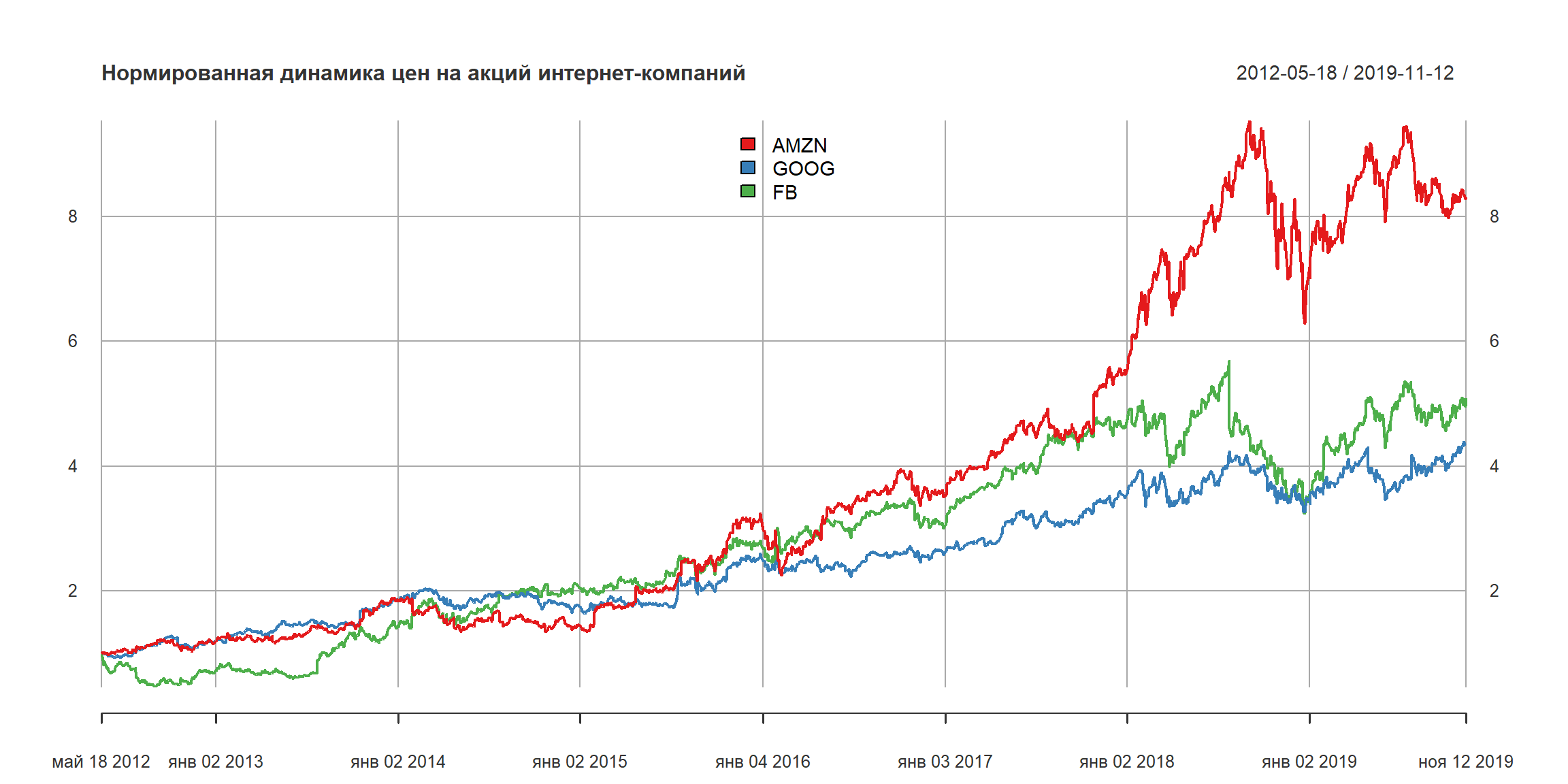
нормируем график по состоянию на 18 мая 2012 года – поделим значения каждой бумаги на соответствующее значение в этот день:

library(xts)
tech_stocks2 <- tech_stocks
tech_stocks2$AMZN <- tech_stocks2$AMZN / as.numeric(xts::first(tech_stocks2$AMZN))
tech_stocks2$GOOG <- tech_stocks2$GOOG / as.numeric(xts::first(tech_stocks2$GOOG))
tech_stocks2$FB <- tech_stocks2$FB / as.numeric(xts::first(tech_stocks2$FB))

plot.xts(tech_stocks2,legend.loc = 'top', main = 'Нормированная динамика цен на акций интернет-компаний')

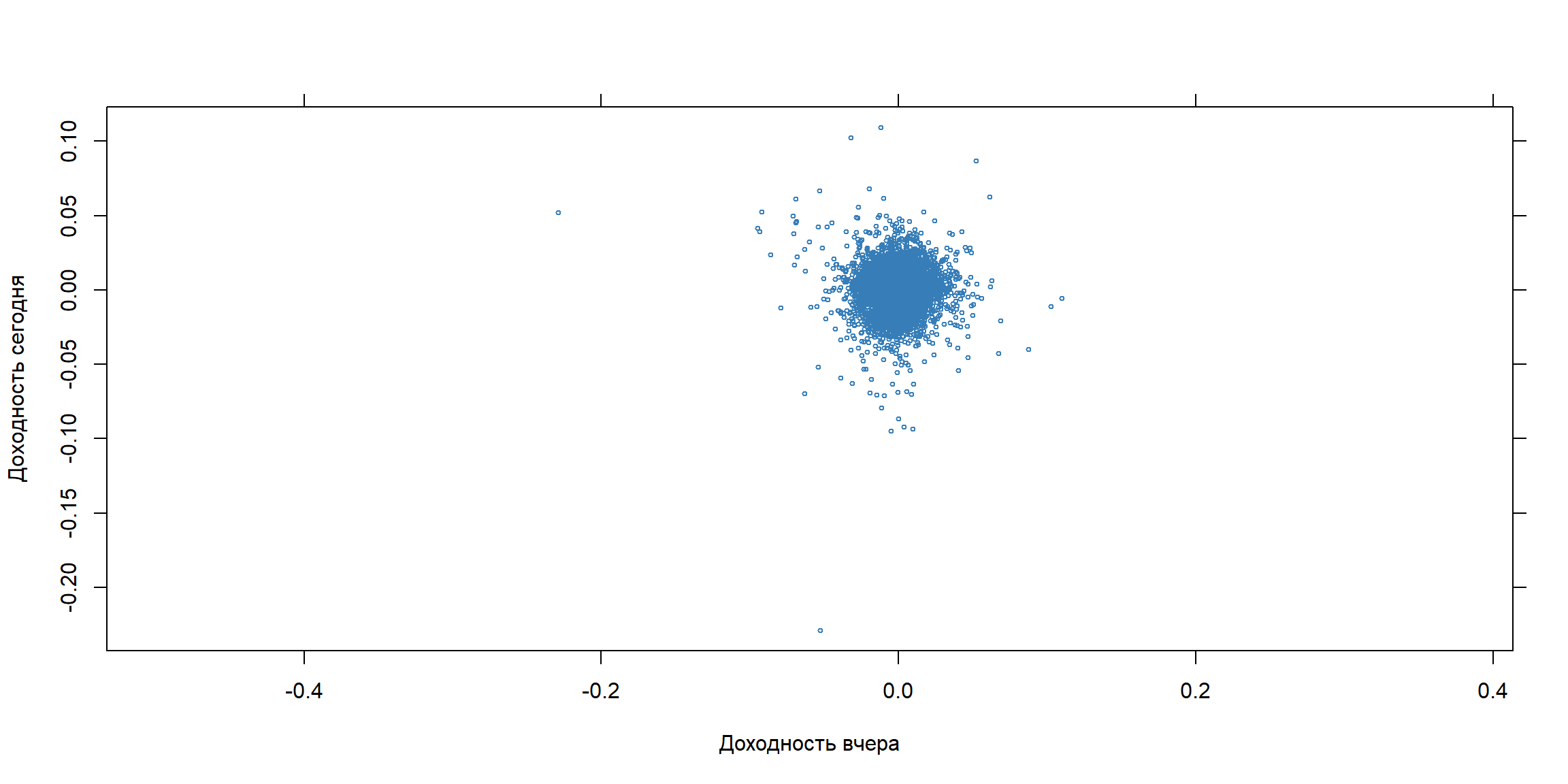
Позволяет ли доходность вчера предсказать доходность сегодня?

Позволяет ли доходность вчера предсказать доходность сегодня? (2)

посчитаем регрессию для доходностей

model.ret <- lm(data = data, sp500.ret ~ sp500.ret.lag)
summary(model.ret, digits = 4)


Call:
lm(formula = sp500.ret ~ sp500.ret.lag, data = data)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.227941 -0.004305  0.000185  0.004646  0.109583 

Coefficients:
               Estimate Std. Error t value Pr(>|t|)    
(Intercept)   2.890e-04  7.277e-05   3.971 7.18e-05 ***
sp500.ret.lag 2.539e-02  7.540e-03   3.367 0.000762 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.009643 on 17576 degrees of freedom
  (2 observations deleted due to missingness)
Multiple R-squared:  0.0006446, Adjusted R-squared:  0.0005877 
F-statistic: 11.34 on 1 and 17576 DF,  p-value: 0.0007617

Гистограмма доходностей – похожа на нормальное распределение?

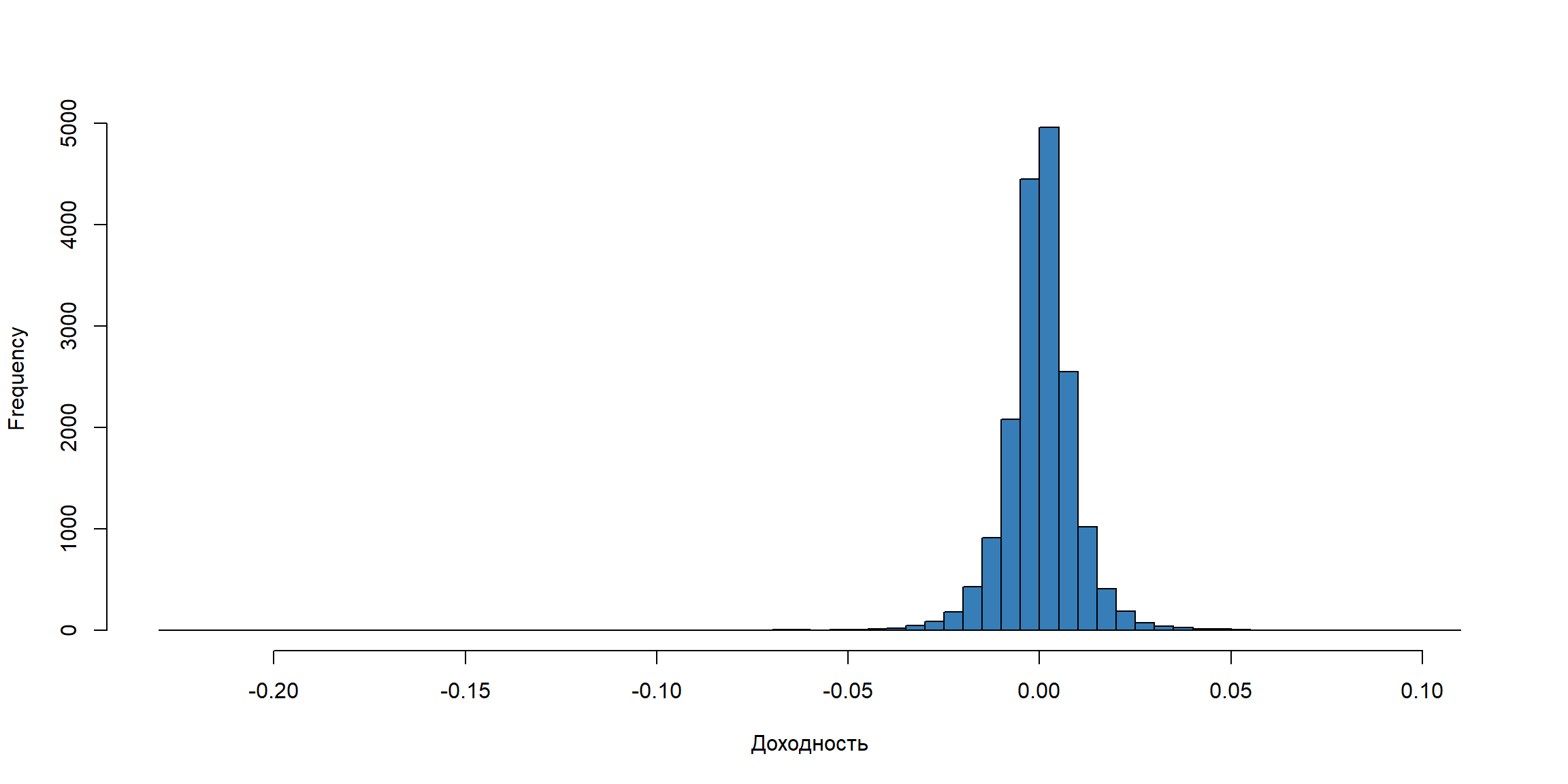
hist(data$sp500.ret, breaks=100, col=2, xlab="Доходность", main="")

Доходности возвращаются к среднему значению (mean reversion)

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

Моменты случайной величины

Серия по доходности финансового актива – случайная величина, которая имеет некоторое распределение. Для того, чтобы лучше описать это распределение, можно оценить его моменты.

Среднее арифметическое (или ожидаемое значение) – определяет центральную тенденцию случайной величины. Для финансовых активов обычно интересен вопрос о том, является ожидаемое значение равным нулю.

Второй момент определяет изменчивость или дисперсию случайной величины. Для финансовых активов среднеквадратическое отклонение (квадратый корень дисперсии) определяет степень риска.

Два первых момента уникальным определяют нормальное распределение. Для других распределелий моменты более высокого порядка могут представлять интерес.

t-критерий Стьюдента

Мы можем использовать t-критерий для проверки гипотезе о равенстве среднего арифметического серии доходностей нулю.

$ H_0: = 0, H_1: 0 $


    One Sample t-test

data:  eurusd.ret
t = 0.23364, df = 5034, p-value = 0.8153
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 -0.0001459491  0.0001854438
sample estimates:
   mean of x 
1.974738e-05

p-value отражает вероятность получения таких наблюдаемых значений теста при условии, что нулевая гипотеза верна. МЕНЬШЕЕ значение p-value означает больше оснований в пользу альтернативной гипотезы ($H1$).

Эксцесс и нормальность доходностей

Эксцесс (kurtosis) – мера “остроты” пика распределения случайной величины.
Эксцесс нормально распределенный величины равен 3. Поэтому обычно в формуле эксцесса вычитают 3 для того, чтобы коэффициент эксцесса нормального распределения был равен нулю. Он положителен, если пик распределения около математического ожидания острый, и отрицателен, если пик очень гладкий.

require(nortest)

Loading required package: nortest


Attaching package: 'nortest'

The following object is masked _by_ '.GlobalEnv':

    ad.test

e1071::kurtosis(data$sp500.ret, na.rm=TRUE) # избыточный эксцесс(excess kurtosis), 0  -- для нормального распределения

[1] 26.74453

nortest::ad.test(data$sp500.ret)


    Anderson-Darling normality test

data:  data$sp500.ret
A = 259.8, p-value < 2.2e-16

qqnorm(data$sp500.ret) # график кванталь-квантиль 
qqline(data$sp500.ret)

Доходности имеют избыточный эксцесс (“тяжелые хвосты” – heavy tails).

Волатильности устойчивы (persistent) во времени

квадраты доходностей

fancy.plot(data$date, (data$sp500.ret)^2, t="l", xlab="Date", ylab="Квадрат доходности", col=2)

mod.vol <- lm(data =data, sp500.ret^2 ~ sp500.ret.lag^2)
cor(data$sp500.ret,data$sp500.ret.lag, use = "complete.obs" )

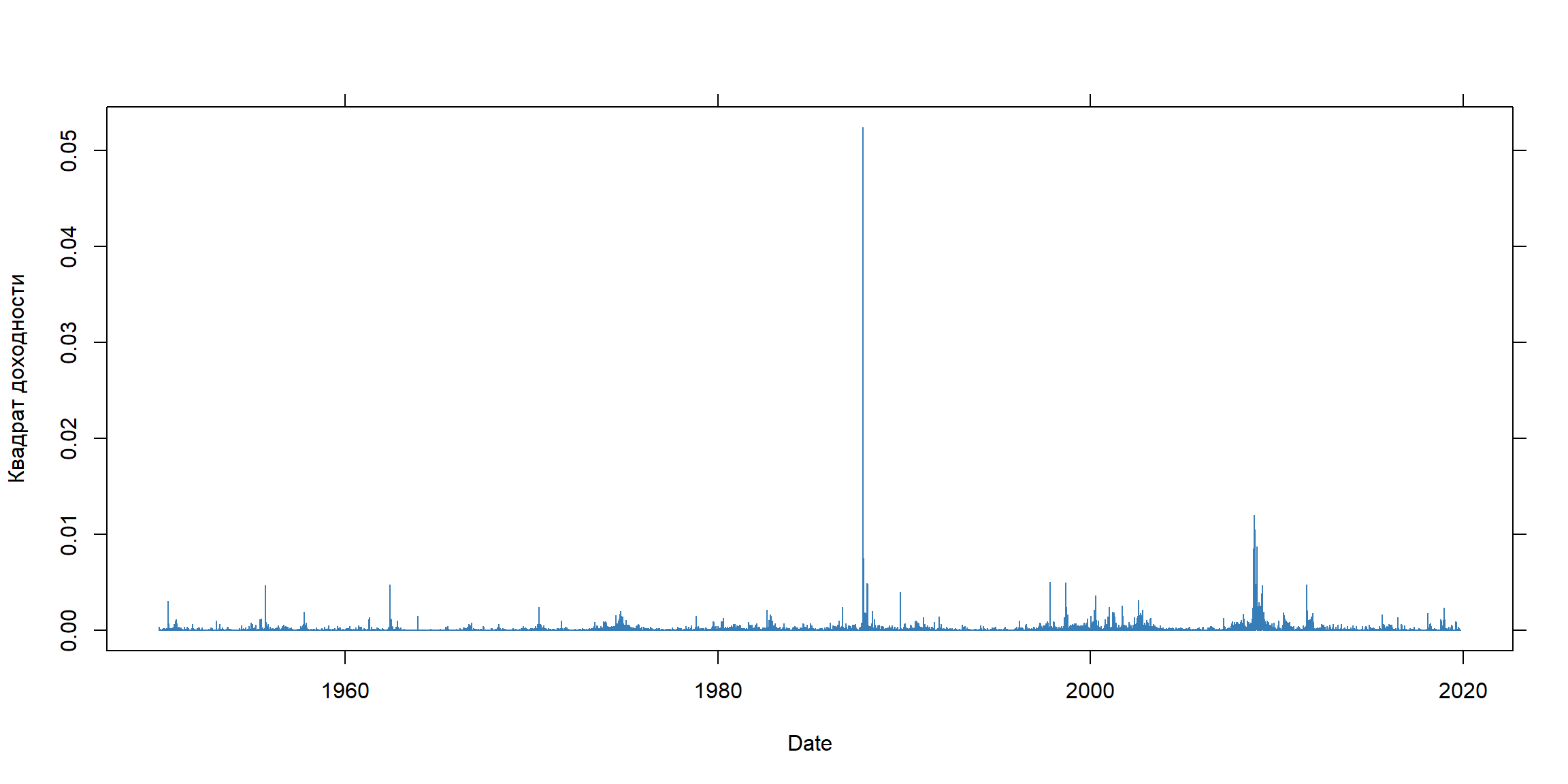
[1] 0.02538831

cor(data$sp500.ret^2,data$sp500.ret.lag^2, use = "complete.obs" )

[1] 0.1451992

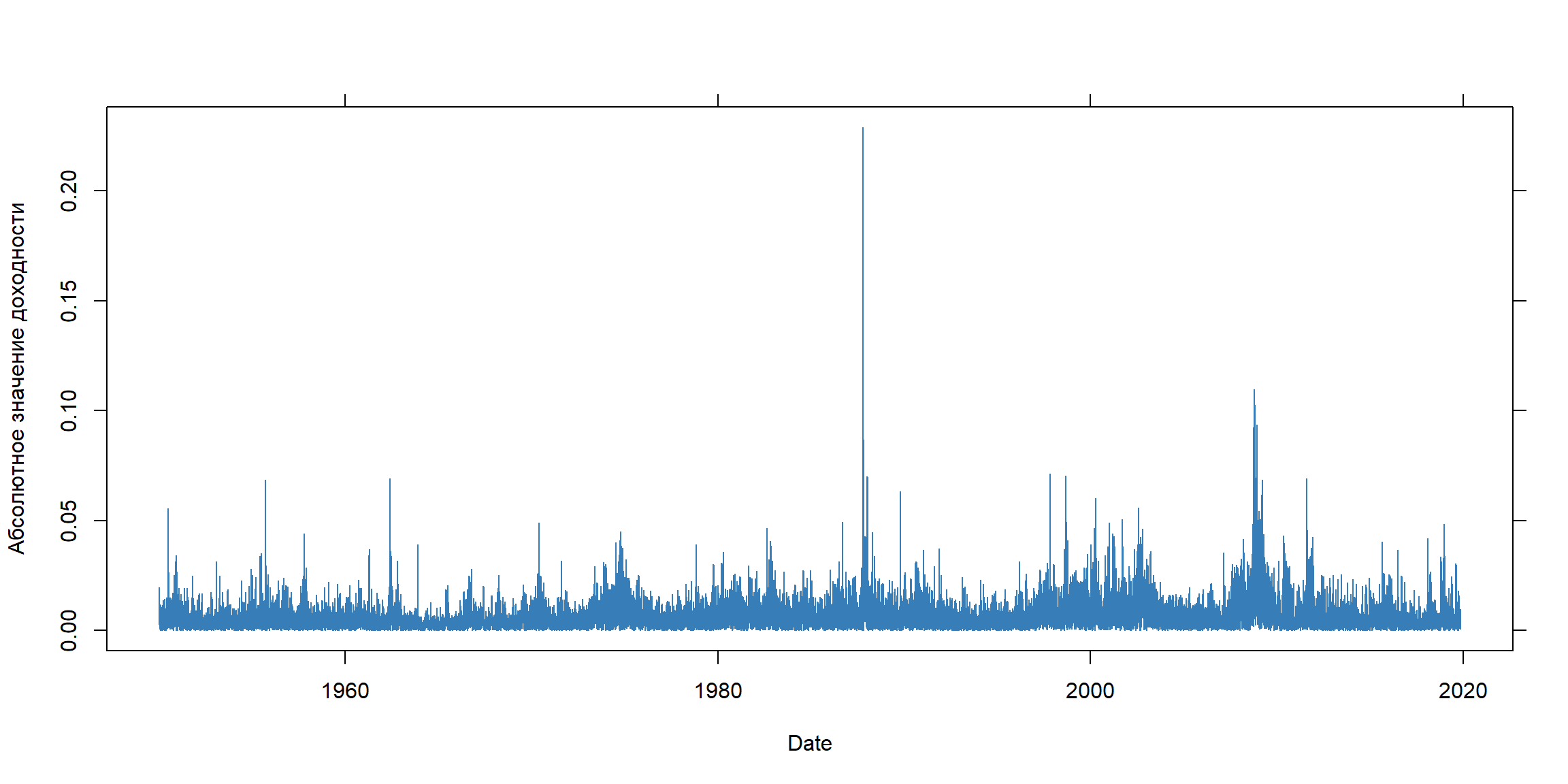
Основные особенности финансовых серий:

Многие финансовые серии растут экспоненциально и имеют изменяющуюся волатильность в зависимости от уровня значений.
Наблюдения, которые находятся рядом, скоррелированны между собой.
Доходности имеют избыточный эксцесс (heavy tails) и не распределены нормально.
Волатильность устойчива во времени (persistent) и часто в финансовых данных наблюдаются кластеры волатильности - периоды большой и низкий волатильности сохраняются определенное время.

Понятие стационарности и почему оно важно

Стандартным допущением при анализе временных рядов является стационарность.
Серия является стационарной, если параметры генерирующего процесса (обычно это среднее и дисперсия) не меняются со временем
Рассмотрим две серии А и B. Параметры серии А (среднее арифметическое, стандартное отклонение) - не меняются со временем

mu = 0
sigma = 1
T = 100
A <- rnorm(T, mu, sigma)
plot(A, type = 'l')

Понятие стационарности и почему оно важно (2)

Для серии B среднее (mean) меняется со временем

mu = 0
sigma = 1
T = 100
B <- rep(0, 100)
t <- seq(0,T, by = 1)

for(i in 1:T){
   B[i] <- rnorm(1, 0.05*i, sigma)
}

plot(B, type = 'l')

Почему не-стационарнасть опасна?

Многие статистические цены требуют, чтобы данные, которые тестируются, были стационарны.

К примеру, возьмем среднее для не-стационарного ряда (серия B, сгенерированная ранее):

Рассчитанное среднее значение для всех точек бессмысленно с точки зрения прогнозирования будущих значений.
Устойчивость параметров во времени дает основания считать, что рассчитанные по прошлым данным параметры, будут иметь значение и в будущем.

Проверим стационарность с помощью стандартного теста

library(tseries)
adf.test(A)

Warning in adf.test(A): p-value smaller than printed p-value


    Augmented Dickey-Fuller Test

data:  A
Dickey-Fuller = -5.1553, Lag order = 4, p-value = 0.01
alternative hypothesis: stationary

adf.test(B)

Warning in adf.test(B): p-value smaller than printed p-value


    Augmented Dickey-Fuller Test

data:  B
Dickey-Fuller = -4.7508, Lag order = 4, p-value = 0.01
alternative hypothesis: stationary

Тесты иногда ошибаются!

Финансовые данные – получение, особенности и трансформация. Количественные финансы

Цели лекции

Финансовые данные

Модель работы с количественными данными

Получение финансовых данных с помощью quantmod и QuantTools

Получение данных из Quandl

Данные Alpha Vantage

Чтение данных из заранее сохраненных файлов

Чтение/запись данных из фойлов Excel

Индекс S&P 500 – долгосрочная динамика фондового рынка

График OHLC

Вариант графика OHLC – bar chart

Внутридневные (intraday) данные

Торговля RUB/USD на прошлой неделе - данные за каждые 15 минут

Преобразование данных – изменение периодичности

Преобразование данных – изменение периодичности

Преобразование данных – первые/последние элементы

Преобразование данных – логарифм

Регрессия логарифма S&P по времени

Может ли вчерашнее значение индекса предсказать нам значение сегодня?

Может ли вчерашнее значение индекса предсказать нам значение сегодня? (2)

Гистограмма лог-значений – проверка допущений

Доходность

Нетто-доходность

Валовая доходность

Лог-доходность (continuously compounded return)

Корректировка на дивиденды для акций

Акции Exxon Mobil - 1

Акции Exxon Mobil - 2

Порядок корректировки цены акции на дивиденды

Полная доходность (total return) для акций Газпрома

Сравнение доходностей нескольких бумаг за период времени

Позволяет ли доходность вчера предсказать доходность сегодня?

Позволяет ли доходность вчера предсказать доходность сегодня? (2)

Гистограмма доходностей – похожа на нормальное распределение?

Моменты случайной величины

t-критерий Стьюдента

Эксцесс и нормальность доходностей

Волатильности устойчивы (persistent) во времени

Основные особенности финансовых серий:

Понятие стационарности и почему оно важно

Понятие стационарности и почему оно важно (2)

Почему не-стационарнасть опасна?

Использованные источники:

Финансовые данные – получение, особенности и трансформация.
Количественные финансы