ARCH/GARCH модели
“Количественные финансы”

Салихов Марсель ()

2020-01-27

Цели лекции

Выводы по ARMA-моделям

Напоминание из прошлой лекции:

Волатильность

Итог: если мы умеем прогнозировать волатильность, то мы можем более аккуратно оценивать стоимость опционов, создавать более продвинутые системы риск-менеджмента и можем создавать стратегии для торговли волатильностью.

Характеристики волатильности

Индекс VIX

require(quantmod)
require(highcharter)
getSymbols('VIXCLS', src = 'FRED')
[1] "VIXCLS"
hchart(VIXCLS)

Волатильность для акций

Пусть мы оцениваем волатильность акций Роснефти. Мы можем оценить волатильность по разным данным: 1) дневная доходность акций за каждый торговый день 2) внутридневная динамика торгов 3) стоимость опционов на акции Роснефти (если они есть). Эти три источника дают три возможных оценки волатильности:

Обычно волатильность сообщается на годовом уровне (% в год). Если вы оценили дневную волатильность, то вы можете оценить годовую волатильность, умножив ее на \(\sqrt{252}\), то есть квадратный корень из количества торговых дней в году (примерно равно 16)

Условная гетероскедастичность (CH)

К примеру, если нестационарный временной ряд имеет выраженную сезонность или устойчивый тренд, то дисперсия ряда изменяется вместе с сезонностью или трендом. Такая регулярность приводит к гетероскедастичности ряда. Почему?

Структура финансового рынка и поведение участников приводит к дополнительным причинам, почему увеличение дисперсии приводит к еще большему увеличению дисперсии в реальной жизни. К примеру, если большое количество участников использует стратегию “защиты” портфеля от снижения стоимости, то падение рынка приводит к автоматическим продажам и росту спросу на инструменты “защиты” (опционы) – то есть, к росту волатильности. Пример - октябрь 1987 года.

Условное (conditional) среднее и дисперсия

Пусть есть страционарная серия доходности \(r_t\), тогда

Ту же самую логику можно использовать для волатильности:

Идентификация условной гетероскедастичности

plot.xts(MICEX.rtn, type = 'l',main  = 'Доходность индекса ММВБ')

t.test(MICEX.rtn) # тестируем среднее доходнстей

    One Sample t-test

data:  MICEX.rtn
t = 1.5861, df = 2021, p-value = 0.1129
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 -9.087398e-05  8.595139e-04
sample estimates:
   mean of x 
0.0003843199

Cудя по t-тесту, мы принимаем гипотезу о том, что среднее доходности равно 0.

AutoRegressive Conditional Heteroskedastic (ARCH) модель

Это и есть базовый принцип ARCH.

Пусть временной ряд \({\epsilon_t}\) имеет следующий вид:

\[ \epsilon_t = \sigma_t w_t \] где \(w_t\) – белый шум с нулевым средним и единичной дисперсией (белый шум может иметь нормальное распределение, но это не обязательно, распределение может быть и иным).

Часть \(\sigma_t\) – условная дисперсия (conditional variance), она имеет вид:

\[\sigma_t^2 = a_0 + a_1 \epsilon_{t-1}^2 \] \(a_0\) и \(a_1\) – это параметры модели, которые необходимо оценить.

Условная дисперсия ряда по определению равно \(\sigma_t^2 = Var(\epsilon_t | e_{t-1}, \ldots)\) ;

В этом случае ряд \({\epsilon_t}\) является процессом ARCH(1). Можно записать модель в следующем виде:

\[\epsilon_t = w_t \sqrt{a_0 + a_1 \epsilon_{t-1}^2} \] \(a_0 >0\) и \(a_1 > 0\) для того, чтобы часть под корнем была больше 0.

\(a_0 + a_1<1\) для того, чтобы ряд оставался стационарным с конечной дисперсией.

Почему ARCH моделирует волатильность?

Немного математики:

\[ Var(\epsilon_t) = E[\epsilon_t^2] - (E[\epsilon_t])^2 = E[\epsilon_t^2] =E[w_t^2]E[a_0 + a_1 \epsilon_{t-1}^2]= \] \[=E[a_0 + a_1 \epsilon_{t-1}^2] = a_0 + a_1 Var(\epsilon_{t-1}) = a_0 + a_1 \epsilon_{t-1}^2 \]

учитывая, что среднее \(w_t\) равно 0, дисперсия – 1, а \(E[\epsilon_t] = 0\)

Когда можно использовать ARCH?

Достоинства и недостатки ARCH

Достоинства:

  1. Модель может “создавать” кластеры волатильности
  2. Модель может “создавать” heavy tails

Недостатки:

  1. Модель трактует положительные и отрицательные шоки одинаковым образом с точки зрения влияния на волатильность. Эмпирические наблюдения и здравый смысл говорят, что эти шоки различны.
  2. Модель ARCH накладывает достаточно сильные ограничения на значения коэффициентов модели. Это ограничивает возможности моделировать более высокие моменты (к примеру, избыточный эксцесс).
  3. Модель ARCH не дает возможность оценки источников шоков, это просто механистический способ оценки поведения условной дисперсии.
  4. Модель ARCH недооценивает волатильность, так как достаточно медленно реагирует на большие по значению шоки.
  5. Модель на фактических требует достаточно большого количество параметров для оценки, что увеличивает вероятность overfitting.

ARCH(p)

Модель ARCH порядка \(p\) имеет следующий вид:

\[\sigma_t^2 = w_t \sqrt{a_0 + \sum_{i=1}^{p} a_i \epsilon_{t-i}^2} \]

Тестирование ARCH-эффекта

Пусть уравнение для среднего выглядит следующим образом: \(a_t = r + \mu_t\). Мы можем использовать квадраты остатков (\(a_t^2\)), чтобы проверить серию на условную гетерокседастичность (ARCH-эффект). Есть два варианта тестирования ARCH-эффекта:

  1. Использовать тест Льюнга-Бокса (Ljung-Box test) для серии \(\{a_t^2\}\) – мы проходили этот тест в ARMA-моделях
  2. Использовать тест множителей Лагранжа (см. Engle (1982)). Этот тест эквивалентен обычному F-тесту на тестирование гипотезы (\(\alpha_i = 0\)) в уравнении:

\[ a_t^2 = \alpha _0 + \alpha_1 a_{t-1}^2 +\ldots + \alpha_{t-m}^2 + \epsilon_t, t = m +1, ..., T \]

Проверка ARCH-эффекта для доходностей индекса ММВБ

require(FinTS)
Loading required package: FinTS

Attaching package: 'FinTS'
The following object is masked from 'package:forecast':

    Acf
y <- MICEX.rtn - mean(MICEX.rtn)
Box.test(y^2,lag = 10,type = 'Ljung')

    Box-Ljung test

data:  y^2
X-squared = 99.046, df = 10, p-value < 2.2e-16
ArchTest(y,12) 

    ARCH LM-test; Null hypothesis: no ARCH effects

data:  y
Chi-squared = 78.243, df = 12, p-value = 8.919e-12

Оба теста указывают на присутствие ARCH-эффекта в серии

Определение порядка ARCH модели

Pacf(y^2)

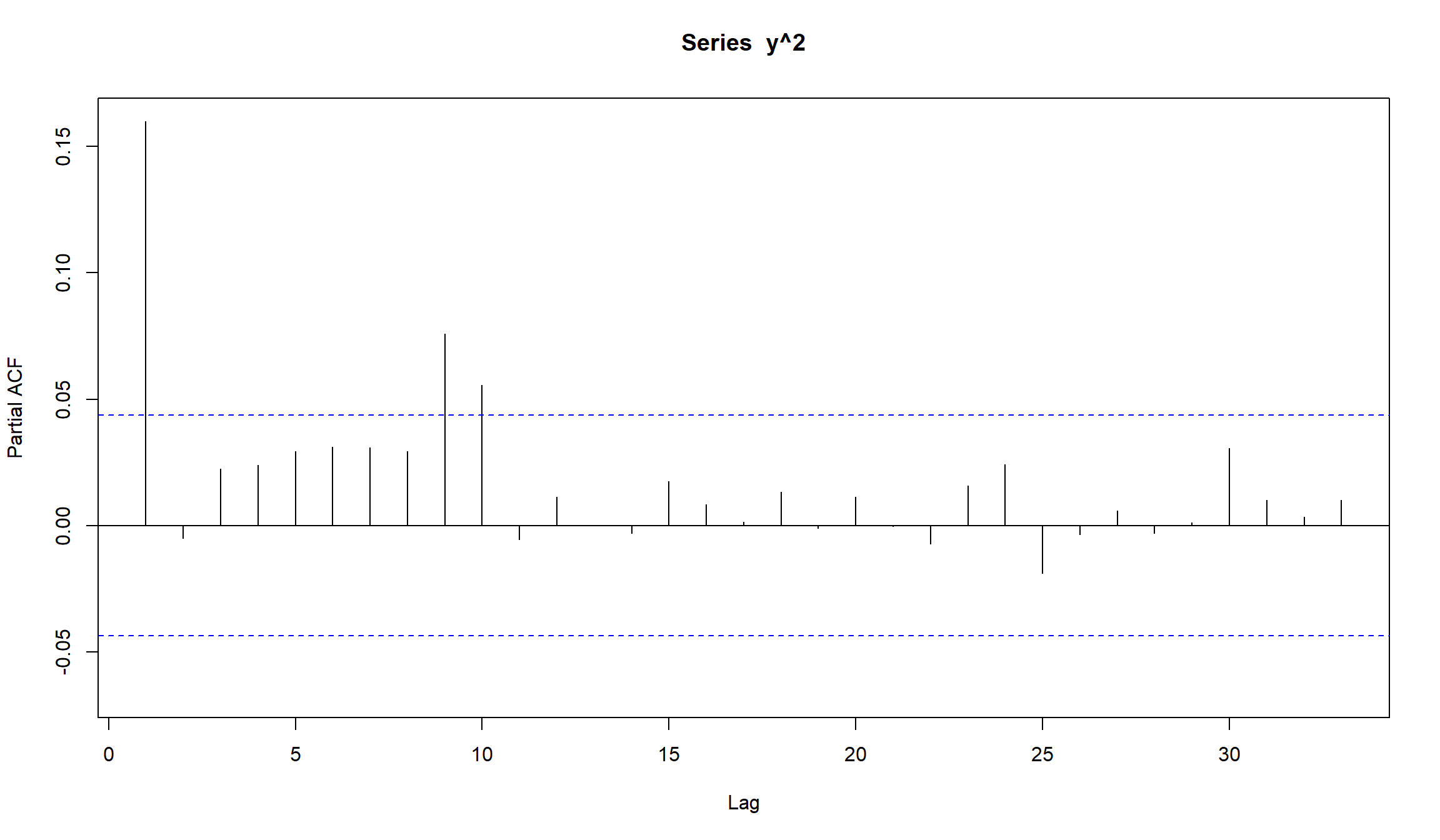
Можем оценить ARMA(1,1) модель для среднего доходностей и посмотреть на квадраты остатков этой модели:

arma11 <- Arima(MICEX.rtn, order=c(1, 0, 1))
Pacf(resid(arma11)^2)

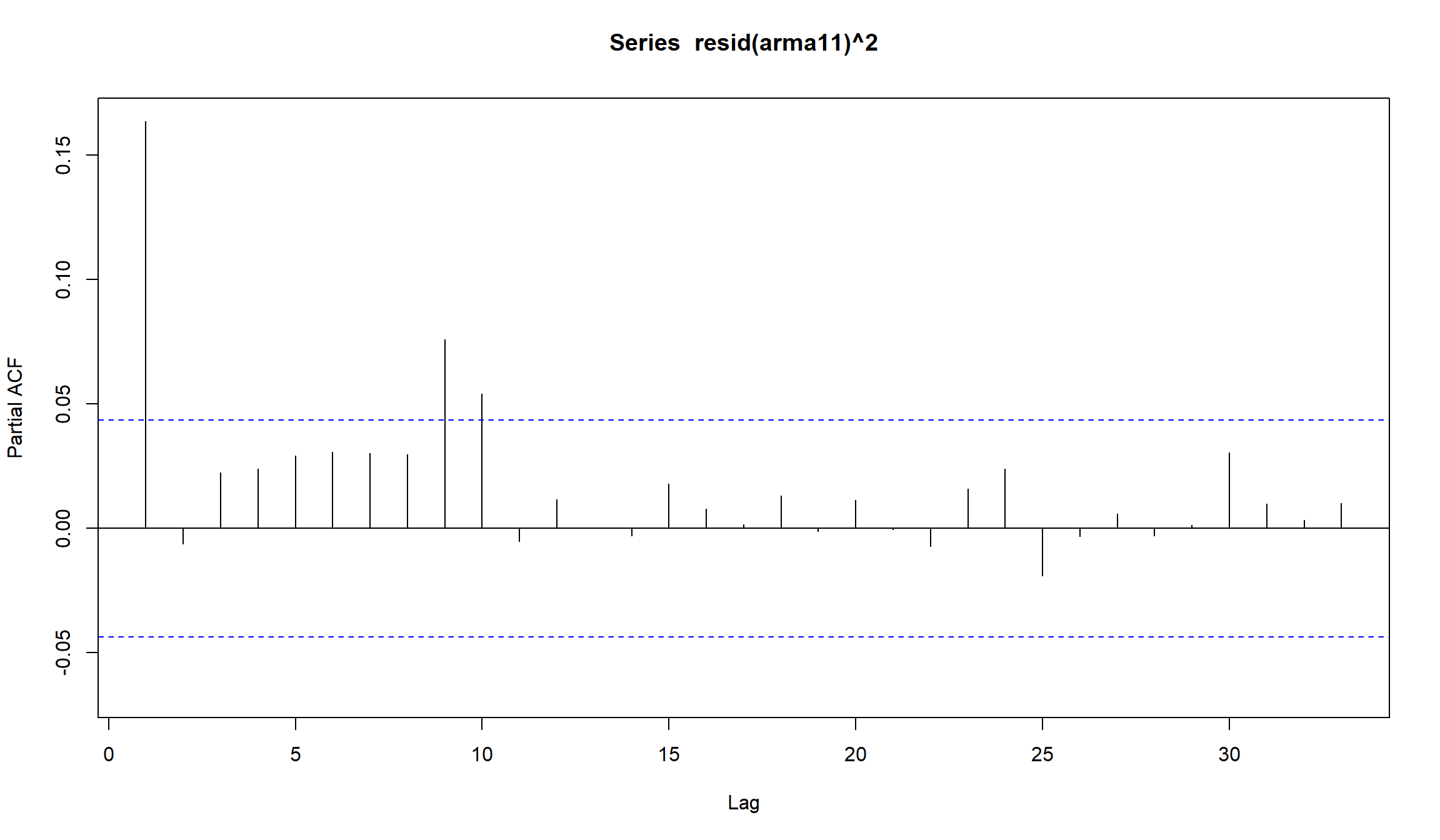
Как видно, требуется достаточно много лагов (порядок модели), чтобы использовать ARCH.

Симулирование AR(1) + ARCH(1)

AR(1) модель для среднего и ARCH(1) для дисперсии можно симулировать следующим образом:

n = 10200 #
e = rnorm(n)
a = e # ARCH
y = e # AR + ARCH
sig2 = e^2 # условная дисперсия
# параметры для ARCH
omega = 1
alpha = 0.55
#параметры для AR
phi = 0.8
mu = 0.1
omega/(1-alpha) # безусловное ст. отклонение
[1] 2.222222
sqrt(omega/(1-alpha))
[1] 1.490712
set.seed("1234")
for (t in 2:n)
{
  a[t] = sqrt(sig2[t])*e[t]
  y[t] = mu + phi*(y[t-1]-mu) + a[t] # моделирование AR
  sig2[t+1] = omega + alpha * a[t]^2 # моделирование ARCH
}

par(mfrow=c(2,4))
plot(e[10001:n],type="l",xlab="t",ylab=expression(epsilon),main="(a) белый шум")
plot(sqrt(sig2[10001:n]),type="l",xlab="t",ylab=expression(sigma[t]),
     main="(b) условная дисперсия")
plot(a[10001:n],type="l",xlab="t",ylab="a",main="(c) ARCH")
plot(y[10001:n],type="l",xlab="t",ylab="y",main="(d) AR+ARCH")
acf(a[10001:n],main="(e) ARCH")
acf(a[10001:n]^2,main="(f) ARCH squared")
acf(y[10001:n],main="(g) AR+ARCH")
acf(y[10001:n]^2,main="(h) AR+ARCH squared")

par(mfrow=c(1,1))

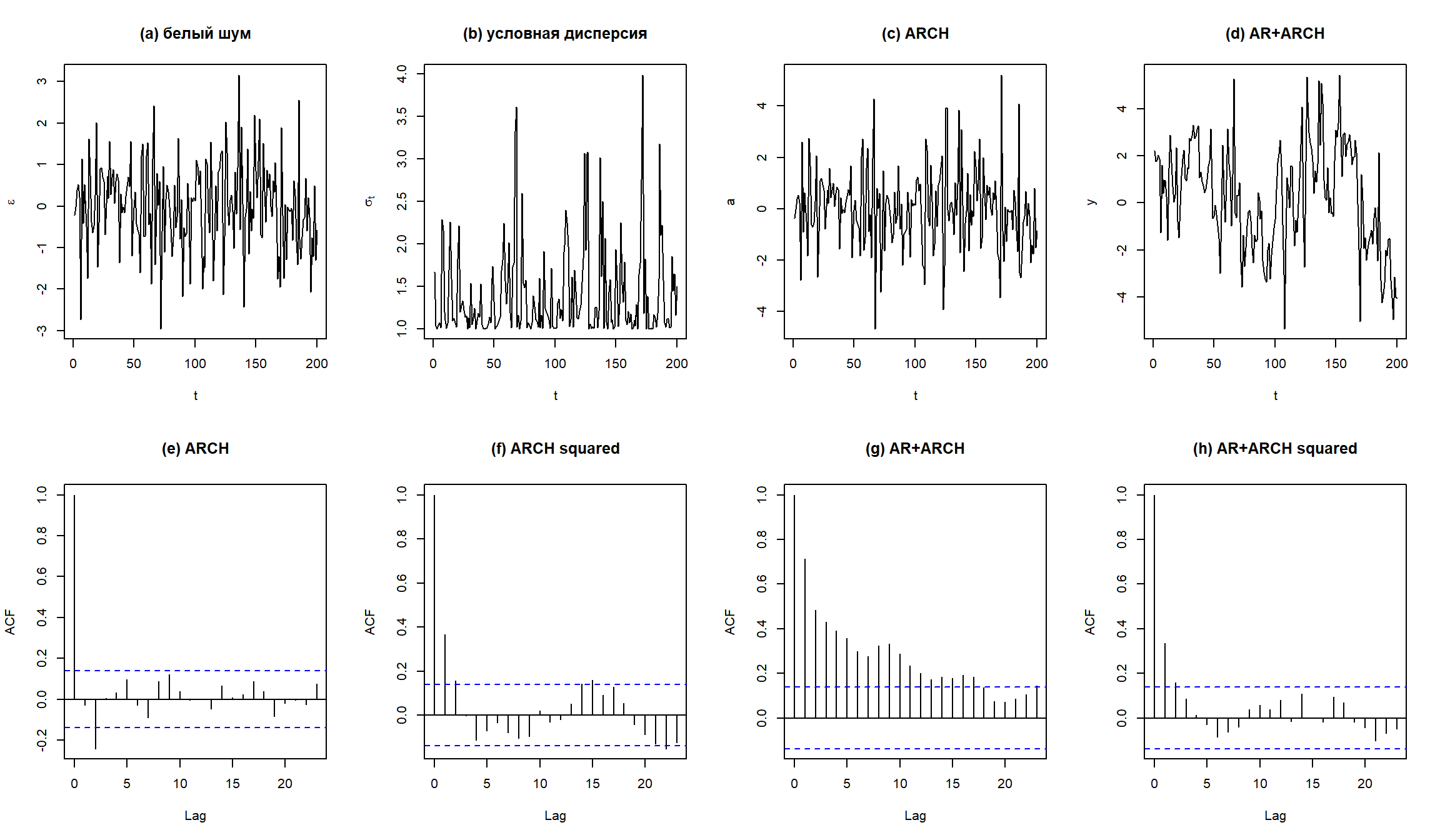
Оценка ARCH-модели

Оценим ARCH(1)-модель для доходностей ММВБ при допущении о том, что среднее доходностей является константой. Используем помощью функцию garchFit из пакета fGarch.

library(fGarch)
arch1 <- garchFit(~1+garch(1,0),data=MICEX.rtn,trace=F)
summary(arch1)

Title:
 GARCH Modelling 

Call:
 garchFit(formula = ~1 + garch(1, 0), data = MICEX.rtn, trace = F) 

Mean and Variance Equation:
 data ~ 1 + garch(1, 0)
<environment: 0x0000000018ece1a8>
 [data = MICEX.rtn]

Conditional Distribution:
 norm 

Coefficient(s):
        mu       omega      alpha1  
0.00038083  0.00010574  0.10391464  

Std. Errors:
 based on Hessian 

Error Analysis:
        Estimate  Std. Error  t value Pr(>|t|)    
mu     3.808e-04   2.385e-04    1.597 0.110311    
omega  1.057e-04   4.056e-06   26.068  < 2e-16 ***
alpha1 1.039e-01   2.689e-02    3.865 0.000111 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Log Likelihood:
 6293.094    normalized:  3.112312 

Description:
 Mon Jan 27 19:09:49 2020 by user: m_salihov 


Standardised Residuals Tests:
                                Statistic p-Value   
 Jarque-Bera Test   R    Chi^2  9244.496  0         
 Shapiro-Wilk Test  R    W      0.9469179 0         
 Ljung-Box Test     R    Q(10)  6.961889  0.7290379 
 Ljung-Box Test     R    Q(15)  10.07718  0.8148569 
 Ljung-Box Test     R    Q(20)  13.19756  0.8687475 
 Ljung-Box Test     R^2  Q(10)  20.55691  0.0244041 
 Ljung-Box Test     R^2  Q(15)  22.82345  0.08796106
 Ljung-Box Test     R^2  Q(20)  25.45383  0.1846171 
 LM Arch Test       R    TR^2   18.61699  0.09820034

Information Criterion Statistics:
      AIC       BIC       SIC      HQIC 
-6.221656 -6.213330 -6.221661 -6.218601 
res  <- residuals(arch1,standardize=T) # используем стандартизированные остатки для диагностики модели 
Acf(res,lag=20)

Pacf(res,lag=20)

# plot(arch1) диагностические графики для модели 
plot(arch1, which = 13) # QQ-Plot of Standardized Residuals

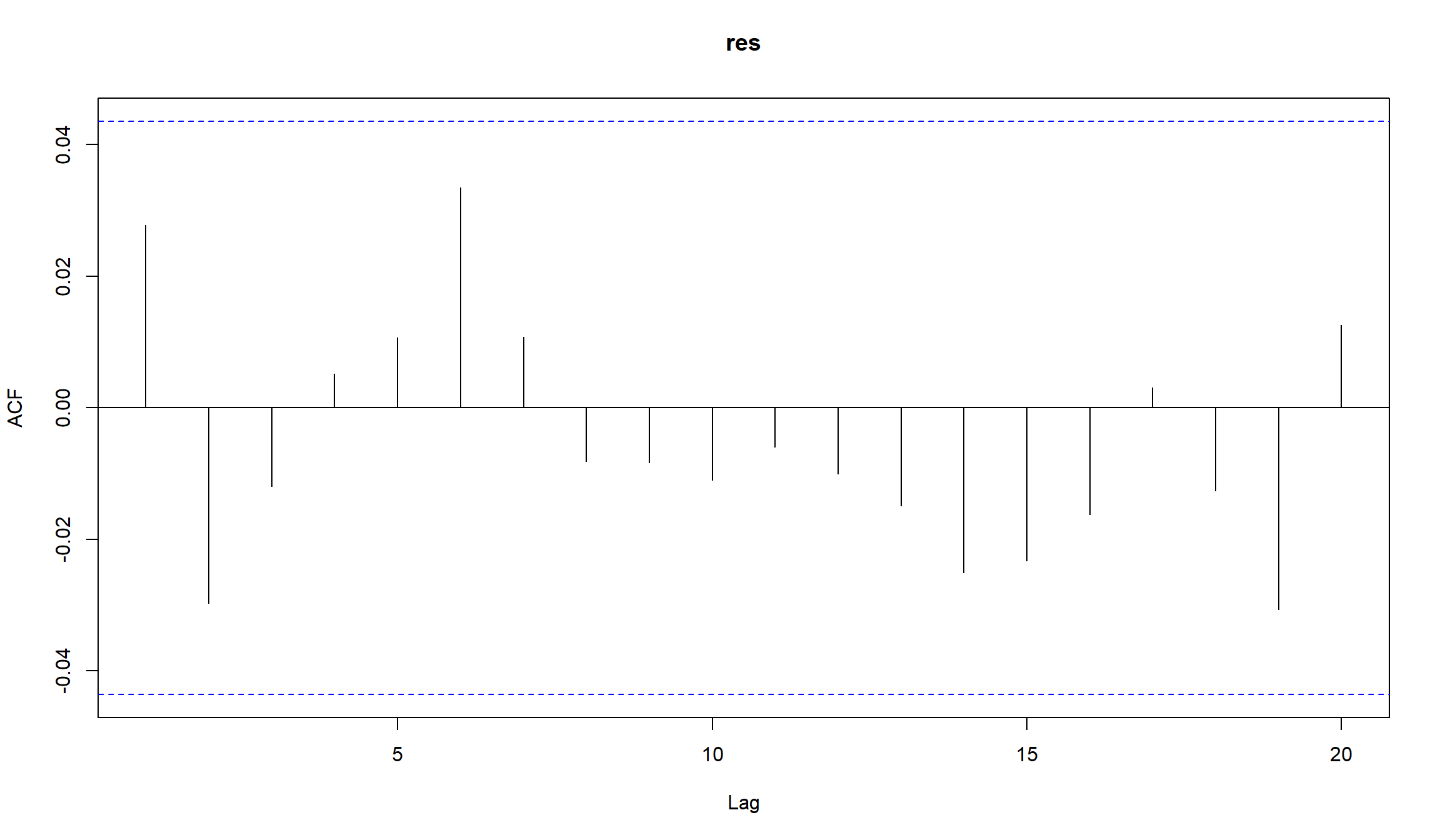
Оцененная модель имеет вид:

\[ r_t = 0.00024345 + a_t, \sigma^2 = 0.00011673 + 0.09224500 a_{t-1}^2 \] Все коэффициенты являются значимыми. ACF и PACF указывают на отсутствие автокорреляции в остатках

Оценка ARCH(1) c распределением Стьюдента для шоков

Та же самая модель с t-распределением Стьюдента для моделирования шоков серии.

arch1_student <- garchFit(~1+garch(1,0),data=MICEX.rtn,trace=F, cond.dist="std")
summary(arch1_student)

Title:
 GARCH Modelling 

Call:
 garchFit(formula = ~1 + garch(1, 0), data = MICEX.rtn, cond.dist = "std", 
    trace = F) 

Mean and Variance Equation:
 data ~ 1 + garch(1, 0)
<environment: 0x000000001bd17fc8>
 [data = MICEX.rtn]

Conditional Distribution:
 std 

Coefficient(s):
        mu       omega      alpha1       shape  
4.6079e-04  9.7941e-05  1.3503e-01  5.8797e+00  

Std. Errors:
 based on Hessian 

Error Analysis:
        Estimate  Std. Error  t value Pr(>|t|)    
mu     4.608e-04   2.138e-04    2.155 0.031167 *  
omega  9.794e-05   5.550e-06   17.647  < 2e-16 ***
alpha1 1.350e-01   3.644e-02    3.705 0.000211 ***
shape  5.880e+00   7.148e-01    8.226 2.22e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Log Likelihood:
 6403.433    normalized:  3.166881 

Description:
 Mon Jan 27 19:09:49 2020 by user: m_salihov 


Standardised Residuals Tests:
                                Statistic p-Value   
 Jarque-Bera Test   R    Chi^2  10009.05  0         
 Shapiro-Wilk Test  R    W      0.9455571 0         
 Ljung-Box Test     R    Q(10)  6.67251   0.7559579 
 Ljung-Box Test     R    Q(15)  9.778589  0.8334312 
 Ljung-Box Test     R    Q(20)  12.76429  0.8872668 
 Ljung-Box Test     R^2  Q(10)  17.39947  0.06597898
 Ljung-Box Test     R^2  Q(15)  19.40363  0.1960224 
 Ljung-Box Test     R^2  Q(20)  21.53908  0.3660359 
 LM Arch Test       R    TR^2   16.2183   0.1814409 

Information Criterion Statistics:
      AIC       BIC       SIC      HQIC 
-6.329805 -6.318703 -6.329813 -6.325731 
res  <- residuals(arch1_student,standardize=T) # используем стандартизированные остатки
Acf(res,lag=20)

Pacf(res,lag=20)

plot(arch1_student, which = 13) # QQ-Plot of Standardized Residuals

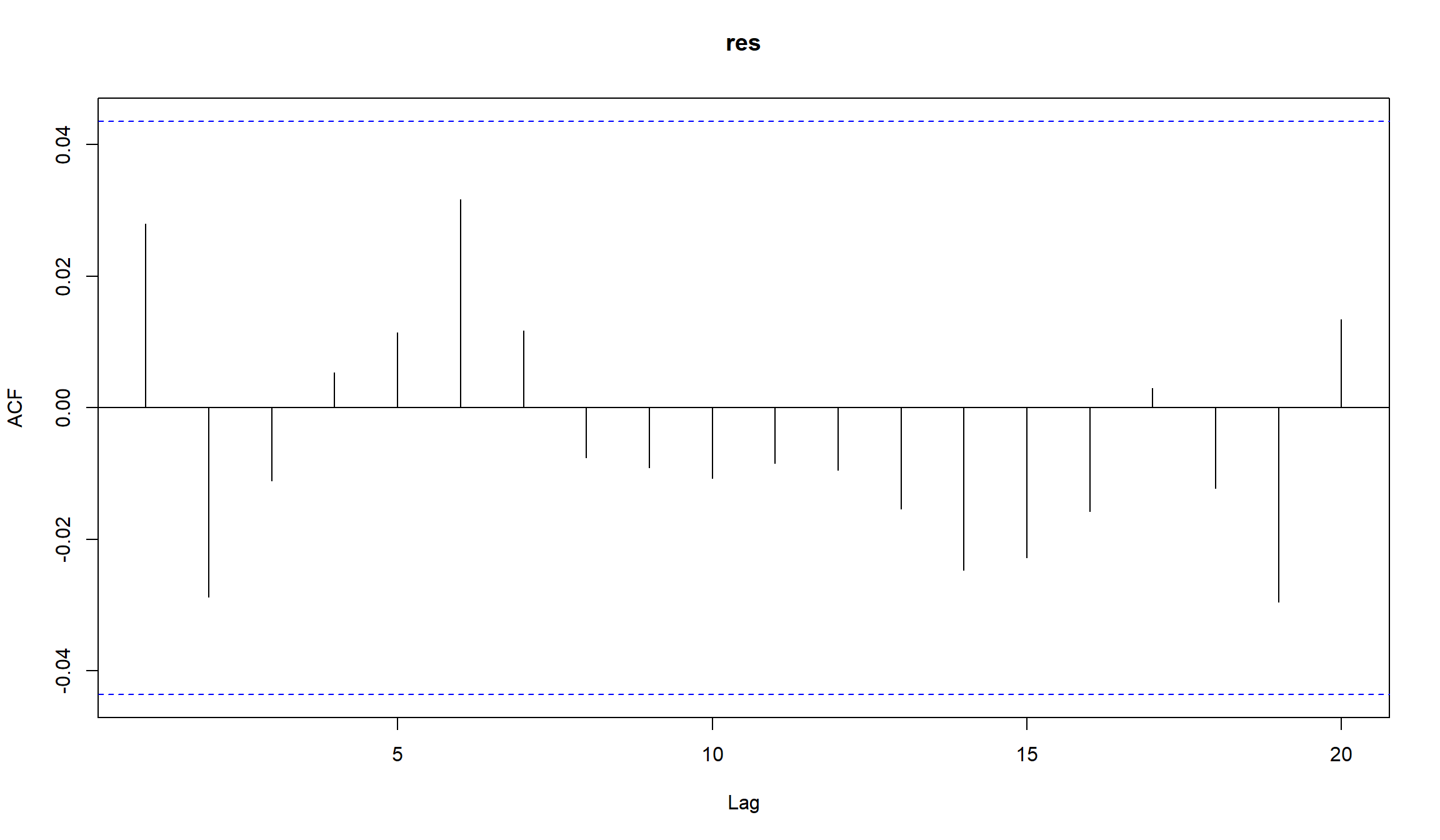
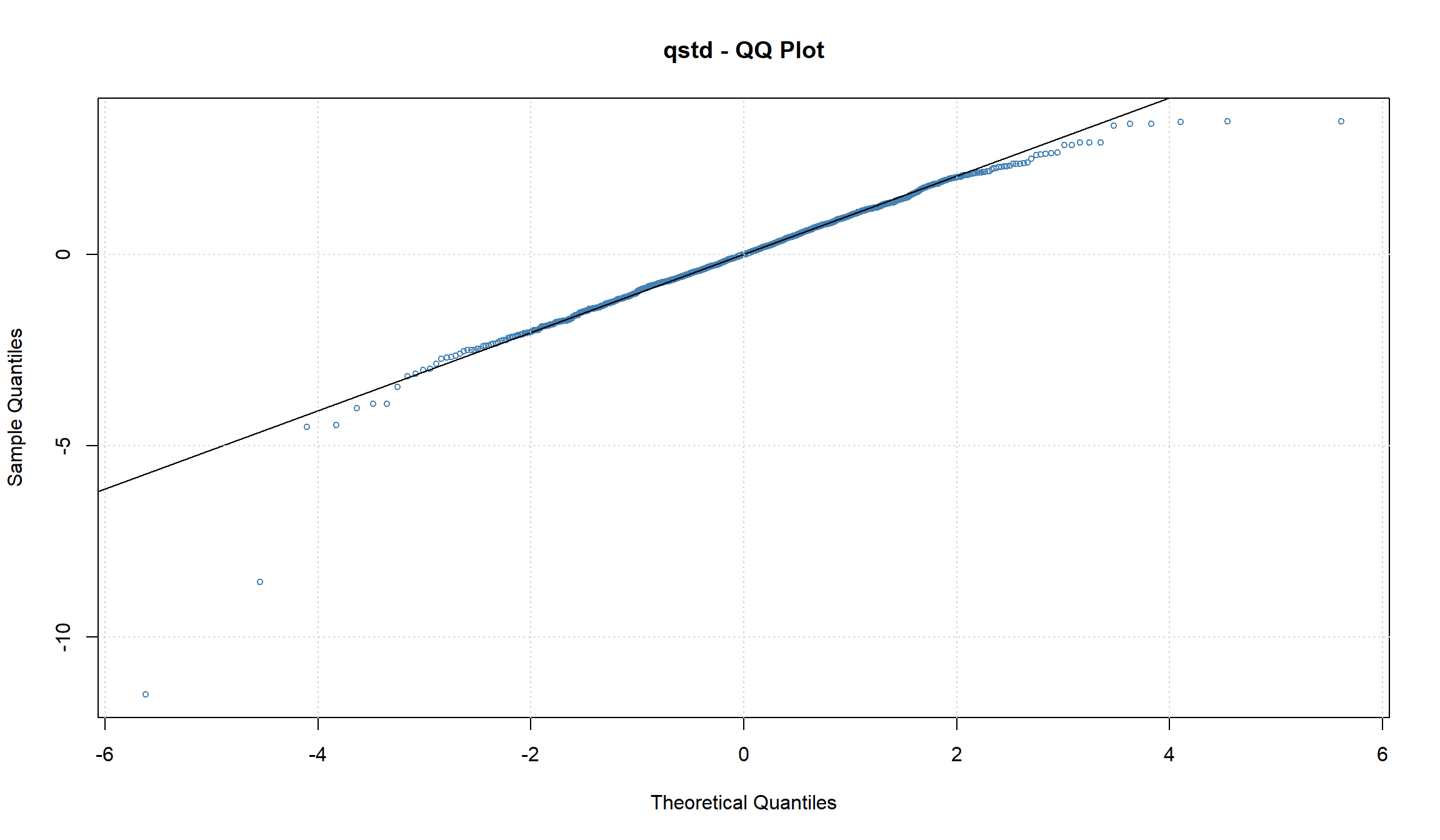
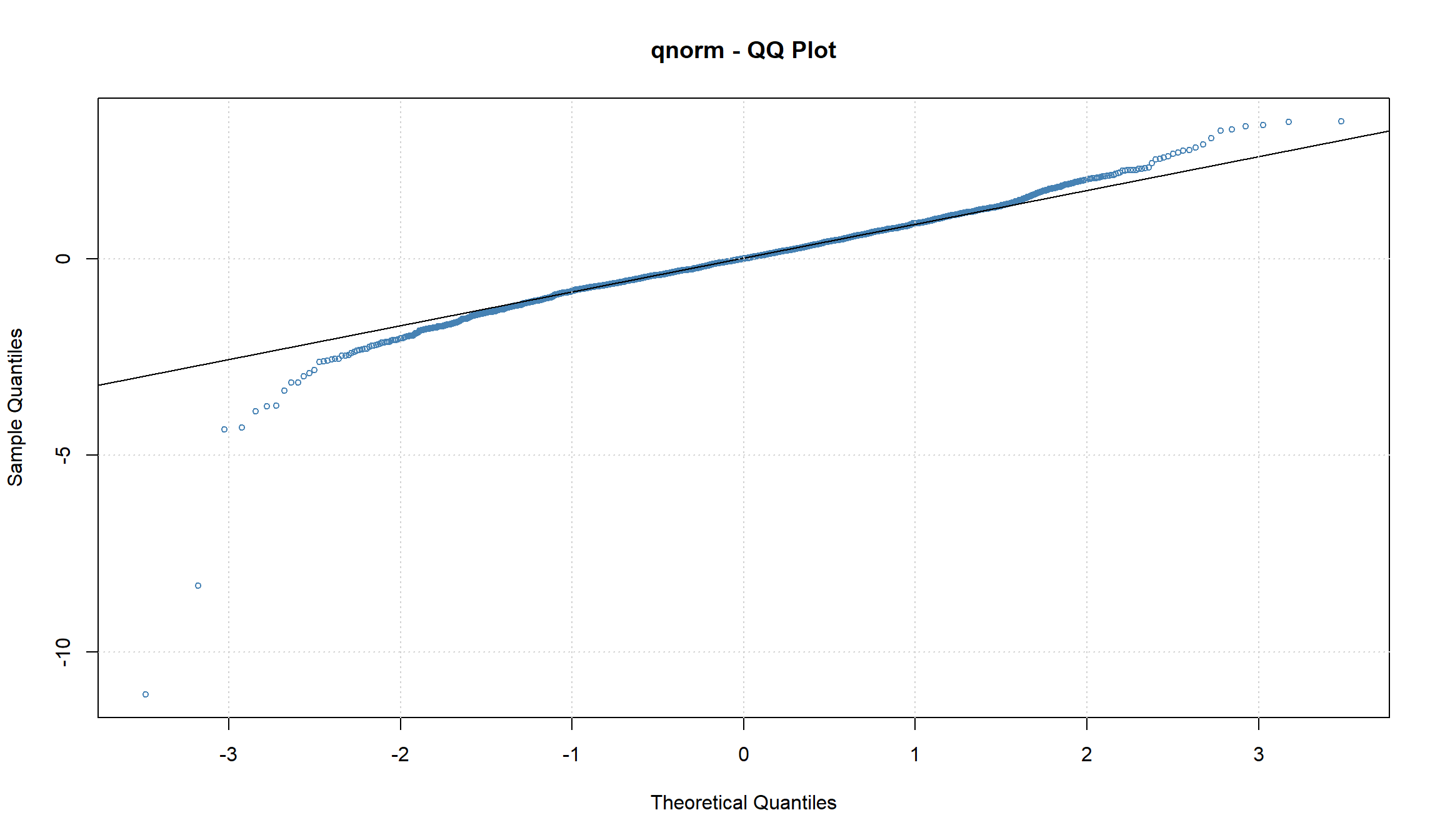
Использование распределения с более “тяжелыми хвостами” несколько уменьшило значение ARCH-коэффициента. График квантиль-квантиль также подтверждает, что использование распределения Стьюдента для шоков, приводит к более “нормальным” остаткам модели

Определение GARCH

Временной ряд \({\epsilon_t}\) имеет следующий вид:

\[ \epsilon_t = \sigma_t w_t \]

где \(w_t\) – белый шум с нулевым средним и единичной дисперсией, а часть \(\sigma_t^2\) имеет вид:

\[\sigma_t^2 = a_0 +\sum_{i=1}^{q} a_i \epsilon_{t-i}^2+ \sum_{j=1}^{p} \beta_i \sigma_{t-j}^2 \]

где \(\alpha_i\) и \(\beta_j\) – это параметры модели. Процесс \(\epsilon_t\) является GARCH(p,q)

Симулирование GARCH(1,1)

GARCH(1,1) будет иметь следующий вид:

\[\epsilon_t = \sigma_t w_t \] \[ \sigma_t^2 = a_0 + a_1 \epsilon_{t-1}^2 + \beta_1 \sigma_{t-1}^2 \]

set.seed(2)
# параметры модели 
a0 <- 0.2
a1 <- 0.5
b1 <- 0.3
w <- rnorm(10000) ## белый шум
eps <- rep(0, 10000) ## исходный ряд, пока заполненный нулями 
sigsq <- rep(0, 10000) ## компонента GARCH

for (i in 2:10000) {
   sigsq[i] <- a0 + a1 * (eps[i-1]^2) + b1 * sigsq[i-1]
   eps[i] <- w[i]*sqrt(sigsq[i])
}

plot(eps, type = 'l')

Acf(eps)

вроде бы ничего необычного. Но если мы построим корелограмму квадратов рядов, то увидим выраженное убывание на последующих лагах (характеристика AR-процесса)

Acf(eps^2)

Pacf(eps^2)

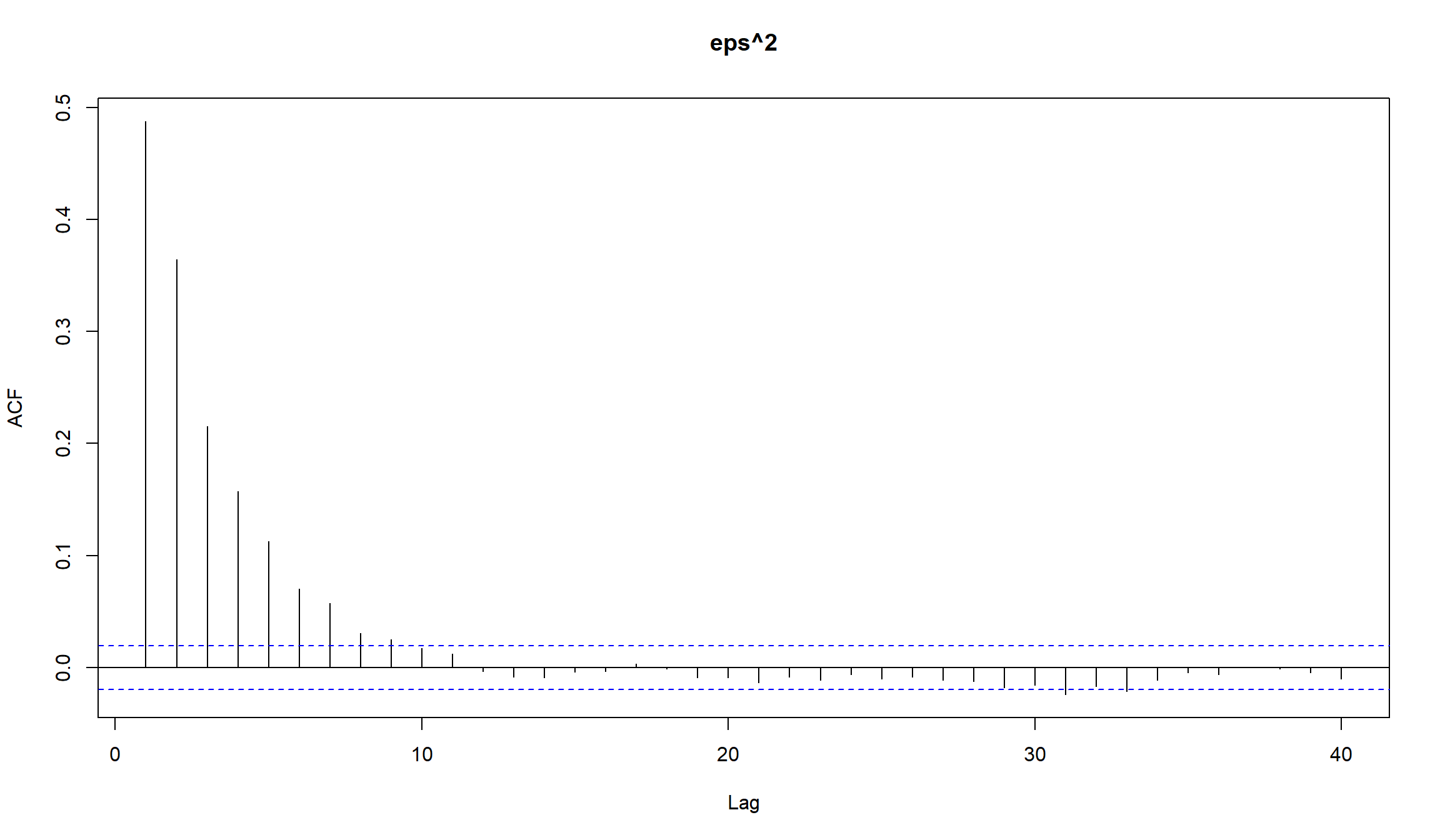
Оценка симулированной GARCH(1,1)-модели

Мы можем также использовать функцию garch из пакета tseries

library(tseries)
eps.garch <- garch(eps, trace=FALSE)
summary(eps.garch)

Call:
garch(x = eps, trace = FALSE)

Model:
GARCH(1,1)

Residuals:
     Min       1Q   Median       3Q      Max 
-4.11672 -0.66558  0.01997  0.68409  3.53687 

Coefficient(s):
    Estimate  Std. Error  t value Pr(>|t|)    
a0  0.197947    0.009858    20.08   <2e-16 ***
a1  0.465840    0.019720    23.62   <2e-16 ***
b1  0.323213    0.018907    17.09   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Diagnostic Tests:
    Jarque Bera Test

data:  Residuals
X-squared = 0.40598, df = 2, p-value = 0.8163


    Box-Ljung test

data:  Squared.Residuals
X-squared = 0.49885, df = 1, p-value = 0.48
confint(eps.garch)
       2.5 %    97.5 %
a0 0.1786255 0.2172683
a1 0.4271900 0.5044903
b1 0.2861566 0.3602687

Оценка GARCH(1,1) для индекса ММВБ

Оценим GARCH(1,1) при допущении о том, что среднее доходностей является константой:

library(fGarch)
garch11 <- fGarch::garchFit(~1+garch(1,1),data = MICEX.rtn,trace=F) # часть ~1 говорит о том, что надо оценивать константу
summary(garch11)

Title:
 GARCH Modelling 

Call:
 fGarch::garchFit(formula = ~1 + garch(1, 1), data = MICEX.rtn, 
    trace = F) 

Mean and Variance Equation:
 data ~ 1 + garch(1, 1)
<environment: 0x0000000017337ee0>
 [data = MICEX.rtn]

Conditional Distribution:
 norm 

Coefficient(s):
        mu       omega      alpha1       beta1  
5.9404e-04  4.6072e-06  5.6942e-02  9.0595e-01  

Std. Errors:
 based on Hessian 

Error Analysis:
        Estimate  Std. Error  t value Pr(>|t|)    
mu     5.940e-04   2.264e-04    2.624 0.008702 ** 
omega  4.607e-06   1.346e-06    3.424 0.000618 ***
alpha1 5.694e-02   1.320e-02    4.314  1.6e-05 ***
beta1  9.060e-01   2.072e-02   43.724  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Log Likelihood:
 6344.531    normalized:  3.13775 

Description:
 Tue Jan 28 20:27:35 2020 by user: m_salihov 


Standardised Residuals Tests:
                                Statistic p-Value  
 Jarque-Bera Test   R    Chi^2  18025.48  0        
 Shapiro-Wilk Test  R    W      0.938596  0        
 Ljung-Box Test     R    Q(10)  3.038938  0.9804928
 Ljung-Box Test     R    Q(15)  5.947652  0.9806137
 Ljung-Box Test     R    Q(20)  8.487828  0.9881163
 Ljung-Box Test     R^2  Q(10)  0.9285449 0.9998776
 Ljung-Box Test     R^2  Q(15)  1.423367  0.999997 
 Ljung-Box Test     R^2  Q(20)  1.756941  1        
 LM Arch Test       R    TR^2   1.110188  0.9999747

Information Criterion Statistics:
      AIC       BIC       SIC      HQIC 
-6.271544 -6.260443 -6.271552 -6.267470 
coef(garch11)
          mu        omega       alpha1        beta1 
5.940427e-04 4.607179e-06 5.694173e-02 9.059504e-01 
v11 = garch11@sigma.t*sqrt(252)*100
plot(index(MICEX.rtn), v11,type='l', xlab= 'год',ylab='% год', main = 'Оценка волатильности индекса ММВБ на основе GARCH(1,1) модели')

Мы можем также использовать критерии AIC/BIC для выбора лучшей GARCH модели

Варианты для моделей доходностей

Мы используем только одну серию для моделирования – серию фактических доходностей. Модель GARCH раскладывает эту серию на три части:

  1. Среднее арифметическое доходности в момент \(t\)
  2. Условная дисперсия в момент времени \(t\)
  3. Шок в момент времени \(t\).

Мы можем использовать разные подходы для оценки среднего доходностей (часть 1):

Спецификация модели GARCH позволяется определить каким образом, рассчитываются части 2 и 3.

Оценка GARCH(1,1) с ARMA-моделью

fit_best <- auto.arima(MICEX.rtn)
summary(fit_best)
Series: MICEX.rtn 
ARIMA(2,0,2) with non-zero mean 

Coefficients:
         ar1      ar2      ma1     ma2   mean
      0.7792  -0.5664  -0.7773  0.5322  4e-04
s.e.  0.5145   0.5738   0.5211  0.5885  2e-04

sigma^2 estimated as 0.0001187:  log likelihood=6271.65
AIC=-12531.3   AICc=-12531.26   BIC=-12497.63

Training set error measures:
                        ME       RMSE         MAE  MPE MAPE      MASE
Training set -4.443801e-05 0.01088199 0.007951956 -Inf  Inf 0.7091144
                    ACF1
Training set 0.003324274
garch_best <- garchFit(~ arma(3,3)+ garch(1,1), data=MICEX.rtn,
                         trace = F, include.mean = TRUE)

Предупреждение указывает на то, что оптимизатор не смог найти значения коэффициентов. Поэтому текущие значения коэффициентов не имеют большого смысла.

Оценка GARCH(1,1) + ARMA(3,3) для доходностей индекса ММВБ с помощью rugarch

попробуем использовать пакет rugarch. В этом пакете сначала необходимо создать объект, определяющиий тип оцениваемой модели, с помощью функции ugarchspec. Функция ugarchfit уже оценивает непосредственно модель. Для сложных моделей оценка может занимать определенное время.

library(rugarch)
spec = ugarchspec(
                 variance.model=list(garchOrder=c(1,1)),
                 mean.model=list(armaOrder=c(3,3), include.mean=T),
                 distribution.model="sged")

fit = tryCatch(
       ugarchfit
       (
         spec, 
         MICEX.rtn, 
         solver = 'hybrid'
       ), 
       error=function(e) e, 
       warning=function(w) w
     )
(fit)

*---------------------------------*
*          GARCH Model Fit        *
*---------------------------------*

Conditional Variance Dynamics   
-----------------------------------
GARCH Model : sGARCH(1,1)
Mean Model  : ARFIMA(3,0,3)
Distribution    : sged 

Optimal Parameters
------------------------------------
        Estimate  Std. Error   t value Pr(>|t|)
mu      0.000431    0.000233    1.8518 0.064053
ar1     0.189335    0.011645   16.2586 0.000000
ar2    -0.781756    0.006700 -116.6736 0.000000
ar3    -0.378325    0.011873  -31.8647 0.000000
ma1    -0.145958    0.002124  -68.7036 0.000000
ma2     0.760576    0.000178 4262.1596 0.000000
ma3     0.420458    0.000199 2112.7758 0.000000
omega   0.000002    0.000002    0.8715 0.383483
alpha1  0.048260    0.023036    2.0950 0.036173
beta1   0.933232    0.027814   33.5526 0.000000
skew    0.974339    0.027399   35.5617 0.000000
shape   1.327237    0.057339   23.1471 0.000000

Robust Standard Errors:
        Estimate  Std. Error    t value Pr(>|t|)
mu      0.000431    0.000319   1.353063 0.176035
ar1     0.189335    0.103649   1.826699 0.067745
ar2    -0.781756    0.062726 -12.463018 0.000000
ar3    -0.378325    0.101064  -3.743410 0.000182
ma1    -0.145958    0.015931  -9.162173 0.000000
ma2     0.760576    0.001570 484.420406 0.000000
ma3     0.420458    0.001675 251.046693 0.000000
omega   0.000002    0.000027   0.081055 0.935398
alpha1  0.048260    0.218252   0.221122 0.824998
beta1   0.933232    0.277155   3.367183 0.000759
skew    0.974339    0.157307   6.193848 0.000000
shape   1.327237    0.472835   2.806979 0.005001

LogLikelihood : 6436.01 

Information Criteria
------------------------------------
                    
Akaike       -6.3541
Bayes        -6.3208
Shibata      -6.3542
Hannan-Quinn -6.3419

Weighted Ljung-Box Test on Standardized Residuals
------------------------------------
                         statistic p-value
Lag[1]                      0.4759  0.4903
Lag[2*(p+q)+(p+q)-1][17]    1.8620  1.0000
Lag[4*(p+q)+(p+q)-1][29]    5.2499  1.0000
d.o.f=6
H0 : No serial correlation

Weighted Ljung-Box Test on Standardized Squared Residuals
------------------------------------
                        statistic p-value
Lag[1]                     0.4092  0.5224
Lag[2*(p+q)+(p+q)-1][5]    0.6169  0.9382
Lag[4*(p+q)+(p+q)-1][9]    0.7745  0.9937
d.o.f=2

Weighted ARCH LM Tests
------------------------------------
            Statistic Shape Scale P-Value
ARCH Lag[3]    0.1876 0.500 2.000  0.6649
ARCH Lag[5]    0.3232 1.440 1.667  0.9340
ARCH Lag[7]    0.4031 2.315 1.543  0.9863

Nyblom stability test
------------------------------------
Joint Statistic:  76.8199
Individual Statistics:              
mu     0.20597
ar1    0.05513
ar2    0.12936
ar3    0.13974
ma1    0.11222
ma2    0.03197
ma3    0.13386
omega  2.28167
alpha1 0.47662
beta1  0.65528
skew   0.04106
shape  0.08178

Asymptotic Critical Values (10% 5% 1%)
Joint Statistic:         2.69 2.96 3.51
Individual Statistic:    0.35 0.47 0.75

Sign Bias Test
------------------------------------
                   t-value   prob sig
Sign Bias           0.7525 0.4518    
Negative Sign Bias  0.1022 0.9186    
Positive Sign Bias  0.2840 0.7764    
Joint Effect        1.6855 0.6402    


Adjusted Pearson Goodness-of-Fit Test:
------------------------------------
  group statistic p-value(g-1)
1    20     40.12     0.003159
2    30     46.34     0.021710
3    40     55.11     0.045169
4    50     66.13     0.051801


Elapsed time : 3.653 
#plot(fit)
resid <- residuals(fit, standardize = TRUE)
Acf(resid)

Pacf(resid)

v33 <- sqrt(252) * fit@fit$sigma*100
head(v33)
[1] 17.27730 17.27730 17.27730 16.85526 16.52336 17.37468
plot(sqrt(252) * fit@fit$sigma, type='l')

plot(fit, which = 1)

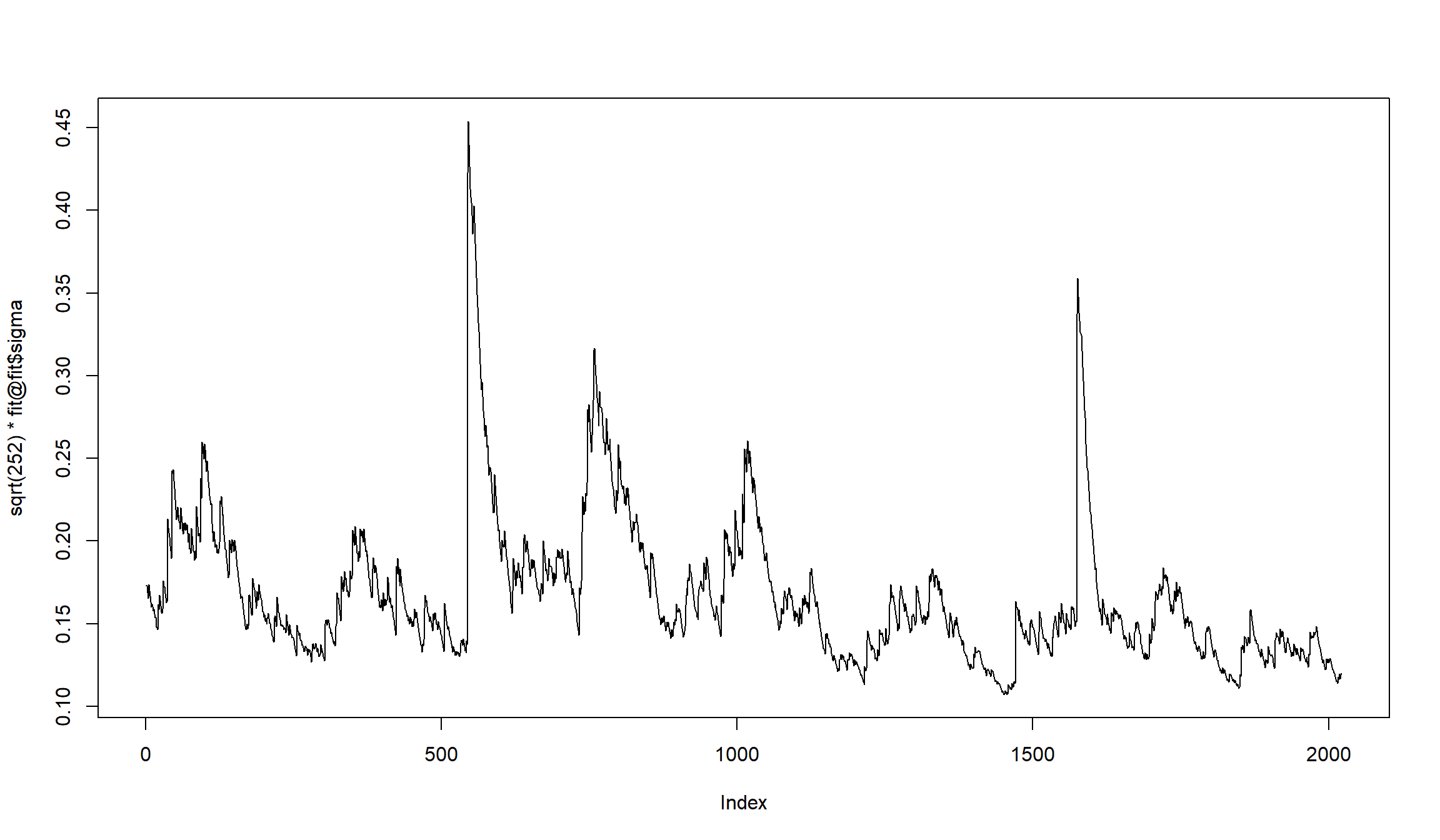
Сравнение оценок GARCH разных моделей среднего

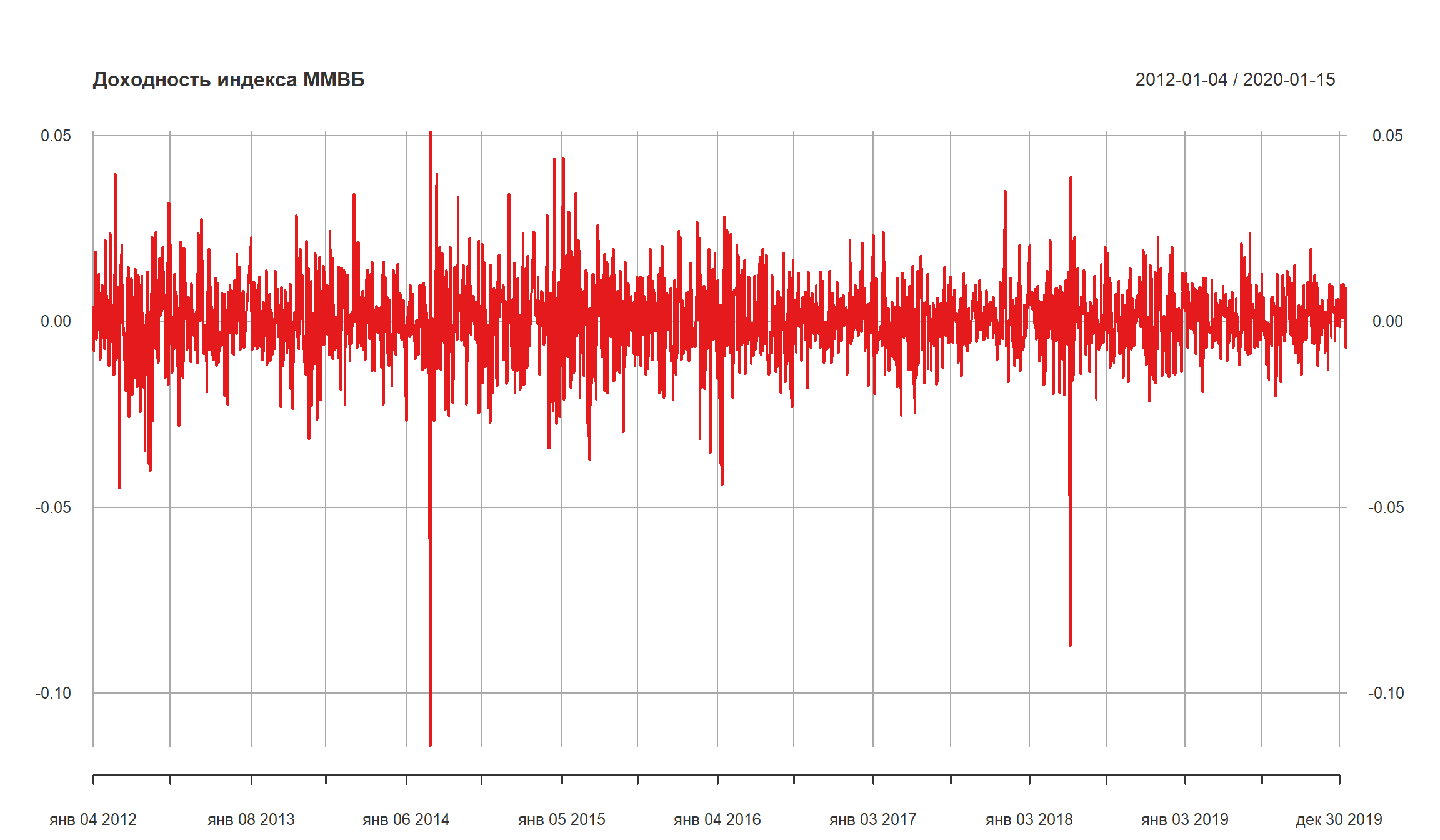
сравним оценку волатильности доходностей индекс ММВБ двух разных моделей:

  1. GARCH(1,1) + константа для доходностей
  2. GARCH(1,1)+ARMA(3,3)
plot(index(MICEX.rtn),v11,type="l",col="red", xlab= 'год', ylab = '% ujl')
Error in xy.coords(x, y, xlabel, ylabel, log): 'x' and 'y' lengths differ
lines(index(MICEX.rtn),v33,col="green")
Error in plot.xy(xy.coords(x, y), type = type, ...): plot.new has not been called yet

Оценки модели очень близки друг к другу.

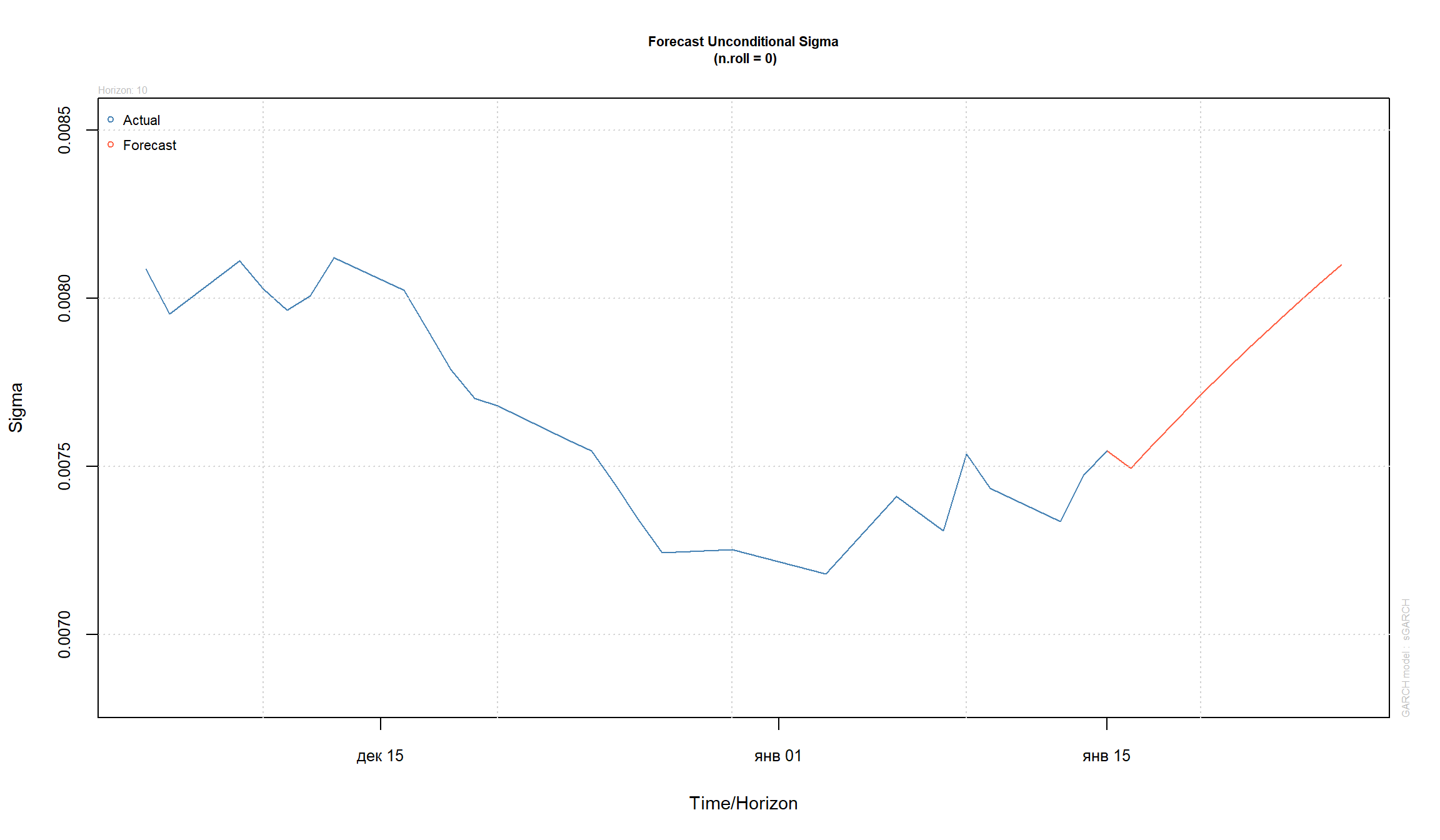
Прогнозирование с помощью GARCH

GARCH модели позволяют строить прогнозы исходной серии и прогнозы для волатильности:

fcst = ugarchforecast(fit, n.ahead=10)
plot(fcst, which = 1) # прогноз для ряда

plot(fcst, which = 3) # прогноз для волатильности

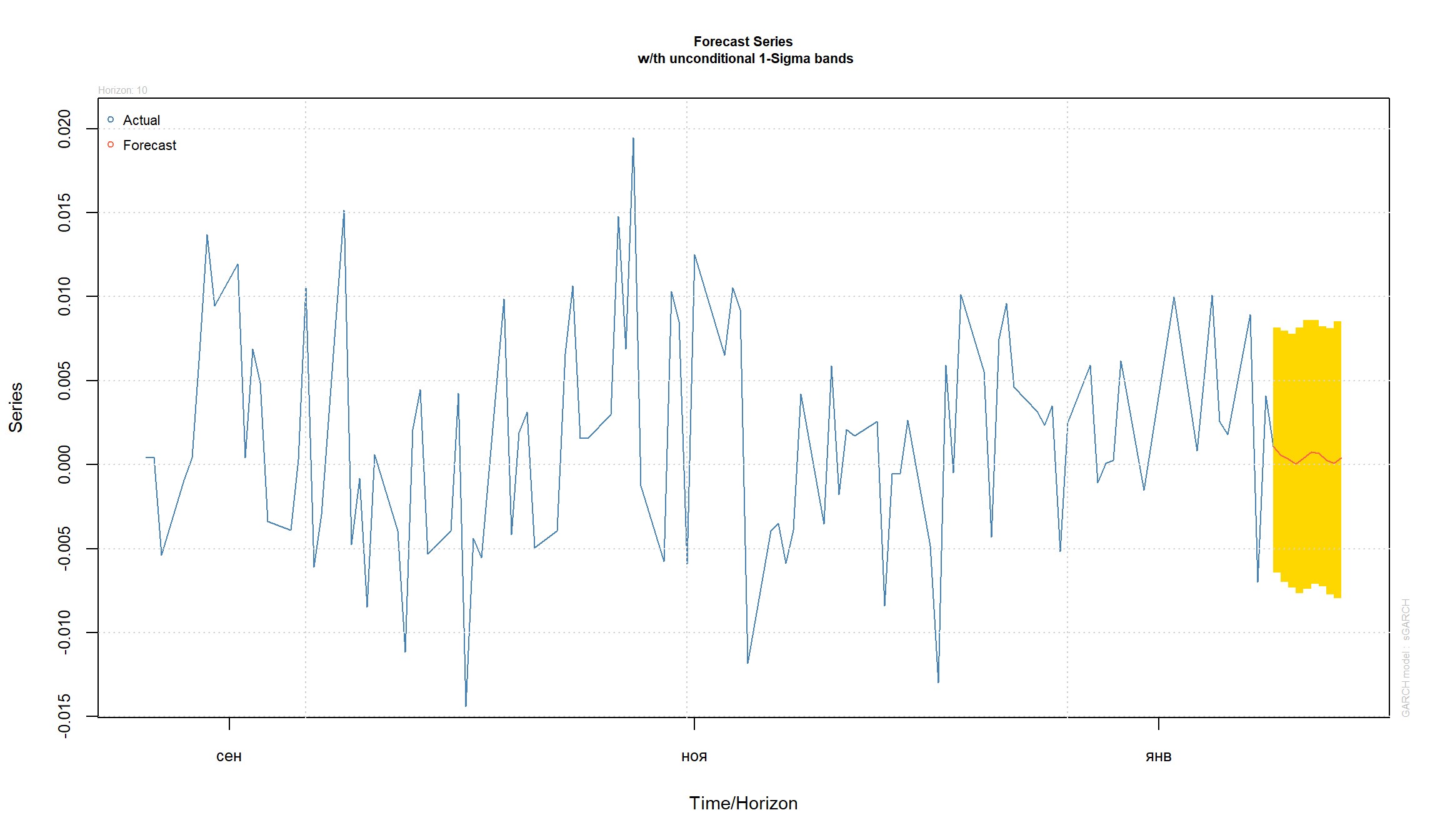
Использованные источники:

  1. “An Introduction to Analysis of Financial Data with R” (Ruey S. Tsay)
  2. “Statistics and Data Analysis for Financial Engineering” (David Ruppert & David Matteson)
  3. Analyzing Financial Data and Implementing Financial Models Using R (Clifford Ang)
  4. Forecasting Financial Time Series (Patrick Perry)
  5. Generalised Autoregressive Conditional Heteroskedasticity GARCH(p, q) Models for Time Series Analysis (Michael Halls-Moore)